
Definice a vzorce průměrné úhlové rychlosti, řešená cvičení
The střední úhlová rychlost Rotace je definována jako úhel natočený za jednotku času vektoru polohy bodu, který popisuje kruhový pohyb. Lopatky stropního ventilátoru (jako na obrázku 1) sledují kruhový pohyb a jejich průměrná úhlová rychlost otáčení se vypočítá z kvocientu mezi natočeným úhlem a časem, ve kterém byl tento úhel posunut..
Pravidla, kterými se rotační pohyb řídí, jsou poněkud podobná pravidlům pro translační pohyb. Ujeté vzdálenosti lze měřit také v metrech, avšak úhlové velikosti mají zvláštní význam, protože značně usnadňují popis pohybu.
Obecně se pro úhlové veličiny používají řecká písmena a pro lineární veličiny latinská písmena..
Rejstřík článků
- 1 Definice a vzorce
- 1.1 Rovnoměrné otáčení
- 2 Vyřešená cvičení
- 2.1 - Cvičení 1
- 2.2 - Cvičení 2
- 3 Odkazy
Definice a vzorce
Obrázek 2 představuje pohyb bodu po kruhové dráze c. Poloha P bodu odpovídá okamžiku t a úhlová poloha odpovídající tomuto okamžiku je is.
Od okamžiku t uplyne časové období Δt. V tomto období je nová poloha bodu P 'a úhlová poloha se zvýšila o úhel Δϕ.
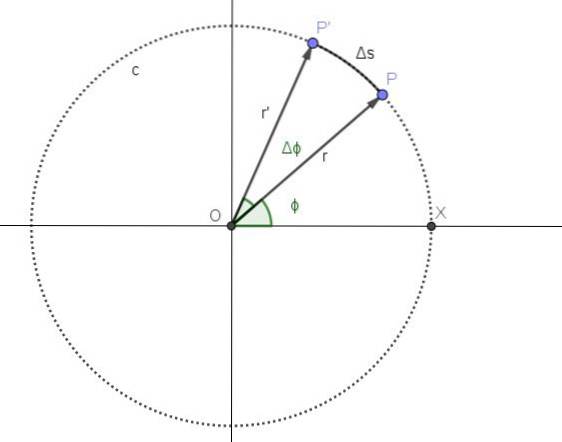
Střední úhlová rychlost ω je úhel uražený za jednotku času, takže kvocient Δϕ / Δt bude představovat střední úhlovou rychlost mezi časy t at + Δt:
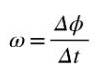
Protože úhel se měří v radiánech a čas v sekundách, jednotka pro střední úhlovou rychlost je rad / s. Pokud chcete vypočítat úhlová rychlost hned v okamžiku t, pak budeme muset vypočítat kvocient Δϕ / Δt, když Δt ➡0.

Rovnoměrné otáčení
Rotační pohyb je rovnoměrný, pokud v kterémkoli pozorovaném okamžiku je uhelný úhel stejný ve stejném časovém období. Pokud je rotace rovnoměrná, pak se úhlová rychlost v kterémkoli okamžiku shoduje se střední úhlovou rychlostí.
V jednotném rotačním pohybu se čas, ve kterém je provedena jedna úplná revoluce, nazývá doba a je označen T.
Kromě toho, když je provedeno úplné otočení, je cestovní úhel 2π, takže při rovnoměrné rotaci je úhlová rychlost ω vztažena k periodě T, podle následujícího vzorce:
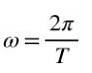
Definuje frekvence F rovnoměrné rotace jako kvocient mezi počtem závitů a časem použitým k jejich průchodu, tj. pokud se v časovém období Δt provede N závitů, pak bude frekvence:
f = N / Δt
Vzhledem k tomu, že jedna odbočka (N = 1) je projetá v čase T (období), získá se následující vztah:
f = 1 / T.
To znamená, že při rovnoměrné rotaci úhlová rychlost souvisí s frekvencí prostřednictvím vztahu:
ω = 2π ・ f
Vztah mezi úhlovou rychlostí a lineární rychlostí
Lineární rychlost proti, je podíl mezi ujetou vzdáleností a časem potřebným k jejímu ujetí. Na obrázku 2 je uražená vzdálenost délkou oblouku Δs.
Oblouk Δs je úměrný uhlovému úhlu Δϕ a poloměru r, přičemž je splněn následující vztah:
Δs = r ・ Δϕ
Dokud se Δϕ měří v radiánech.
Vydělíme-li předchozí výraz časovou prodlevou Δt, získáme:
(Δs / Δt) = r ・ (Δϕ / Δt)
Kvocient prvního prvku je lineární rychlost a kvocient druhého prvku je střední úhlová rychlost:
v = r ・ ω
Vyřešená cvičení
-Cvičení 1
Konce lopatek stropního ventilátoru zobrazené na obrázku 1 se pohybují rychlostí 5 m / s a lopatky mají poloměr 40 cm.
S těmito údaji vypočítejte: i) průměrnou úhlovou rychlost kola, ii) počet otáček, které kolo provede za jednu sekundu, iii) období v sekundách.
Řešení
i) Lineární rychlost je v = 5 m / s.
Poloměr je r = 0,40 m.
Ze vztahu mezi lineární rychlostí a úhlovou rychlostí řešíme druhou:
v = r ・ ω => ω = v / r = (5 m / s) / (0,40 m) = 12,57 rad / s
ii) ω = 2π ・ f => f = ω / 2π = (12,57 rad / s) / (2π rad) = 2 otáčky / s
iii) T = 1 / f = 1 / (2 otáčky / s) = 0,5 s pro každé kolo.
-Cvičení 2
Hračkový kočárek se pohybuje po kruhové dráze s poloměrem 2 m. Za 0 s je jeho úhlová poloha 0 rad, ale po čase t je jeho úhlová poloha
φ (t) = 2 ・ t .
S těmito daty
i) Vypočítejte průměrnou úhlovou rychlost v následujících časových intervalech [0 s, 0,5 s]; [0,5 s, 1,0 s]; [1,0 s, 1,5 s] a nakonec v období [0,0 s, 1,5 s].
ii) Na základě výsledků části i) Co lze říci o pohybu?
iii) Určete střední lineární rychlost ve stejném časovém období z části i)
iv) Najděte úhlovou rychlost a lineární rychlost pro jakýkoli okamžik.
Řešení
i) Střední úhlová rychlost je dána následujícím vzorcem:
Pokračujeme v výpočtu uraženého úhlu a uplynulého času v každém intervalu.
Interval 1: Δϕ = ϕ (0,5 s) - ϕ (0,0 s) = 2 (rad / s) * 0,5 s - 2 (rad / s) * 0,0 s = 1,0 rad
Δt = 0,5 s - 0,0 s = 0,5 s
ω = Δϕ / Δt = 1,0rad / 0,5s = 2,0 rad / s
Interval 2: Δϕ = ϕ (1,0 s) - ϕ (0,5 s) = 2 (rad / s) * 1,0 s - 2 (rad / s) * 0,5 s = 1,0 rad
Δt = 1,0 s - 0,5 s = 0,5 s
ω = Δϕ / Δt = 1,0rad / 0,5s = 2,0 rad / s
Interval 3: Δϕ = ϕ (1,5 s) - ϕ (1,0 s) = 2 (rad / s) * 1,5 s - 2 (rad / s) * 1,0 s = 1,0 rad
Δt = 1,5 s - 1,0 s = 0,5 s
ω = Δϕ / Δt = 1,0rad / 0,5s = 2,0 rad / s
Interval 4: Δϕ = ϕ (1,5 s) - ϕ (0,0 s) = 2 (rad / s) * 1,5 s - 2 (rad / s) * 0,0 s = 3,0 rad
Δt = 1,5 s - 0,0 s = 1,5 s
ω = Δϕ / Δt = 3,0rad / 1,5s = 2,0 rad / s
ii) S ohledem na předchozí výsledky, ve kterých byla průměrná úhlová rychlost vypočítána v různých časových intervalech, přičemž se vždy získal stejný výsledek, se zdá, že to naznačuje jednotný kruhový pohyb. Tyto výsledky však nejsou přesvědčivé..
Způsob, jak zajistit závěr, je výpočet střední úhlové rychlosti pro libovolný interval [t, t ']: Δϕ = ϕ (t') - ϕ (t) = 2 * t '- 2 * t = 2 * (t '-t)
Δt = t '- t
ω = Δϕ / Δt = 2 * (t'-t) / (t'-t) = 2,0 rad / s
To znamená, že kočárek má konstantní střední úhlovou rychlost 2 rad / s v jakémkoli uvažovaném časovém období. Ale můžete jít dále, pokud vypočítáte okamžitou úhlovou rychlost:
To se interpretuje tak, že autíčko má po celou dobu konstantní úhlovou rychlost = 2 rad / s.
Reference
- Giancoli, D. Fyzika. Zásady s aplikacemi. 6. vydání. Prentice Hall. 30-45.
- Kirkpatrick, L. 2007. Fyzika: Pohled na svět. 6ta Zkrácené vydání. Cengage Learning. 117.
- Resnick, R. (1999). Fyzický. Svazek 1. Třetí vydání ve španělštině. Mexiko. Compañía Editorial Continental S.A. de C.V. 33-52.
- Serway, R., Jewett, J. (2008). Fyzika pro vědu a techniku. Svazek 1. 7. Edice. Mexiko. Cengage Learning Editors. 32-55.
- Wikipedia. Úhlová rychlost. Obnoveno z: wikipedia.com


Zatím žádné komentáře