Okamžitá definice rychlosti, vzorec, výpočet a cvičení

The okamžitá rychlost je definována jako okamžitá změna posunu v čase. Jedná se o koncept, který studiu pohybu dodává velkou přesnost. A je to pokrok s ohledem na průměrnou rychlost, jejíž informace jsou velmi obecné.

Abychom získali okamžitou rychlost, podívejme se na co nejmenší časový interval. Diferenciální počet je dokonalým nástrojem k vyjádření této myšlenky matematicky.

Výchozím bodem je průměrná rychlost:

Tento limit se nazývá derivát. V notaci diferenciálního počtu máme:

Kdykoli je pohyb omezen na přímku, od vektorového zápisu lze upustit.

Rejstřík článků

• 1 Výpočet okamžité rychlosti: geometrická interpretace
• 2 Některé speciální případy při výpočtu okamžité rychlosti
• 3 Vyřešená cvičení okamžité rychlosti
  • 3.1 Cvičení 1
  • 3.2 Cvičení 2
• 4 Odkazy

Výpočet okamžité rychlosti: geometrická interpretace

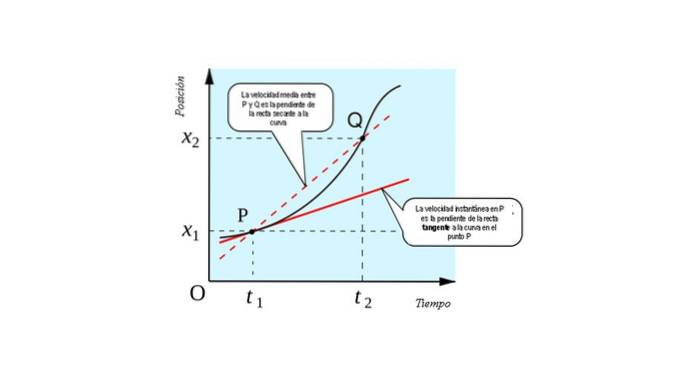
Následující obrázek ukazuje geometrickou interpretaci derivačního konceptu: je to sklon přímky tečna na křivku x (t) vs. t v každém bodě.

Dokážete si představit, jak dosáhnout limitu, pokud se k bodu Q přiblíží kousek po kousku do P. Přijde čas, kdy jsou oba body tak blízko, že nebudete schopni rozlišit jeden od druhého..

Přímka, která je spojuje, poté přejde od sečny (přímka, která se protíná ve dvou bodech), až po tečnu (přímka, která se dotkne křivky pouze v jednom bodě). Abychom tedy našli okamžitou rychlost pohybující se částice, měli bychom mít:

• Graf polohy částice jako funkce času. Když najdeme sklon tečny ke křivce v každém okamžiku, máme okamžitou rychlost v každém bodě, který částice zaujímá.

Dobře:

• Funkce polohy částic x (t), který je odvozen k získání funkce rychlosti v (t), pak je tato funkce vyhodnocena v každém taktu t, v pohodlí. Předpokládá se, že poziční funkce je diferencovatelná.

Některé speciální případy při výpočtu okamžité rychlosti

-Sklon tečny ke křivce v P je 0. Nulový sklon znamená, že mobilní zařízení je nehybné a že jeho rychlost je samozřejmě 0.

-Sklon přímky tečné ke křivce v bodě P je větší než 0. Rychlost je kladná. Ve výše uvedeném grafu to znamená, že se mobilní zařízení pohybuje od O.

-Sklon tečny ke křivce v P je menší než 0. Rychlost by byla záporná. Ve výše uvedeném grafu nejsou žádné takové body, ale v tomto případě by se částice blížila k O.

-Sklon přímky tečné ke křivce je konstantní v P a ve všech ostatních bodech. V tomto případě je graf přímka a mobil má rovnoměrný pohyb čáry MRU (jeho rychlost je konstantní).

Obecně platí, že funkce v (t) je to také funkce času, který může mít derivaci. Co kdyby nebylo možné najít derivace funkcí x (t) Y v (t)?

V případě x (t) mohlo by se stát, že sklon - okamžitá rychlost - se náhle změní. Nebo že by to okamžitě šlo z nuly na jinou hodnotu.

Pokud ano, graf x (t) představovalo by to body nebo rohy v místech náhlých změn. Velmi odlišné od případu znázorněného na předchozím obrázku, ve kterém je křivka x (t) je hladká křivka bez bodů, rohů, nespojitostí nebo náhlých změn.

Pravdou je, že pro skutečné mobily jsou hladké křivky ty, které nejlépe reprezentují chování objektu.

Pohyb je obecně poměrně složitý. Mobily lze na chvíli zastavit, zrychlit, přejít z klidu, mít rychlost a odejít z výchozího bodu, chvíli udržovat rychlost, poté brzdit, aby se znovu zastavilo atd..

Opět mohou začít znovu a pokračovat stejným směrem. Nebo aktivujte zpátečku a zpátečku. Tomu se říká různorodý pohyb v jedné dimenzi..

Zde je několik příkladů výpočtu okamžité rychlosti, které objasní použití uvedených definic:

Vyřešená cvičení okamžité rychlosti

Cvičení 1

Částice se pohybuje po přímce s následujícím zákonem pohybu:

x (t) = -t³ + 2 t^dva + 6 t - 10

Všechny jednotky jsou v mezinárodním systému. Nalézt:

a) Poloha částice v t = 3 sekundy.

b) Průměrná rychlost v intervalu mezi t = 0 sa t = 3 s.

c) Průměrná rychlost v intervalu mezi t = 0 sa t = 3 s.

d) Okamžitá rychlost částice z předchozí otázky, při t = 1 s.

Odpovědi

a) Chcete-li zjistit polohu částice, vyhodnotí se zákon pohybu (funkce polohy) při t = 3:

x (3) = (-4/3) .3³ + 2. 3^dva ₊ 6,3 - 10 m = -10 m

Není problém, že pozice je negativní. Znaménko (-) označuje, že částice je nalevo od počátku O.

b) Při výpočtu průměrné rychlosti jsou v uvedených časech požadovány konečné a počáteční polohy částice: x (3) a x (0). Pozice v t = 3 je x (3) a je známa z předchozího výsledku. Pozice v t = 0 sekund je x (0) = -10 m.

Vzhledem k tomu, že konečná poloha je stejná jako počáteční poloha, je okamžitě uzavřeno, že průměrná rychlost je 0.

c) Průměrná rychlost je poměr mezi ujetou vzdáleností a časem. Nyní je vzdálenost modulem nebo velikostí posunutí, proto:

vzdálenost = | x2 - x1 | = | -10 - (-10) | m = 20 m

Uvědomte si, že ujetá vzdálenost je vždy pozitivní.

proti_{m = 20 m / 3 s = 6,7 m / s}

d) Zde je nutné najít první derivaci polohy s ohledem na čas. Poté se vyhodnotí na t = 1 sekundu.

x '(t) = -4 t^dva + 4 t + 6

x '(1) = -4,1^dva + 4,1 + 6 m / s = 6 m / s

Cvičení 2

Níže je uveden graf polohy mobilního telefonu jako funkce času. Najděte okamžitou rychlost t = 2 sekundy.

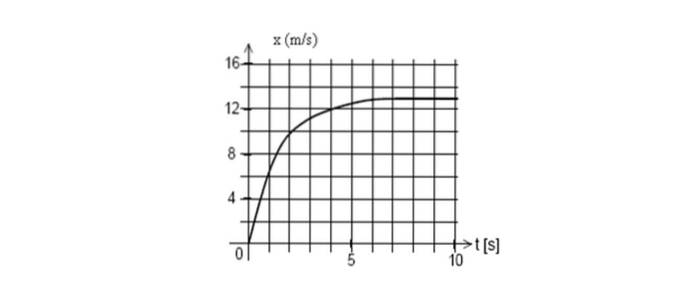
Odpovědět

Nakreslete tečnou přímku ke křivce v t = 2 sekundy, poté vypočítejte její sklon a vezměte libovolné dva body na přímce.

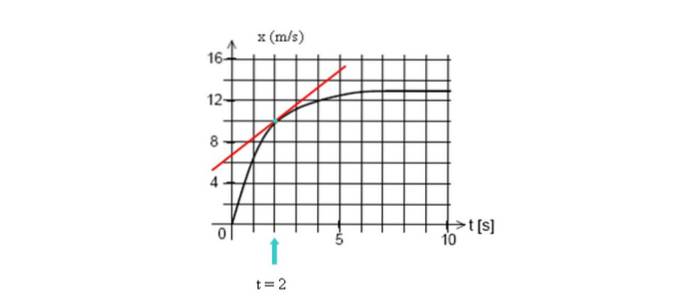
V tomto příkladu vezmeme dva snadno vizualizovatelné body, jejichž souřadnice jsou (2 s, 10 m) a řez svislou osou (0 s, 7 m):

Reference

1. Giancoli, D. Fyzika. Zásady s aplikacemi. 6^th Edice. Prentice Hall. 22-25.
2. Resnick, R. (1999). Fyzický. Svazek 1. Třetí vydání ve španělštině. Mexiko. Compañía Editorial Continental S.A. de C.V. 21-22.
3. Serway, R., Jewett, J. (2008). Fyzika pro vědu a techniku. Svazek 1. 7^ma. Edice. Mexiko. Cengage Learning Editors. 23-25.