The multiplikativní problémy Učí se dětem na základní škole, poté, co se dozvěděli fakta o sčítání a odčítání, nazývaná také sčítání a odčítání..
Je důležité naučit děti, že násobení celých čísel je opravdu součet, ale je nezbytné naučit se násobit, aby se tyto sčítání dělaly rychleji a snadněji.
Je nezbytné si dobře vybrat první problémy, které se použijí k tomu, aby se děti naučily množit, protože to musí být problémy, kterým mohou rozumět a vidí užitečnost učení se množit.
Nestačí je jednoduše naučit násobilky mechanicky, je mnohem atraktivnější ukázat jim jejich použití v situacích, které vznikají v každodenním životě, například když jejich rodiče jdou nakupovat.
Existuje mnoho problémů, které lze použít k tomu, aby se dítě naučilo používat tabulky násobení, níže uvádíme některé problémy s jejich řešením.
Knihovník musí třídit knihy na policích knihovny. Na konci pátečního odpoledne si knihovník uvědomí, že ještě musí objednat 78 krabic knih, z nichž každá má 5 knih. Kolik knih bude knihovník muset objednat příští týden?
Řešení: V tomto problému je třeba poznamenat, že všechny krabice mají stejný počet knih. Proto 1 rámeček představuje 5 knih, 2 rámečky představují 5 + 5 = 10 knih, 3 rámečky představují 5 + 5 + 5 = 15 knih. Ale dělat všechny tyto částky je velmi rozsáhlý proces.
Provedení všech výše uvedených částek se rovná vynásobení počtu knih v každé krabici počtem krabic zbývajících k objednání. A to, 5 × 78, proto musí knihovník objednat 390 knihy.
Zemědělec musí zabalit kávu získanou při své poslední sklizni do krabic. Celková sklizeň je 20 000 kilogramů a krabice, do kterých je budete balit, mají maximální kapacitu 100 kilogramů. Kolik krabic potřebuje zemědělec k zabalení celé sklizně?
Řešení: První věc, kterou si všimnete, je, že všechny krabice mají stejnou kapacitu (100 kilogramů). Pokud tedy zemědělec používá 2 krabice, může zabalit pouze 100 + 100 = 200 kilogramů. Pokud použijete 4 krabice, zabalíte 200 + 200 = 400 kilogramů.
Stejně jako dříve je celé toto přidání navíc velmi dlouhý proces. Klíčem je najít číslo, které po vynásobení 100 znamená výsledek 20 000.
Při podrobném zkoumání je vidět, že toto číslo je 200, protože 200 × 100 = 20 000.
Zemědělec proto potřebuje 200 krabic, aby zabalil celou sklizeň..
Maria se právě nastěhovala do budovy a chtěla by vědět, kolik oken má budova na přední straně. Budova má 13 pater a na každém patře jsou 3 okna.
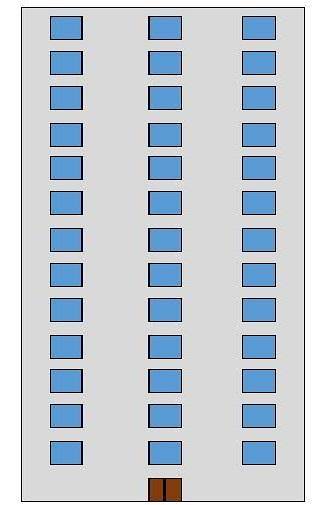
Řešení: v tomto problému můžete spočítat počet oken podlahu a přidat je, abyste získali odpověď.
Ale protože každé patro má stejný počet oken, je mnohem rychlejší vynásobit počet podlaží počtem oken v každém patře. To znamená, 13 × 3, proto má budova 39 oken.
Javier je zedník, který staví podlahu v koupelně. Javier zatím umístil 9 dlaždic (čtverců) na podlahu koupelny, jak je znázorněno na obrázku níže. Kolik dlaždic je potřeba k pokrytí celé podlahy koupelny?
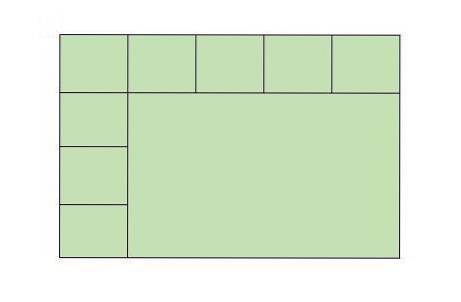
Řešení- Jedním ze způsobů, jak tento problém vyřešit, je dokončení vyplňování obrázku nakreslením chybějících dlaždic a jejich následným počítáním.
Podle obrázku se ale na podlahu koupelny vejde 5 dlaždic horizontálně a 4 vertikálně. Celá podlaha koupelny proto bude mít celkem 5 × 4 = 20 dlaždic.
Měsíce leden, březen, květen, červenec, srpen, říjen a prosinec mají vždy 31 dnů. Jaký je celkový počet dní, které se sečtou všechny tyto měsíce??
Řešení: v tomto cvičení jsou výslovně uvedeny údaje, což je počet dní (31). Druhé údaje jsou uvedeny implicitně v měsících (7). Celkový počet dní mezi všemi těmito měsíci je tedy 7 × 31 = 217.
Zatím žádné komentáře