Gravitační zrychlení, co to je, jak se měří a cvičení

The gravitační zrychlení nebo gravitační zrychlení je definováno jako intenzita gravitačního pole Země. To znamená, že síla, kterou působí na jakýkoli objekt, na jednotku hmotnosti.

Označuje se nyní známým písmenem g a jeho přibližná hodnota v blízkosti zemského povrchu je 9,8 m / s^dva. Tato hodnota může zaznamenat malé odchylky s geografickou šířkou a také s výškou vzhledem k hladině moře..

Gravitační zrychlení má kromě výše uvedené velikosti také směr a smysl. Ve skutečnosti je směrován svisle ke středu Země.

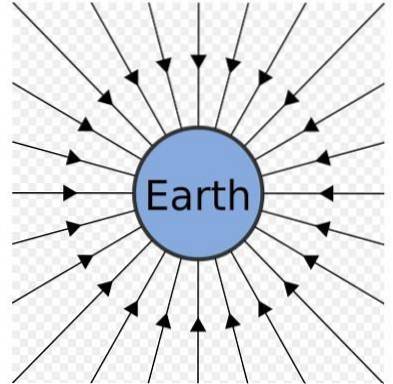
Gravitační pole Země může být reprezentováno jako sada radiálních čar, které směřují ke středu, jak je znázorněno na předchozím obrázku.

Rejstřík článků

• 1 Co je gravitační zrychlení?
  • 1.1 Zákon univerzální gravitace
• 2 Jak se měří gravitace na různých planetách?
  • 2.1 Experiment ke stanovení hodnoty g
  • 2.2 Standardní hodnota g na Zemi, na Měsíci a na Marsu
  • 2.3 Gravitace na Měsíci
  • 2.4 Gravitace na Marsu
• 3 Cvičení vyřešeno: padající jablko
• 4 Odkazy

Co je gravitační zrychlení?

Hodnota gravitačního zrychlení na Zemi nebo na jakékoli jiné planetě je ekvivalentní intenzitě gravitačního pole, které produkuje a které nezávisí na objektech kolem, ale pouze na jeho vlastní hmotnosti a poloměru..

Gravitační zrychlení je často definováno jako zrychlení, které zažívá jakýkoli objekt při volném pádu v blízkosti zemského povrchu..

V praxi k tomu téměř vždy dochází, jak uvidíme v následujících částech, ve kterých bude použit Newtonův zákon univerzální gravitace..

Newton prý objevil tento slavný zákon při meditaci o padajících tělech pod strom. Když ucítil úder jablka na hlavu, okamžitě věděl, že síla, díky níž jablko padá, je stejná, jako když Měsíc obíhá kolem Země..

Zákon univerzální gravitace

Ať už byla legenda o jablku pravdivá nebo ne, Newton si uvědomil, že velikost gravitační síly přitažlivosti mezi jakýmikoli dvěma objekty, například mezi Zemí a Měsícem nebo Zemí a jablkem, musí záviset na jejich hmotách:

Charakteristiky gravitační síly

Gravitační síla je vždy atraktivní; to znamená, že dvě těla, která ovlivňuje, se navzájem přitahují. Opak není možný, protože dráhy nebeských těles jsou uzavřené nebo otevřené (například komety) a odpudivá síla nemůže nikdy vytvořit uzavřenou dráhu. Takže masy vždy přitahují, ať už se děje cokoli.

Poměrně dobrá aproximace skutečného tvaru Země (m₁) A Měsíce nebo jablka (m_dva) předpokládá, že mají sférický tvar. Následující obrázek představuje tento jev.

Zde obě síly působily m₁ Asi m_dva, jako ten, který m_dva Asi m₁, oba stejné velikosti a směřující podél čáry, která spojuje středy. Nejsou zrušeny, protože jsou použity na různé objekty.

Ve všech následujících částech se předpokládá, že objekty jsou homogenní a sférické, proto se jejich těžiště shoduje s jejich geometrickým středem. Lze předpokládat, že veškerá hmota je soustředěna právě tam.

Jak měříte gravitaci na různých planetách?

Gravitaci lze měřit pomocí gravimetru, gravitačního měřicího zařízení používaného při geofyzikálních gravimetrických průzkumech. V současné době jsou mnohem propracovanější než originály, ale zpočátku vycházely z kyvadla.

Kyvadlo se skládá z tenkého, lehkého a neroztažitelného lana o délce L. Jeden z jeho konců je připevněn k podpěře a hmota m je zavěšena za druhý..

Když je systém v rovnováze, hmota visí svisle, ale když je od ní oddělena, začne oscilovat a provádí pohyb tam a zpět. Gravitace je za to zodpovědná. Ze všeho, co následuje, lze předpokládat, že gravitace je jedinou silou působící na kyvadlo.

Perioda T oscilace kyvadla pro malé oscilace je dána následující rovnicí:

Experiment k určení hodnoty G

Materiály

- 1 kovová koule.

- Lano několika různých délek, nejméně 5.

- Měřicí páska.

- Dopravník.

- Chronometr.

- Držák pro upevnění kyvadla.

- Milimetrový papír nebo počítačový program s tabulkou.

Proces

1. Vyberte jeden z řetězců a sestavte kyvadlo. Změřte délku řetězce + poloměr koule. To bude délka L.
2. Sejměte kyvadlo z rovnovážné polohy asi o 5 stupňů (změřte jej úhloměrem) a nechejte jej houpat.
3. Současně spusťte stopky a změřte čas 10 oscilací. Zapište si výsledek.
4. Výše uvedený postup opakujte pro ostatní délky.
5. Najděte čas, za který se kyvadlo otočí (vydělte každý z výše uvedených výsledků 10).
6. Každá získaná hodnota se umocňuje na druhou, přičemž se získá T^dva
7. Na milimetrový papír zakreslete každou hodnotu T do grafu^dva na svislé ose proti příslušné hodnotě L na vodorovné ose. Buďte v souladu s jednotkami a nezapomeňte vzít v úvahu chybu při hodnocení použitých nástrojů: měřicí páska a stopky..
8. Nakreslete nejlepší čáru, která odpovídá vykresleným bodům.
9. Najděte sklon m uvedené linie pomocí dvou bodů, které k ní patří (ne nutně experimentální body). Přidejte experimentální chybu.
10. Výše uvedené kroky lze provést pomocí tabulky a možnosti sestavit a přizpůsobit přímku.
11. Z hodnoty sklonu na vymazat hodnotu G s příslušnou experimentální nejistotou.

Standardní hodnota G na Zemi, na Měsíci a na Marsu

Standardní hodnota gravitace na Zemi je: 9,81 m / s^dva, na 45 ° severní šířky a na úrovni moře. Protože Země není dokonalá sféra, hodnoty G mírně se liší, je vyšší na pólech a nižší na rovníku.

Ti, kteří chtějí znát hodnotu ve své lokalitě, ji najdou aktualizovanou na webových stránkách Německého metrologického institutu PTB (Physikalisch-Technische Bundesanstalt), v části Gravitační informační systém (KŘÍDA).

Gravitace na Měsíci

Gravitační pole Měsíce bylo určeno analýzou rádiových signálů z vesmírných sond obíhajících kolem satelitu. Jeho hodnota na měsíčním povrchu je 1,62 m / s^dva

Gravitace na Marsu

Hodnota G_P pro planetu záleží na její hmotnosti M a jejím poloměru R takto:

Proto:

U planety Mars jsou k dispozici následující údaje:

M = 6,4 185 x 10^{2. 3} kg

R = 3390 km

G = 6,67 x 10^-jedenáct N.m^dva/ kg^dva

S těmito údaji víme, že gravitace Marsu je 3,71 m / s^dva. Stejnou rovnici lze přirozeně použít s údaji o Měsíci nebo jiné planetě, a tak odhadnout hodnotu její gravitace.

Cvičení vyřešeno: padající jablko

Předpokládejme, že Země i jablko mají kulatý tvar. Hmotnost Země je M = 5,98 x 10²⁴ kg a jeho poloměr je R = 6,37 x 10⁶  m. Hmotnost jablka je m = 0,10 kg. Předpokládejme, že kromě gravitace neexistuje žádná jiná síla. Z Newtonova zákona univerzální gravitace najdete:

a) Gravitační síla, kterou Země vyvíjí na jablko.

b) Zrychlení, které zažívá jablko, když je uvolněno z určité výšky, podle Newtonova druhého zákona.

Řešení

a) Jablko (údajně sférické, podobně jako Země) má ve srovnání s poloměrem Země velmi malý poloměr a je ponořeno do svého gravitačního pole. Následující obrázek zjevně není v měřítku, ale existuje schéma gravitačního pole G, a sílu F vynaložené zemí na jablko:

Použitím Newtonova zákona univerzální gravitace lze vzdálenost mezi středy považovat za zhruba stejnou hodnotu jako poloměr Země (výška, ze které jablko padá, je také zanedbatelná ve srovnání s poloměrem Země). Proto:

b) Podle druhého Newtonova zákona je velikost síly působící na jablko:

F = ma = mg

Jeho hodnota je podle předchozího výpočtu 0,983 N. Vyrovnáme-li obě hodnoty a poté vyřešíme velikost zrychlení, získáme:

mg = 0,983 N

g = 0,983 N / 0,10 kg = 9,83 m / s^dva

To je velmi dobrá aproximace standardní hodnoty gravitace.

Reference

1. Giancoli, D. (2006). Fyzika: Principy s aplikacemi. Šesté vydání. Prentice Hall. 118-122.
2. Hewitt, Paul. (2012). Konceptuální fyzikální věda. Páté vydání. Pearson. 91 - 94.
3. Rex, A. (2011). Základy fyziky. Pearson. 213-221.