The okamžité zrychlení Jedná se o změnu, kterou rychlost zažívá za jednotku času v každém okamžiku pohybu. V přesný okamžik, kdy „dragster„Ze snímku byl vyfotografován a vynesl zrychlení 29,4 m / sdva. To znamená, že v té době byla jeho rychlost zvýšena o 29,4 m / s v rozpětí 1 s. To odpovídá 105 km / h za pouhou 1 sekundu.
Soutěž dragsterů lze snadno modelovat za předpokladu, že závodní auto je bodovým objektem. P který se pohybuje po přímce. Na této přímce je vybrána osa orientovaná počátkem NEBO že budeme nazývat osuVŮL) nebo jen osa X.
Kinematické proměnné, které definují a popisují pohyb, jsou:
Jsou to všechny vektorové veličiny. Proto mají velikost, směr a smysl.
V případě přímočarého pohybu existují pouze dva možné směry: kladný (+) ve směru (VŮL) nebo záporný (-) v opačném směru než (VŮL). Proto je možné upustit od formálního vektorového zápisu a použít znaménka k označení smyslu velikosti.
Rejstřík článků
Předpokládejme, že v tuto chvíli t částice má rychlost v (t) a okamžitě t ' jeho rychlost je v (t ').
Změna, kterou rychlost za tu dobu měla, tedy byla Δv = v (t ') - v (t). Proto zrychlení v časovém úseku Δt = t '- t , by byl dán kvocientem:
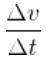
Tento podíl je průměrné zrychlení přim v časovém období Δt mezi okamžiky t a t '.
Pokud bychom chtěli vypočítat zrychlení právě v čase t, pak by t 'mělo být zanedbatelně větší množství než t. S tímto Δt, což je rozdíl mezi těmito dvěma, by měl být téměř nula.
Matematicky je to uvedeno takto: Δt → 0 a získá se:
Já) Částice se pohybuje podél osy X s konstantní rychlostí v0 = 3 m / s. Jaké bude zrychlení částice?
Derivace konstanty je nula, proto je zrychlení částice pohybující se konstantní rychlostí nulové.
II) Po ose se pohybuje částice X a jeho rychlost se mění s časem podle následujícího vzorce:
v (t) = 2 - 3 t
Kde se rychlost měří vm / sa čas v s. Jaké bude zrychlení částice?
)
Výsledek je interpretován takto: pro každý okamžik je zrychlení -3 m / s.
Mezi okamžiky 0 s a 2/3 s je rychlost kladná, zatímco záporné zrychlení, to znamená, že v tomto intervalu částice sníží svou rychlost nebo zpomalí.
V okamžiku 2/3 s se jeho rychlost stane nulovou, ale protože přetrvává zrychlení -3 m / s, od tohoto okamžiku se rychlost obrátí (stane se záporná).
V okamžicích po ⅔ s se částice zrychluje, protože pokaždé, když se její rychlost stává zápornější, to znamená, že její rychlost (modul rychlosti) roste.
III) Obrázek ukazuje křivku, která představuje rychlost jako funkci času pro částici, která se pohybuje podél osy X. Najděte znaménko zrychlení v časech t1, tdva a ty3. Uveďte také, zda se částice zrychluje nebo zpomaluje.
Zrychlení je derivací funkce rychlosti, proto je ekvivalentní sklonu tečny ke křivce v (t) pro daný okamžik t.
Pro okamžité t1, sklon je záporný, takže zrychlení je záporné. A protože v tomto okamžiku je rychlost kladná, můžeme potvrdit, že v tomto okamžiku se částice zpomaluje.
Pro okamžité tdva tečná čára ke křivce v (t) je vodorovná, takže její sklon je nulový. Mobil má nulové zrychlení, tedy při tdva částice ani nezrychluje ani nezpomaluje.
Pro okamžité t3, sklon tečny ke křivce v (t) je kladný. S pozitivním zrychlením se částice skutečně zrychluje, protože v tu chvíli je rychlost také pozitivní.
V předchozí části bylo okamžité zrychlení definováno z okamžité rychlosti. Jinými slovy, pokud je rychlost známa v každém okamžiku, pak je také možné znát zrychlení v každém okamžiku pohybu..
Opačný proces je možný. To znamená, že když známe zrychlení pro každý okamžik, lze vypočítat okamžitou rychlost.
Pokud je operace, která umožňuje přechod z rychlosti na zrychlení, derivací, opačnou matematickou operací je integrace.
Zrychlení částice pohybující se podél osy X je a (t) = ¼ tdva. Kde t se měří v sekundách a vm / s. Určete zrychlení a rychlost částice při 2 s pohybu, s vědomím, že v počátečním okamžiku t0 = 0 byl v klidu.
Za 2 s je zrychlení 1 m / sdva a rychlost pro okamžité t bude dána vztahem:
Objekt se pohybuje podél osy X rychlostí v m / s, danou:
v (t) = 3 tdva - 2 t, kde t se měří v sekundách. Určete zrychlení občas: 0 s, 1 s, 3 s.
Vezmeme-li derivaci v (t) vzhledem k t, získáme zrychlení v kterémkoli okamžiku:
a (t) = 6t -2
Pak a (0) = -2 m / sdva ; a (1) = 4 m / sdva ; a (3) = 16 m / sdva .
Z horní části budovy se uvolní kovová koule. Klesající zrychlení je gravitační zrychlení, které lze aproximovat hodnotou 10 m / s2 a směřovat dolů. Určete rychlost koule 3 s po jejím uvolnění.
Tento problém zahrnuje gravitační zrychlení. Bereme vertikální směr jako pozitivní dolů, máme, že zrychlení koule je:
a (t) = 10 m / sdva
A rychlost bude dána:
Kovová koule je vystřelena nahoru počáteční rychlostí 30 m / s. Zrychlení pohybu je gravitační zrychlení, které lze aproximovat hodnotou 10 m / sdva a ukázal dolů. Určete rychlost koule po 2 s a 4 s po jejím výstřelu.
Svislý směr bude brán jako kladný nahoru. AV takovém případě bude zrychlení pohybu dáno vztahem
a (t) = -10 m / sdva
Rychlost jako funkce času bude dána vztahem:
Po 4 s od vystřelení bude rychlost 30 - 10 ∙ 4 = -10 m / s. Což znamená, že za 4 s koule klesá rychlostí 10 m / s.
Zatím žádné komentáře