
Charakteristiky vlnové amplitudy, vzorce a cvičení

The amplituda vln je maximální posunutí, které bod vlny zažívá s ohledem na rovnovážnou polohu. Vlny se projevují všude a mnoha způsoby ve světě kolem nás: v oceánu, ve zvuku a na struně nástroje, který jej produkuje, ve světle, na zemském povrchu a mnohem více..
Jedním ze způsobů, jak produkovat vlny a studovat jejich chování, je pozorování vibrací struny, která má pevný konec. Při vytváření rušení na druhém konci osciluje každá částice struny a s ní se přenáší energie rušení ve formě posloupnosti pulzů po celé její délce..

Jak se energie šíří, řetězec, který má být dokonale elastický, předpokládá typický sinusový tvar s hřebeny a údolími, které jsou znázorněny na obrázku níže v další části..
Rejstřík článků
- 1 Charakteristiky a význam amplitudy vln
- 2 Matematický popis vlny
- 3 Popis vlny v čase: charakteristické parametry
- 4 Cvičení vyřešeno
- 4.1 Odpovědi
Charakteristika a význam vlnové amplitudy
Amplituda A je vzdálenost mezi hřebenem a referenční osou nebo úrovní 0. Pokud je to výhodné, mezi údolím a referenční osou. Pokud je rušení ve struně mírné, je amplituda A malá. Pokud je naopak narušení intenzivní, bude amplituda větší.
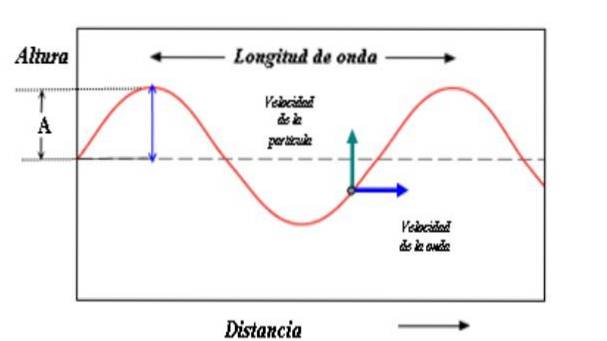
Hodnota amplitudy je také měřítkem energie přenášené vlnou. Je intuitivní, že velká amplituda je spojena s vyššími energiemi.
Ve skutečnosti je energie úměrná druhé mocnině amplitudy, která, vyjádřená matematicky, je:
Já ∝Adva
Kde I je intenzita vlny, která se zase vztahuje k energii.
Typ vlny produkované v řetězci v příkladu patří do kategorie mechanických vln. Důležitou charakteristikou je, že každá částice v řetězci je vždy udržována velmi blízko své rovnovážné polohy..
Částice se nepohybují ani neprocházejí řetězcem. Houpají se nahoru a dolů. To je ve výše uvedeném diagramu indikováno zelenou šipkou, avšak vlna spolu se svou energií putuje zleva doprava (modrá šipka).
Vlny, které se šíří ve vodě, poskytují nezbytné důkazy, abyste se o tom přesvědčili. Při pozorování pohybu listu, který spadl do rybníka, je zřejmé, že jednoduše osciluje doprovázející pohyb vody. Nejde to příliš daleko, pokud samozřejmě neexistují jiné síly, které jí zajišťují další pohyby.
Vlnový vzor zobrazený na obrázku sestává z opakujícího se vzoru, ve kterém je vzdálenost mezi dvěma hřebeny vlnová délka λ. Pokud chcete, vlnová délka také odděluje dva stejné body na vlně, i když nejsou na vrcholu..
Matematický popis vlny
Vlnu lze přirozeně popsat matematickou funkcí. Periodické funkce, jako je sinus a kosinus, jsou ideální pro daný úkol, ať už chcete reprezentovat vlnu v prostoru i čase..
Pokud nazýváme svislou osu na obrázku „y“ a vodorovnou osu nazýváme „t“, pak je chování vlny v čase vyjádřeno:
y = A cos (ωt + δ)
Pro tento ideální pohyb osciluje každá částice struny jednoduchým harmonickým pohybem, který vzniká díky síle, která je přímo úměrná posunutí částice..
V navrhované rovnici jsou A, ω a δ parametry, které popisují pohyb, přičemž A je amplituda dříve definováno jako maximální posun, který částice dosáhl vzhledem k referenční ose.
Argument kosinu se nazývá pohybová fáze a δ je fázová konstanta, což je fáze, když t = 0. Kosinová funkce i sinusová funkce jsou vhodné k popisu vlny, protože se od sebe liší pouze π / 2.
Obecně je možné pro zjednodušení výrazu zvolit t = 0 s δ = 0 a získat:
y = A cos (ωt)
Protože se pohyb opakuje jak v prostoru, tak v čase, existuje charakteristický čas, kterým je období T, je definován jako čas potřebný k tomu, aby částice provedla úplnou oscilaci.
Popis vlny v čase: charakteristické parametry
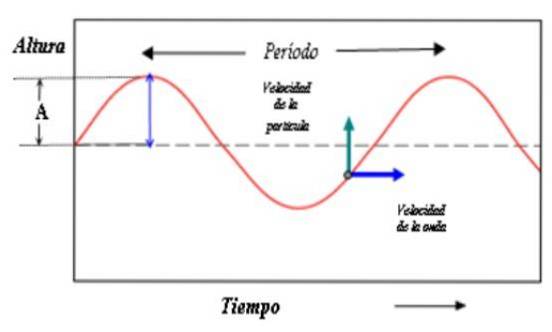
Nyní sinus i kosinus opakují svoji hodnotu, když se fáze zvýší o hodnotu 2π, takže:
ωT = 2π → ω = 2π / T
Ω se volá úhlová frekvence pohybu y má rozměry inverzní funkce času, přičemž je jeho jednotkami v mezinárodním systému radián / sekunda nebo sekunda-1.
Nakonec můžete definovat frekvence pohybu f, jako inverzní nebo reciproční období. Představuje počet vrcholů za jednotku času, v takovém případě:
f = 1 / T.
ω = 2πf
F i ω mají stejné rozměry a jednotky. Kromě toho druhého-1, který se nazývá Hertz nebo Hertz, je běžné slyšet otáčky za sekundu nebo otáčky za minutu.
Rychlost vlny proti, což je nutné zdůraznit, že to není totéž jako u částic, lze jej snadno vypočítat, jsou-li známy vlnové délky λ a frekvence f:
v = λf
Pokud je kmitání částic jednoduché harmonické, úhlová frekvence a frekvence závisí pouze na povaze kmitajících částic a vlastnostech systému. Amplituda vlny tyto parametry neovlivňuje.
Například při hraní na notu na kytaru bude mít nota vždy stejný tón, i když se hraje s větší nebo menší intenzitou, tímto způsobem bude C vždy znít jako C, i když je slyšet hlasitěji nebo měkčí ve skladbě, ať už na klavír nebo na kytaru.
V přírodě jsou vlny, které jsou transportovány v hmotném médiu ve všech směrech, oslabeny, protože energie je rozptýlena. Z tohoto důvodu klesá amplituda s inverzní vzdáleností r ke zdroji, přičemž je možné potvrdit, že:
A∝1 / r
Cvičení vyřešeno
Obrázek ukazuje funkci y (t) pro dvě vlny, kde Y je v metrech a t během několika sekund. Pro každý nález:
a) Amplituda
b) Období
c) Frekvence
d) Rovnice každé vlny z hlediska sinusů nebo kosinů.
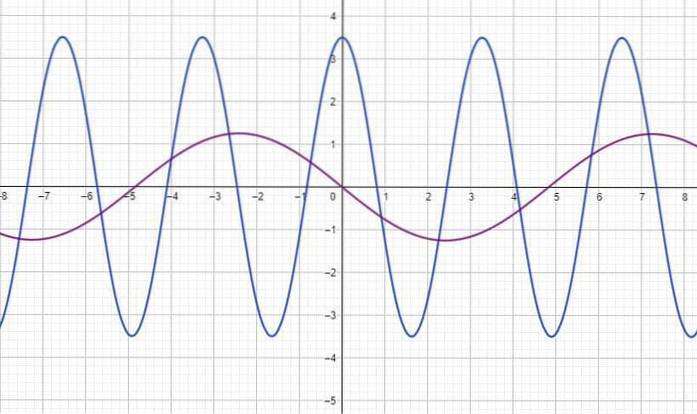
Odpovědi
a) Měří se přímo z grafu pomocí mřížky: modrá vlna: A = 3,5 m; fuchsiová vlna: A = 1,25 m
b) Načte se také z grafu a určuje se vzdálenost mezi dvěma po sobě následujícími vrcholy nebo údolími: modrá vlna: T = 3,3 sekundy; fuchsiová vlna T = 9,7 sekundy
c) Vypočítává se s pamětí, že frekvence je převrácená hodnota periody: modrá vlna: f = 0,302 Hz; fuchsiová vlna: f = 0,103 Hz.
d) Modrá vlna: y (t) = 3,5 cos (ωt) = 3,5 cos (2πf.t) = 3,5 cos (1,9 t) m; Fuchsiová vlna: y (t) = 1,25 sin (0,65t) = 1,25 cos (0,65t + 1,57)
Všimněte si, že fuchsiová vlna je mimo fázi π / 2 vzhledem k modré, je možné ji reprezentovat pomocí sinusové funkce. Nebo kosinus posunul π / 2.



Zatím žádné komentáře