
Typy pravděpodobnostních axiomů, vysvětlení, příklady, cvičení
The axiomy pravděpodobnost jsou to matematické návrhy odkazující na teorii pravděpodobnosti, které si nezaslouží důkaz. Axiomy založil v roce 1933 ruský matematik Andrej Kolmogorov (1903-1987) ve své práci Základy teorie pravděpodobnosti a položil základy pro matematické studium pravděpodobnosti.
Při provádění určitého náhodného experimentu ξ je ukázkový prostor E souborem všech možných výsledků experimentu, také nazývaných Události. Jakákoli událost je označena jako A a P (A) je pravděpodobnost jejího výskytu. Poté Kolmogorov zjistil, že:

-Axiom 1 (ne negativita): pravděpodobnost výskytu jakékoli události A je vždy kladná nebo nulová, P (A) ≥0. Když je pravděpodobnost události 0, je volána nemožná událost.
-Axiom 2 (jistota): kdykoli nějaká událost patřící k E, její pravděpodobnost výskytu je 1, což můžeme vyjádřit jako P (E) = 1. To je to, co je známé jako jistá událost, protože při provádění experimentu je se vší jistotou výsledek.
-Axiom 3 (doplněk): v případě dvou nebo více nekompatibilních událostí po dvou, nazývaných A1, NAdva, NA3…, Pravděpodobnost, že dojde k události A.1 plus Adva plus A3 a tak dále, je to součet pravděpodobností, že se každá stane zvlášť.
To je vyjádřeno jako: P (A.1 U Adva U A3 U…) = P (A1) + P (A.dva) + P (A.3) + ...

Rejstřík článků
- 1 Příklad
- 2 způsoby, jak přiřadit pravděpodobnost
- 2.1 Laplaceovo pravidlo
- 2.2 Relativní frekvence
- 3 Cvičení vyřešeno
- 3.1 Řešení a
- 4 Odkazy
Příklad
Axiomy pravděpodobnosti jsou široce používány v mnoha aplikacích. Například:
Připínáček nebo připínáček je vyhozen do vzduchu, a když spadne na podlahu, je zde možnost přistání s hrotem nahoru (U) nebo s hrotem dolů (D) (nebudeme uvažovat o dalších možnostech). Ukázkový prostor tohoto experimentu se skládá z těchto událostí, pak E = U, D.

Použitím axiomů máme:
P (E) = 1 (Axiom 2)
Ale P (E) = P (U) + P (D) (Axiom 3), protože tyto události jsou vzájemně nekompatibilní nebo nesouvislé. Připínáček neklesá špičkou současně nahoru nebo dolů, je to jeden nebo druhý, ale ne obojí, protože nejsou brány v úvahu jiné možnosti. Pak:
P (U) + P (D) = 1
P (U) = 1 - P (D)
Ať už je stejně pravděpodobné, že přistanete nahoru nebo dolů, P (U) = P (D) = ½ (Axiom 1). Může se však stát, že konstrukce a design připínáčku pravděpodobně spadne tak či onak. Může to být například tak P (U) = ¾ zatímco P (D) = ¼ (Axiom 1).
Všimněte si, že v obou případech součet pravděpodobností dává 1. Axiomy však neindikují, jak přiřadit pravděpodobnosti, alespoň ne úplně. Potvrzují však, že se jedná o čísla mezi 0 a 1, a že jako v tomto případě je součet všech 1.
Způsoby přiřazení pravděpodobnosti
Axiomy pravděpodobnosti nejsou metodou přiřazování hodnoty pravděpodobnosti. K tomu existují tři možnosti, které jsou kompatibilní s axiomy:
Laplaceovo pravidlo
Každá událost má přiřazenu stejnou pravděpodobnost, že se stane, pak je pravděpodobnost výskytu definována jako:
P (A) = počet případů příznivých pro událost A / počet možných případů
Jaká je například pravděpodobnost tažení esa z balíčku francouzských karet? Balíček má 52 karet, z každé barvy 13 a jsou zde 4 barvy. Každá barva má 1 esa, takže celkem existují 4 esa:
P (jako) = 4/52 = 1/13
Laplaceovo pravidlo je omezeno na konečné vzorové prostory, kde je každá událost stejně pravděpodobná.
Relativní frekvence
Zde musí být experiment opakovatelný, protože metoda je založena na provádění velkého počtu opakování..
Udělejme i opakování experimentu ξ, z nichž zjistíme, že n je počet výskytů určité události A, pravděpodobnost, že k této události dojde, je:
P (A) = limi → ∞ (ani)
Kde n / i je relativní frekvence události.
Definování P (A) tímto způsobem uspokojuje Kolmogorovovy axiomy, ale má tu nevýhodu, že je třeba provést mnoho testů, aby byla pravděpodobnost vhodná.
Subjektivní metoda
Osoba nebo skupina lidí může souhlasit s přiřazením pravděpodobnosti události na základě vlastního úsudku. Tato metoda má tu nevýhodu, že různí lidé mohou stejné události přiřadit různé pravděpodobnosti..
Cvičení vyřešeno
V experimentu současného házení 3 poctivých mincí získejte pravděpodobnosti popsaných událostí:
a) 2 hlavy a ocas.
b) 1 hlava a dva ocasy
c) 3 kříže.
d) Nejméně 1 obličej.
Řešení
Hlavy jsou označeny C a ocasy X. Existuje ale několik způsobů, jak získat dvě hlavy a ocas. Například první dvě mince mohou přistát hlavy a třetí mohou přistát ocasy. Nebo první může spadnout hlavy, druhý ocasy a třetí hlavy. A konečně první mohou být ocasy a zbývající hlavy.
Pro zodpovězení otázek je nutné znát všechny možnosti, které jsou popsány v nástroji zvaném stromový diagram nebo strom pravděpodobností:
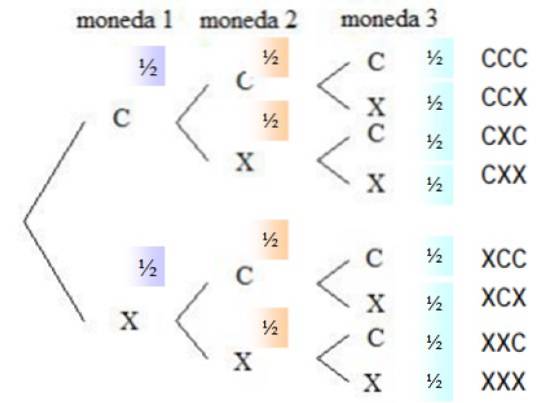
Pravděpodobnost, že nějaká mince vyjde z hlavy, je ½, totéž platí pro ocasy, protože mince je upřímná. V pravém sloupci jsou uvedeny všechny možnosti, které má los, tj. Ukázkový prostor.
Z ukázkového prostoru jsou vybrány kombinace, které reagují na požadovanou událost, protože pořadí, ve kterém se tváře objevují, není důležité. Existují tři příznivé události: CCX, CXC a XCC. Pravděpodobnost výskytu každé události je:
P (CCX) = ½. ½. ½ = 1/8
Totéž se děje u událostí CXC a XCC, každá z nich má 1/8 pravděpodobnost výskytu. Pravděpodobnost získání přesně 2 hlav je tedy součtem pravděpodobností všech příznivých událostí:
P (2stranný) = 1/8 + 1/8 + 1/8 = 3/8 = 0,375
Řešení b
Nalezení pravděpodobnosti, že nastanou přesně dva křížení, je problém analogický s předchozím, existují také tři příznivé události převzaté z ukázkového prostoru: CXX, XCX a XXC. Proto:
P (2 kříže) = 3/8 = 0,375
Řešení c
Intuitivně víme, že pravděpodobnost získání 3 ocasů (nebo 3 hlav) je nižší. V tomto případě je hledaná událost XXX na konci pravého sloupce, jehož pravděpodobnost je:
P (XXX) = ½. ½. ½ = 1/8 = 0,125.
Řešení d
Je požadováno získat alespoň 1 obličej, to znamená, že mohou vyjít 3 obličeje, 2 obličeje nebo 1 obličej. Jedinou s tím neslučitelnou událostí je událost, ve které vyjdou 3 ocasy, jejichž pravděpodobnost je 0,125. Hledaná pravděpodobnost je tedy:
P (alespoň 1 hlava) = 1 - 0,125 = 0,875.
Reference
- Canavos, G. 1988. Pravděpodobnost a statistika: Aplikace a metody. Mcgraw kopec.
- Devore, J. 2012. Pravděpodobnost a statistika pro inženýrství a vědu. 8. Edice. Cengage.
- Lipschutz, S. 1991. Schaum Series: Probability. Mcgraw kopec.
- Obregón, I. 1989. Teorie pravděpodobnosti. Redakční Limusa.
- Walpole, R. 2007. Pravděpodobnost a statistika pro strojírenství a vědy. Pearson.



Zatím žádné komentáře