The jednotková buňka Je to imaginární prostor nebo oblast, která představuje minimální vyjádření celku; že v případě chemie by celek byl krystal složený z atomů, iontů nebo molekul, které jsou uspořádány podle strukturního vzoru.
V každodenním životě lze najít příklady, které tento koncept ztělesňují. Za tímto účelem je nutné věnovat pozornost objektům nebo povrchům, které vykazují určité opakující se pořadí jejich prvků. Některé mozaiky, reliéfy, kazetové stropy, plechy a tapety mohou obecně zahrnovat to, čemu rozumí jednotková buňka.
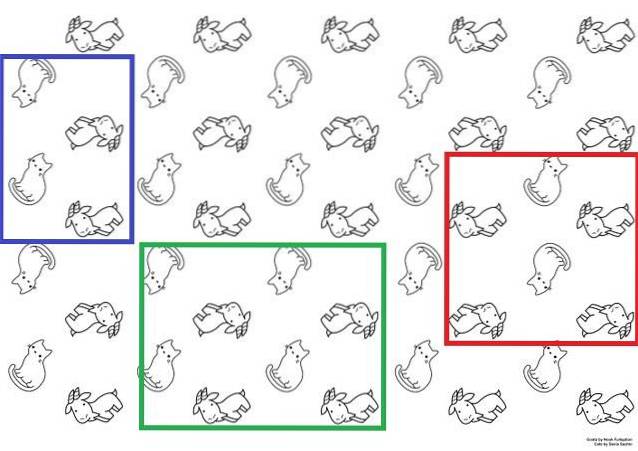
Pro jasnější ilustraci je zde obrázek nahoře, který lze použít jako tapetu. V něm se kočky a kozy objevují se dvěma alternativními smysly; kočky jsou vzpřímené nebo vzhůru nohama a kozy leží vleže obrácené nahoru nebo dolů.
Tyto kočky a kozy vytvářejí opakující se strukturní sekvenci. K sestavení celého papíru by stačilo reprodukovat jednotkovou buňku po povrchu dostatečně mnohokrát pomocí translačních pohybů..
Možné jednotkové buňky jsou reprezentovány modrým, zeleným a červeným rámečkem. K získání role bylo možné použít kteroukoli z těchto tří; ale je nutné je imaginativně pohybovat po povrchu, aby se zjistilo, zda reprodukují stejnou sekvenci pozorovanou na obrázku.
Počínaje červeným rámečkem by bylo oceněno, že pokud by byly tři sloupce (kočky a kozy) přesunuty doleva, dole by se již neobjevily dvě kozy, ale pouze jedna. Proto by to vedlo k další sekvenci a nelze ji považovat za jednotkovou buňku.
Zatímco kdyby pomyslně posunuli dvě pole, modrou a zelenou, získala by se stejná posloupnost papíru. Oba jsou jednotkové buňky; modrý rámeček se však více řídí definicí, protože je menší než zelený rámeček.
Rejstřík článků
Jeho vlastní definice, kromě právě vysvětleného příkladu, objasňuje několik jeho vlastností:
-Pokud se budete pohybovat v prostoru, bez ohledu na směr, získáte kompletní těleso nebo krystal. Je to proto, že, jak již bylo zmíněno u koček a koz, reprodukují strukturní sekvenci; což se rovná prostorovému rozložení opakujících se jednotek.
-Musí být co nejmenší (nebo zabírají malý objem) ve srovnání s jinými možnými možnostmi buněk.
-Obvykle jsou symetrické. Jeho symetrie se také doslova odráží v krystalech sloučeniny; pokud je jednotková buňka soli kubická, její krystaly budou krychlové. Existují však krystalické struktury, které jsou popsány s jednotkovými buňkami se zkreslenou geometrií..
-Obsahují opakující se jednotky, které mohou být nahrazeny body, které zase tvoří to, co je známé jako mřížka ve třech rozměrech. V předchozím příkladu představují kočky a kozy mřížové body při pohledu z vyšší roviny; tj. dvě dimenze.
Opakující se jednotky nebo mřížkové body jednotkových buněk udržují stejný podíl pevných částic.
Pokud spočítáte počet koček a koz v modrém poli, budete mít dvě kočky a kozy. Totéž se děje se zeleným rámečkem a také s červeným rámečkem (i když je již známo, že nejde o jednotkovou buňku).
Předpokládejme například, že kočky a kozy jsou atomy G a C (podivné zvířecí svary). Protože poměr G k C je 2: 2 nebo 1: 1 v modrém poli, lze bezpečně očekávat, že těleso bude mít vzorec GC (nebo CG).
Když pevná látka vykazuje více či méně kompaktní struktury, jako je tomu u solí, kovů, oxidů, sulfidů a slitin, v jednotkových buňkách nejsou celé opakující se jednotky; to znamená, že existují jejich části nebo části, které tvoří až jednu nebo dvě jednotky.
To není případ GC. Pokud ano, modrý rámeček by „rozdělil“ kočky a kozy na dvě (1 / 2G a 1 / 2C) nebo čtyři (1 / 4G a 1 / 4C). V dalších částech bude vidět, že v těchto jednotkových buňkách jsou retikulární body pohodlně rozděleny tímto a dalšími způsoby..
Jednotkové buňky v příkladu GC jsou dvourozměrné; to však neplatí pro skutečné modely, které berou v úvahu všechny tři dimenze. Čtverce nebo rovnoběžníky se tedy transformují na rovnoběžnostěny. Nyní má výraz „buňka“ větší smysl.
Rozměry těchto buněk nebo rovnoběžnostěn závisí na délce jejich příslušných stran a úhlů..
Na dolním obrázku máte spodní zadní roh rovnoběžnostěnu složený ze stran na, b Y C, a úhly α, β a γ.
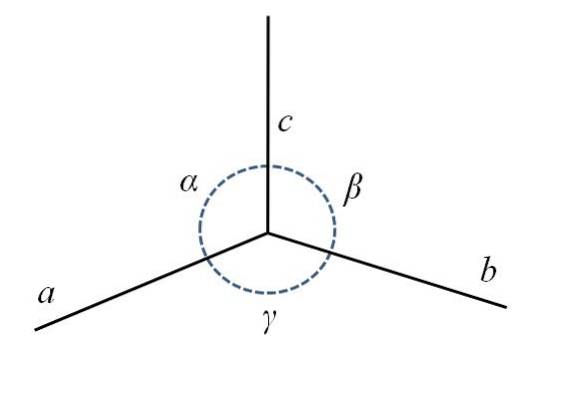
Jak můžete vidět, na je o něco delší než b Y C. Ve středu je tečkovaný kruh, který označuje úhly α, β a γ mezi nimi ac, cb Y ba, resp. Pro každou jednotkovou buňku mají tyto parametry konstantní hodnoty a definují její symetrii a symetrii zbytku krystalu..
Opětovné použití určité představivosti by parametry obrazu definovaly buňku podobnou kostce roztaženou na jejím okraji. na. Jednotkové buňky tedy vznikají s různými délkami a úhly jejich hran, které lze také rozdělit do různých typů.
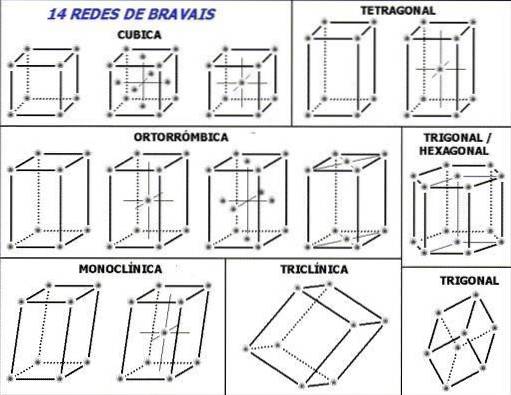
Poznámka: začněte v horním obrázku tečkovanými čarami v jednotkových buňkách: označují spodní zadní úhel, jak bylo právě vysvětleno. Lze si položit následující otázku, kde jsou mřížové body nebo opakující se jednotky? I když dávají nesprávný dojem, že buňky jsou prázdné, odpověď leží na jejich vrcholech.
Tyto buňky jsou generovány nebo vybírány takovým způsobem, že opakující se jednotky (šedavé body obrázku) jsou umístěny na jejich vrcholech. V závislosti na hodnotách parametrů stanovených v předchozí části, konstantní pro každou jednotkovou buňku, je odvozeno sedm krystalových systémů.
Každý krystalový systém má svou vlastní jednotkovou buňku; druhý definuje první. V horním obrázku je sedm čtverců, odpovídajících sedmi krystalickým systémům; nebo trochu souhrnněji řečeno krystalické sítě. Například kubická jednotková buňka odpovídá jednomu z krystalových systémů, který definuje krychlovou krystalovou mřížku.
Podle obrázku jsou krystalické systémy nebo sítě:
-Krychlový
-Tetragonální
-Ortorombický
-Šestihranný
-Monoklinický
-Triclinic
-Trigonální
A v těchto krystalických systémech vznikají další, které tvoří čtrnáct Bravaisových sítí; že ze všech krystalických sítí jsou nejzákladnější.
V krychli jsou všechny její strany a úhly stejné. Proto v této jednotkové buňce platí následující:
na = b = C
α = β = γ = 90 °
Existují tři kubické jednotkové buňky: jednoduché nebo primitivní, centrované na tělo (bcc) a na obličej (fcc). Rozdíly spočívají v tom, jak jsou body rozloženy (atomy, ionty nebo molekuly) a v jejich počtu.
Která z těchto buněk je nejkompaktnější? Ten, jehož objem je více obsazen body: kubický se středem na tvářích. Všimněte si, že kdybychom tečky a kozy od začátku nahradili tečkami, neomezily by se na jedinou buňku; patřili by a sdílelo by je několik. Opět by to byly části G nebo C..
Pokud by kočky nebo kozy byly na vrcholcích, sdílelo by je 8 jednotkových buněk; to znamená, že každá buňka bude mít 1/8 G nebo C. Spojte se nebo si představte 8 kostek ve dvou sloupcích po dvou řádcích, aby se to zobrazilo.
Pokud by na tvářích byly kočky nebo kozy, sdílely by je pouze 2 jednotkové buňky. Chcete-li to vidět, stačí dát dvě kostky dohromady.
Na druhou stranu, pokud by byla kočka nebo koza ve středu krychle, patřily by pouze do jediné jednotkové buňky; Totéž se děje s rámečky na hlavním obrázku, když byl koncept řešen.
Řeklo to výše, uvnitř jednoduché kubické jednotkové buňky, kterou máme A jednotka nebo mřížový bod, protože má 8 vrcholů (1/8 x 8 = 1). Pro kubickou buňku se středem v těle existuje: 8 vrcholů, což se rovná atomu, a bod nebo jednotka ve středu; proto existuje dva Jednotky.
A pro kubickou buňku se středem tváře existuje: 8 vrcholů (1) a šest ploch, kde je sdílena polovina každého bodu nebo jednotky (1/2 x 6 = 3); proto má čtyři Jednotky.
Podobné poznámky lze učinit ohledně jednotkové buňky pro tetragonální systém. Jeho strukturální parametry jsou následující:
na = b ≠ C
α = β = γ = 90 °
Parametry pro ortorombickou buňku jsou:
na ≠ b ≠ C
α = β = γ = 90 °
Parametry pro monoklinickou buňku jsou:
na ≠ b ≠ C
a = γ = 90 °; β ≠ 90 °
Parametry triclinické buňky jsou:
na ≠ b ≠ C
α ≠ β ≠ γ ≠ 90 °
Parametry pro hexagonální buňku jsou:
na = b ≠ C
a = p = 90 °; γ ≠ 120 °
Buňka ve skutečnosti tvoří jednu třetinu šestihranného hranolu.
A konečně, parametry pro trigonální buňku jsou:
na = b = C
α = β = γ ≠ 90 °
Zatím žádné komentáře