
Fáze Carnotova cyklu, aplikace, příklady, cvičení
The Carnotův cyklus je to sled termodynamických procesů, které probíhají v Carnotově motoru, ideálním zařízení, které se skládá pouze z procesů reverzibilního typu; tj. ty, které se uskutečnily, se mohou vrátit do původního stavu.
Tento typ motoru je považován za ideální, protože postrádá rozptyl, tření nebo viskozitu, které vznikají ve skutečných strojích a které přeměňují tepelnou energii na použitelnou práci, i když se převod neprovádí 100%.

Motor se vyrábí z látky schopné vykonávat práci, jako je benzín, benzín nebo pára. Tato látka je vystavena různým změnám teploty a následně dochází ke změnám jejího tlaku a objemu. Tímto způsobem je možné pohybovat pístem uvnitř válce.
Rejstřík článků
- 1 Co je Carnotův cyklus?
- 2 fáze Carnotova cyklu
- 2.1 Výchozí bod
- 2.2 První fáze: izotermická expanze
- 2.3 Druhá fáze: adiabatická expanze
- 2.4 Třetí fáze: izotermická komprese
- 2.5 Čtvrtá fáze: adiabatická komprese
- 3 Carnotova věta
- 3.1 Důkaz Carnotovy věty
- 3.2 Důsledek věty a omezení
- 4 příklady
- 4.1 Píst uvnitř válce
- 4.2 Různé reverzibilní procesy
- 4.3 Jaderná elektrárna
- 5 Cvičení vyřešena
- 5.1 - Příklad 1: účinnost tepelného motoru
- 5.2 - Příklad 2: absorbované teplo a přenesené teplo
- 6 Reference
Co je Carnotův cyklus?
Carnotův cyklus probíhá v systému zvaném Carnotův motor nebo C, což je ideální plyn uzavřený ve válci a opatřený pístem, který je v kontaktu se dvěma zdroji při různých teplotách T1 a Tdva jako na obrázku vlevo.
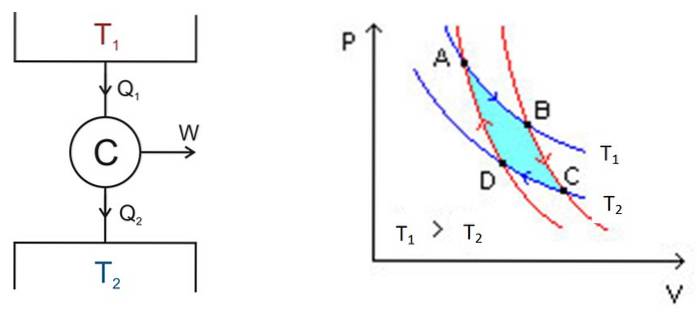
Tam probíhají následující hrubé procesy:
- Zařízení Q se dodává určité množství teplavstup = Q1 z tepelné nádrže při vysoké teplotě T1.
- Carnotův motor C díky tomuto dodanému teplu vykonává práci W.
- Část použitého tepla: odpad Qvýstup, se převádí do tepelné nádrže, která má nižší teplotu T.dva.
Fáze Carnotova cyklu
Analýza se provádí pomocí diagramu P-V (tlak-objem), jak je znázorněno na obrázku 2 (pravý obrázek). Účelem motoru může být udržování chladicího tepelného zásobníku 2 a získávání tepla z něj. V tomto případě se jedná o chladicí stroj. Pokud naopak chcete přenášet teplo do tepelné nádrže 1, pak je to a tepelné čerpadlo.
Diagram P-V ukazuje změny tlaku - teploty motoru za dvou podmínek:
- Udržování konstantní teploty (izotermický proces).
- Žádný přenos tepla (tepelná izolace).
Je třeba spojit dva izotermické procesy, čehož je dosaženo tepelnou izolací.
Směřovat
Můžete začít v kterémkoli bodě cyklu, ve kterém má plyn určité podmínky tlaku, objemu a teploty. Plyn prochází řadou procesů a může se vrátit do výchozích podmínek, aby zahájil další cyklus, a konečná vnitřní energie je vždy stejná jako počáteční. Protože energie je zachována:
Práce provedená C = tepelný příkon - tepelný výkon
ΔW = Qvstup - Qvýstup
Plocha v této smyčce nebo smyčce, na obrázku tyrkysová, je přesně ekvivalentní práci provedené motorem Carnot.
Na obrázku 2 jsou označeny body A, B, C a D. Začneme v bodě A podle modré šipky..
První fáze: izotermická expanze
Teplota mezi body A a B je T1. Systém absorbuje teplo z tepelného zásobníku 1 a prochází izotermickou expanzí. Pak se objem zvýší a tlak se sníží.
Teplota však zůstává na T1, protože když plyn expanduje, ochlazuje se. Proto jeho vnitřní energie zůstává konstantní.
Druhá fáze: adiabatická expanze
V bodě B systém zahájí novou expanzi, ve které systém nezískává ani neztrácí teplo. Toho je dosaženo umístěním do tepelné izolace, jak je uvedeno výše. Jedná se tedy o adiabatickou expanzi, která pokračuje do bodu C podle červené šipky. Zvyšuje se objem a tlak klesá na nejnižší hodnotu.
Třetí fáze: izotermická komprese
Začíná to v bodě C a končí v D. Izolace se odstraní a systém přijde do kontaktu s tepelnou nádrží 2, jejíž teplota Tdva je méně. Systém přenáší odpadní teplo do tepelného zásobníku, tlak se začíná zvyšovat a objem se zmenšuje.
Čtvrtá fáze: adiabatická komprese
V bodě D se systém vrátí k tepelné izolaci, tlak se zvyšuje a objem klesá, dokud nedosáhne původních podmínek bodu A. Potom se cyklus znovu opakuje..
Carnotova věta
Carnotova věta byla poprvé postulována na počátku 19. století francouzským fyzikem Sadi Carnotem. V roce 1824 Carnot, který byl součástí francouzské armády, vydal knihu, ve které navrhl odpověď na následující otázku: za jakých podmínek má tepelný motor maximální účinnost? Carnot poté stanovil následující:
Žádný tepelný motor běžící mezi dvěma tepelnými zásobníky není účinnější než motor Carnot.
Účinnost η tepelného motoru je dána kvocientem mezi provedenou prací W a absorbovaným teplem Q:
výkon = odvedená práce / absorbované teplo
Tímto způsobem je účinnost jakéhokoli tepelného motoru I: η = W / Q. Zatímco účinnost Carnotova motoru R je η '= W / Q', za předpokladu, že oba motory jsou schopné vykonávat stejnou práci.
Carnotova věta říká, že η nikdy není větší než η '. Jinak je to v rozporu s druhým zákonem termodynamiky, podle kterého je nemožný proces, jehož výsledkem je, že teplo vychází z tělesa s nižší teplotou a jde na vyšší teplotu bez přijímání vnější pomoci. Proto:
η < η''
Důkaz Carnotovy věty
Chcete-li ukázat, že tomu tak je, zvažte motor Carnot fungující jako chladicí stroj poháněný motorem I. To je možné, protože motor Carnot pracuje reverzibilními procesy, jak je uvedeno na začátku..
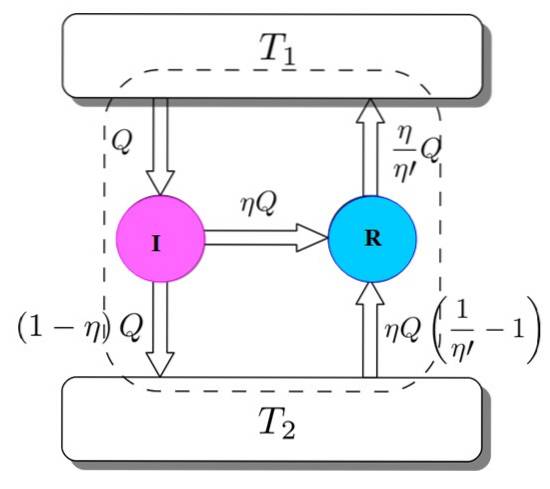
Oba máme: I i R pracují se stejnými tepelnými nádržemi a bude se předpokládat, že η > η''. Pokud je na cestě rozpor s druhým zákonem termodynamiky, Carnotova věta je prokázána redukcí na absurditu.
Obrázek 3 vám pomůže tento proces sledovat. Motor I přijímá množství tepla Q, které rozděluje tímto způsobem: práce na R ekvivalentní W = ηQ a zbytek je teplo přenášené (1-η) Q do tepelného zásobníku Tdva.
Jelikož je energie zachována, jsou splněny všechny následující podmínky:
Avstup = Q = Práce W + teplo dané Tdva = ηQ + (1-η) Q = Evýstup
Nyní Carnotův chladicí stroj R odebírá z tepelného zásobníku 2 množství tepla dané:
(η / η ') (1-η') Q =
Energie musí být také zachována v tomto případě:
Avstup = ηQ + (η / η ') (1-η') Q = (η / η ') Q = Q' = Evýstup
Výsledkem je přenos do tepelné nádrže Tdva množství tepla dané (η / η ') Q = Q'.
Pokud je η větší než η ', znamená to, že více tepla dosáhlo tepelného nánosu vyšší teploty, než jsem původně vzal. Vzhledem k tomu, že se neúčastnil žádný externí činitel, například jiný zdroj tepla, může dojít pouze k tomu, aby se nejchladnější tepelná nádrž vzdala tepla..
To je v rozporu s druhým zákonem termodynamiky. Vyvozuje se tedy závěr, že není možné, že η'' je menší než η, proto motor I nemůže mít větší účinnost než Carnotův stroj R.
Důsledek věty a omezení
Důsledek Carnotovy věty uvádí, že dva Carnotovy stroje mají stejnou účinnost, pokud pracují se stejnými tepelnými zásobníky..
To znamená, že bez ohledu na látku je výkon nezávislý a nelze jej zvýšit jeho změnou..
Závěr z výše uvedené analýzy je, že Carnotův cyklus je ideálně dosažitelnou špičkou termodynamického procesu. V praxi existuje mnoho faktorů, které snižují účinnost, například skutečnost, že izolace není nikdy dokonalá a v adiabatických fázích skutečně dochází k výměně tepla s vnějším.
V případě automobilu se blok motoru zahřívá. Na druhou stranu se směs benzínu a vzduchu nechová přesně jako ideální plyn, což je výchozí bod Carnotova cyklu. To zmiňuje jen několik faktorů, které způsobí drastické snížení výkonu.
Příklady
Píst uvnitř válce
Pokud je systémem píst uzavřený ve válci, jak je znázorněno na obrázku 4, píst stoupá během izotermické expanze, jak je vidět na prvním schématu zcela vlevo, a také stoupá během adiabatické expanze.
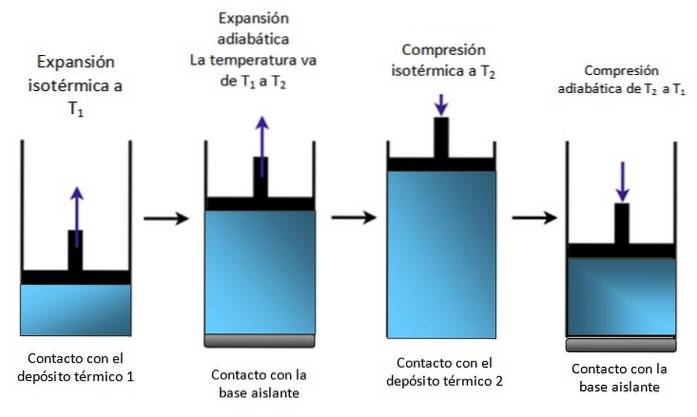
Poté se izotermicky komprimuje, vzdává se tepla a pokračuje v adiabatickém stlačení. Výsledkem je pohyb, při kterém píst prochází nahoru a dolů uvnitř válce a který lze přenášet na další části konkrétního zařízení, například na motor automobilu, který produkuje točivý moment, nebo na parní stroj.
Různé reverzibilní procesy
Kromě expanze a komprese ideálního plynu uvnitř lahve existují další ideální reverzibilní procesy, pomocí kterých lze konfigurovat Carnotův cyklus, například:
- Pohyby tam a zpět bez tření.
- Ideální pružina, která stlačuje a dekomprimuje a nikdy se nedeformuje.
- Elektrické obvody, ve kterých nejsou žádné odpory k rozptýlení energie.
- Magnetizační a demagnetizační cykly, ve kterých nedochází ke ztrátám.
- Nabíjení a vybíjení baterie.
Jaderná elektrárna
Ačkoli se jedná o velmi složitý systém, první přiblížení toho, co je zapotřebí k výrobě energie v jaderném reaktoru, je následující:
- Tepelný zdroj, sestávající z radioaktivně se rozpadajícího materiálu, jako je uran.
- Chladný chladič nebo zásobník, kterým by byla atmosféra.
- „Carnotův motor“, který využívá kapalinu téměř vždy z vodovodu, do které se dodává teplo z tepelného zdroje, aby se přeměnilo na páru.
Když je cyklus prováděn, je elektrická energie získávána jako čistá práce. Při přeměně na páru při vysoké teplotě se voda dostane k turbíně, kde se energie přemění na pohybovou nebo kinetickou energii.
Turbína zase pohání elektrický generátor, který transformuje energii svého pohybu na elektrickou energii. Kromě štěpného materiálu, jako je uran, lze samozřejmě jako zdroj tepla použít i fosilní paliva..
Vyřešená cvičení
-Příklad 1: účinnost tepelného motoru
Účinnost tepelného motoru je definována jako podíl mezi prací na vstupu a prací na vstupu, a proto se jedná o bezrozměrnou veličinu:
Maximální účinnost = (Qvstup - Q výstup) / Qvstup
Označíme maximální účinnost jako emax, je možné prokázat jeho závislost na teplotě, což je nejjednodušší měřitelná proměnná, například:
amax = 1 - (T.dva/ T1)
Kde Tdva je teplota jímky a T1 je teplota zdroje tepla. Protože druhá je větší, účinnost se vždy ukáže být menší než 1.
Předpokládejme, že máte tepelný motor schopný pracovat následujícími způsoby: a) mezi 200 K a 400 K, b) mezi 600 K a 400 K. Jaká je účinnost v každém případě?
Řešení
a) V prvním případě je účinnost:
amax1 = 1 - (200/400) = 0,50
b) Pro druhý režim bude účinnost:
amax2 = 1- (400/600) = 0,33
I když je teplotní rozdíl mezi oběma režimy stejný, účinnost není. A ještě pozoruhodnější je, že nejúčinnější režim pracuje při nižší teplotě..
-Příklad 2: absorbované teplo a uvolněné teplo
22% efektivní tepelný motor produkuje 1530 J práce. Najděte: a) množství tepla absorbovaného z tepelné nádrže 1, b) množství tepla odváděného do tepelné nádrže 2.
a) V tomto případě se použije definice účinnosti, protože jsou k dispozici provedené práce, nikoli teploty tepelných nádrží. 22% účinnost znamená, že e max = 0,22, proto:
Maximální účinnost = práce / Qvstup
Množství absorbovaného tepla je přesné Qvstup, takže clearing máme:
Qvstup = Práce / Efektivita = 1530 J / 0,22 = 6954,5 J
b) Množství tepla přeneseného do nejchladnější nádrže se zjistí z ΔW = Qvstup - Qvýstup
Qvýstup = Qvstup - ΔŠ = 6954,5 - 1530 J = 5424,5 J.
Jiný způsob je z amax = 1 - (T.dva/ T1). Protože teploty nejsou známy, ale vztahují se k teplu, lze účinnost také vyjádřit jako:
amax = 1 - (Otázkaustoupil/ Qvstřebává)
Reference
- Bauer, W. 2011. Fyzika pro inženýrství a vědy. Svazek 1. Mc Graw Hill. 654-657
- Nukleární energie. Provoz jaderné elektrárny. Obnoveno z: energia-nuclear.net
- Serway, R., Jewett, J. (2008). Fyzika pro vědu a techniku. Svazek 1. 7. Ed. Cengage Learning. 618-622.
- Tippens, P. 2011. Fyzika: koncepty a aplikace. 7. vydání. MacGraw Hill. 414-416.
- Walker, J. 2008. Fyzika. 4. vyd. Addison Wesley. 610-630


Zatím žádné komentáře