
Pravidla významných čísel, příklady, řešená cvičení
Je pojmenován Významná čísla na počet číslic obsažených v mantisa čísla. Čím více čísel máte, tím přesněji je počet znám. Připomínáme, že mantisa je číslo, které doprovází mocninu 10, když je číslo napsáno vědeckou notací..
Vezměme si například číslo 0,00376, které je zapsáno jako 3,76 x 10 -3. Mantisa je 3,76 a číslo má celkem 3 platné číslice. Číslo 0,129 má také 3 platné číslice, zatímco číslo 4,5 má pouze 2.

A co se stane, když je číslo celé číslo? Znamená to, že je známo s co největší přesností, jinými slovy, má nekonečnou přesnost. Například při počítání lidí, zvířat nebo předmětů, jako jsou knihy a telefony, je výsledkem přesné celé číslo.
Pokud řekneme, že v kině sleduje film 110 lidí, je to přesný počet, ani více, ani méně, a má 3 významné postavy.
S významnými čísly se zachází některými jednoduchými pravidly, která si pamatujeme s trochou praxe, jak uvidíme níže..
Rejstřík článků
- 1 Pravidla pro určování platných číslic čísla
- 1.1 Pravidlo 1
- 1.2 Pravidlo 3
- 1.3 Pravidlo 4
- 1.4 Pravidlo 5
- 2 Příklady
- 2.1 Příklad 1
- 2.2 Příklad 2
- 2.3 Příklad 3
- 3 Pravidla pro zaokrouhlování čísel
- 4 Odkazy
Pravidla pro určování platných číslic čísla
Pravidlo 1
Počáteční nuly se nepočítají jako významné číslo, takže 0,045 a 4,5 mají 2 platné čísla, protože se začínají počítat zleva a začínají od první nenulové číslice.
Pravidlo 2
Nuly za (vpravo) první významnou číslicí se považují za významnou číslici (pokud je to odůvodněno přesností měřicího přístroje).
Nakonec se nuly ve středu také počítají jako významná číslice..
Pravidlo 3
U čísel zapsaných vědeckou notací jsou všechny číslice v mantisě významné a exponent neovlivňuje přesnost..
Pravidlo 4
Při provádění operací s desetinnými místy, například při výpočtu ploch nebo jiných podobných operací, musí mít výsledek stejný počet platných číslic jako množství s nejmenším počtem platných číslic, které se operace zúčastnily. Toto pravidlo platí pro jakoukoli aritmetickou operaci.
Pravidlo 5
Znaménko čísla neovlivňuje jeho počet platných čísel.
Okamžitě uvidíme několik příkladů tohoto a všech ostatních pravidel.
Příklady
Příklad 1
Zjistěte, kolik platných čísel je v každém z těchto čísel.
a) 876
b) 1000,68
c) 0,00005026
d) 4.8
e) -6,99
Odpovědi
a) 876 má 3 platné číslice.
b) 1000.68 má 6 platných čísel, protože nuly mezi nimi se jako takové počítají.
c) Místo toho má 0,00005026 4 platná čísla. Všimněte si, že 5 nul nalevo od 5 se nepočítá jako významná postava, místo toho je 0 mezi 5 a 2..
d) 4.8 má 2 platné číslice.
e) -6,99 má 3 platná čísla.
Příklad 2
Je běžné provádět měření pomocí měřicích přístrojů, jako jsou měřicí pásky, hodinky, teploměry, váhy atd. S kolika významnými čísly bychom měli hlásit množství, která měříme tímto způsobem??
Odpovědět
Závisí to na zhodnocení nástroje, kterým je měřeno. Vezměme si příklad: změřte vnější průměr trubice, s odměrným pravítkem a s noniem nebo posuvným měřítkem.
Vernier je nástroj, který měří délky velmi přesně, protože má extra malý rozsah zvaný nonius, což umožňuje měřit větší jemnost.
Je přesnější než odstupňované pravítko, protože s ním můžeme znát významnější postavy určité délky.
Proto nemá smysl hlásit obvod, řekněme, 35,88 cm, měříme-li jej páskovým měřičem, protože tento nástroj není dostatečně přesný, aby hlásil tolik platných číslic..
Ocenění A měřicího pásu je dáno:
Příklad 3
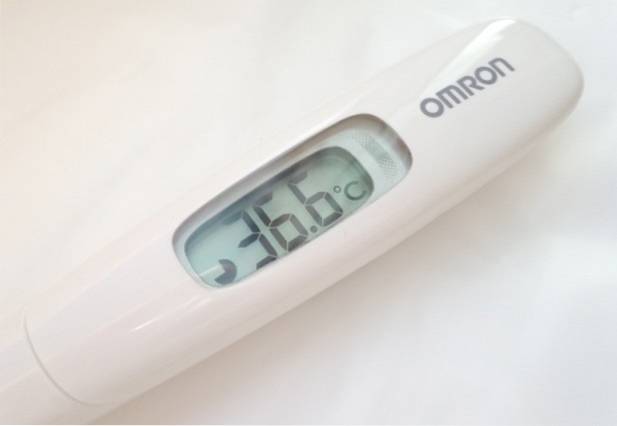
Kolik platných čísel má odečet provedený digitálním teploměrem?
Odpovědět
Teploměr na obrázku poskytuje tříciferné hodnoty teploty. U zobrazeného měření 36,6 ° C jsou však přesné pouze první dvě číslice zleva doprava, protože na desetinnou čárku má vliv chyba vyhodnocení přístroje, která je obvykle uvedena na zadní straně přístroje nebo v provozní příručce..
Obvyklá věc pro zobrazený typ digitálního přístroje je chyba vyhodnocení 0,1 ° C. To je dost pro jistotu, že nemáte horečku..

Pravidla pro zaokrouhlování čísel
Při použití kalkulačky k provádění výpočtů se získanými měřeními není správné dávat výsledek pomocí všech číslic, které se zobrazují na obrazovce.
Zachovány jsou pouze ty, které jsou přesně známy, protože pouze ty mají skutečný význam. Poté je nutné zaokrouhlit výsledky tak, aby odpovídaly počtu přesně známých čísel. Tato pravidla jsou:
-Pokud je číslo následující za zadržovanou číslicí rovna nebo větší než 5, 1 se přidá k této číslici.
Například při zaokrouhlování 3,786 na dvě desetinná místa chceme zachovat čísla až do 8. Jelikož číslo, které následuje (6), je větší než 5, 8 se stane 8 + 1 = 9 a číslo zůstane jako 3,79.
-Pokud je číslo následující za číslicí, která má být přidržena méně než 5, číslice zůstává stejná.
Pokud chceme zaokrouhlit 1,27924 tak, aby měla pouze 3 desetinná místa, dosáhneme toho dosažením 9, za nimiž následuje 2. Protože 2 je menší než 5, tato desetinná místa zmizí a zaokrouhlený počet zůstane 1,279.
Cvičení vyřešeno
Jídelní stůl má tvar a rozměry uvedené na přiloženém obrázku. Budete požádáni, abyste vypočítali jeho plochu pomocí provozních pravidel s významnými čísly.
Řešení
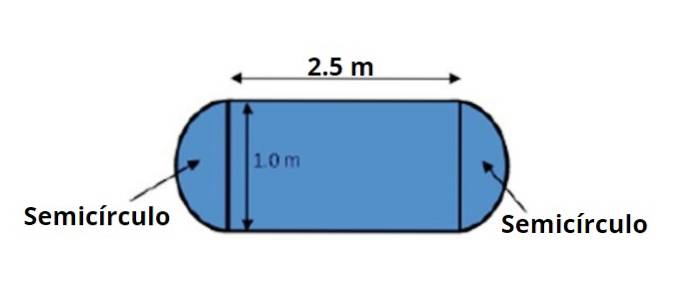
Plochu stolu lze rozdělit na střední obdélníkovou plochu a dva půlkruhy, jeden na každé straně, které dohromady tvoří 1 plný kruh.
Zavoláme A1 na plochu obdélníku danou vztahem:
NA1 = základna × výška = 2,5 m x 1,0 m = 2,5 mdva
Plocha kruhu, která se rovná ploše 1 půlkruhu vynásobeného 2, je:
NAdva = poloměr π ×dva
Průměr kteréhokoli z půlkruhů je 1,0 m, takže poloměr je 0,50 m. Průměr lze také použít přímo k výpočtu plochy, v tomto případě:
NAdva = (π × průměrdva) / 4
V každém případě:
NAdva = [π x (1,0 m)dva] / 4 = 0,785398163 mdva
Byly použity všechny číslice poskytnuté kalkulačkou. Nyní přidáme A.1 jiždva pro celkovou plochu A tabulky:
A = (2,5 + 0,785398163) mdva = 3,285398163 mdva
Jelikož rozměry tabulky jsou známy dvěma platným číslům, nemá smysl vyjadřovat výsledek se všemi desetinnými místy danými kalkulačkou, která nikdy neposkytuje počet platných číslic výsledku.
Musíte zaokrouhlit plochu tak, aby měla stejný počet platných čísel jako rozměry tabulky, tedy 2. Konečný výsledek se proto uvádí takto:
A = 3,3 mdva
Reference
- Bauer, W. 2011. Fyzika pro inženýrství a vědy. Svazek 1. Mc Graw Hill.
- Figueroa, D. (2005). Série: Fyzika pro vědu a techniku. Svazek 1. Kinematika. Upravil Douglas Figueroa (USB).
- Fisicalab. Významné údaje a zaokrouhlování. Obnoveno z: fisicalab.com.
- Giancoli, D. 2006. Fyzika: Principy s aplikacemi. 6.. Hala Ed Prentice.
- Sears, Zemansky. 2016. Univerzitní fyzika s moderní fyzikou. 14. Vydání Volume1.



Zatím žádné komentáře