Jak zjistit úhel trojúhelníku?

Existuje několik způsobů, jak vypočítat strany a úhly trojúhelníku. Ty závisí na typu trojúhelníku, se kterým pracujete.

V této příležitosti se ukáže, jak vypočítat strany a úhly pravoúhlého trojúhelníku za předpokladu, že některá data trojúhelníku se známými.

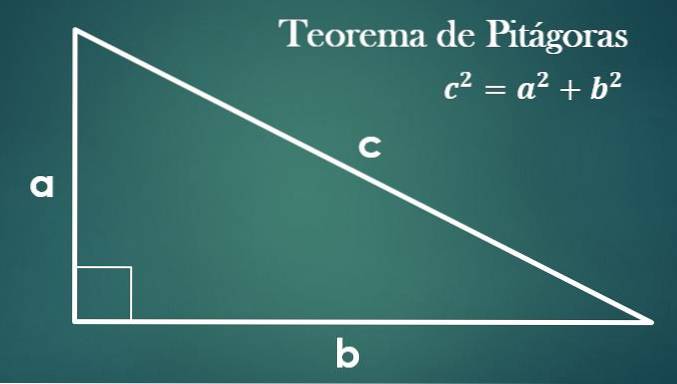
Budou použity tyto prvky:

- Pytagorova věta

Vzhledem k pravoúhlému trojúhelníku s nohami „a“, „b“ a přeponou „c“ platí, že „c² = a² + b²“.

- Plocha trojúhelníku

Vzorec pro výpočet plochy libovolného trojúhelníku je A = (b × h) / 2, kde „b“ je délka základny a „h“ je délka výšky.

- Úhly trojúhelníku

Součet tří vnitřních úhlů trojúhelníku je 180 °.

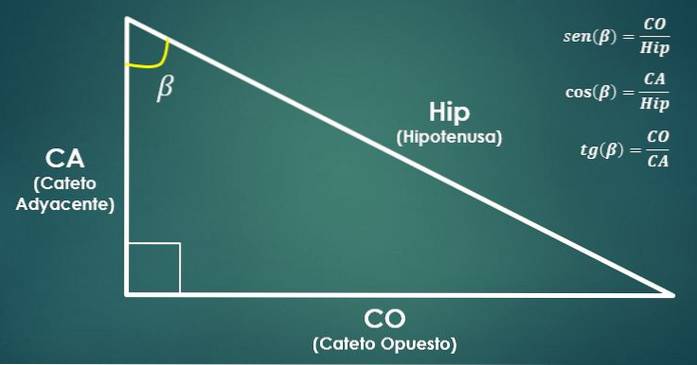
- Trigonometrické funkce:

Vezměme si pravý trojúhelník. Poté jsou trigonometrické funkce sinus, kosinus a tangenta úhlu beta (β) definovány takto:

sin (β) = CO / Hip, cos (β) = CA / Hip a tan (β) = CO / CA.

Jak najít strany a úhly pravoúhlého trojúhelníku?

Vzhledem k pravoúhlému trojúhelníku ABC může dojít k následujícím situacím:

1- Obě nohy jsou známé

Pokud noha „a“ měří 3 cm a noha „b“ měří 4 cm, pak se k výpočtu hodnoty „c“ použije Pythagorova věta. Dosazením hodnot „a“ a „b“ získáme, že c² = 25 cm², což znamená, že c = 5 cm.

Nyní, pokud je úhel β naproti noze „b“, pak sin (β) = 4/5. Použitím inverzní funkce sinu v této poslední rovnosti získáme, že β = 53,13 °. Dva vnitřní úhly trojúhelníku jsou již známy.

Nechť θ je úhel, který zbývá znát, pak 90 ° + 53,13 ° + θ = 180 °, ze kterého získáme, že θ = 36,87 °.

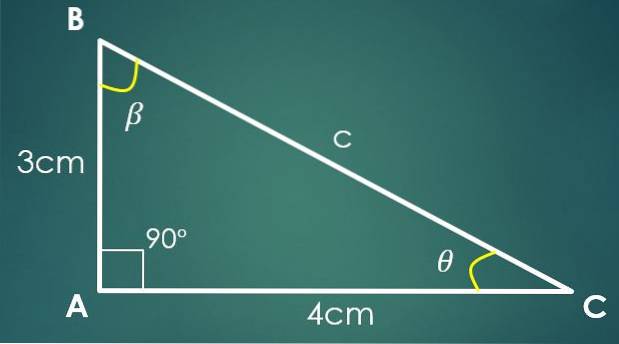
V tomto případě není nutné, aby známé strany byly obě nohy, důležité je znát hodnotu jakýchkoli dvou stran.

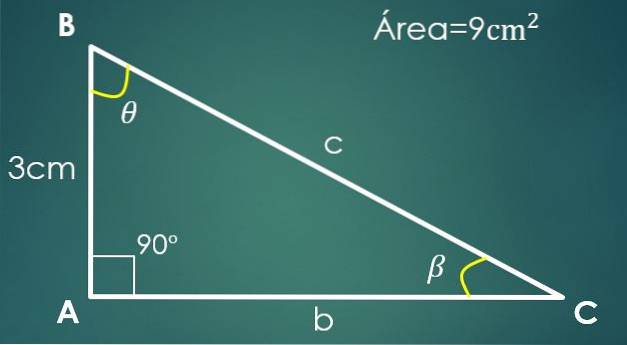
2- Je známa noha a oblast

Nechť a = 3 cm je známá noha a A = 9 cm² plocha trojúhelníku.

V pravoúhlém trojúhelníku lze jednu nohu považovat za základnu a druhou za výšku (protože jsou kolmé).

Předpokládejme, že „a“ je základna, tedy 9 = (3 × h) / 2, z čehož získáme, že druhá noha je 6 cm. Při výpočtu přepony postupujte jako v předchozím případě a získáme c = √45 cm.

Nyní, pokud je úhel β naproti noze „a“, pak sin (β) = 3 / √45. Při řešení pro β se získá, že jeho hodnota je 26,57 °. Potřebujeme znát pouze hodnotu třetího úhlu θ.

Je spokojeno, že 90 ° + 26,57 ° + θ = 180 °, z čehož se vyvozuje, že θ = 63,43 °.

3 - Jsou známy úhel a noha

Nechť β = 45 ° je známý úhel a a = 3 cm známá noha, kde noha „a“ je opačný úhel β. Pomocí tangenciálního vzorce získáme tg (45º) = 3 / CA, ze kterého vyplývá, že CA = 3 cm.

Pomocí Pythagorovy věty se získá, že c² = 18 cm², tj. C = 3√2 cm.

Je známo, že úhel měří 90 ° a že β měří 45 °, odtud se vyvozuje, že třetí úhel měří 45 °.

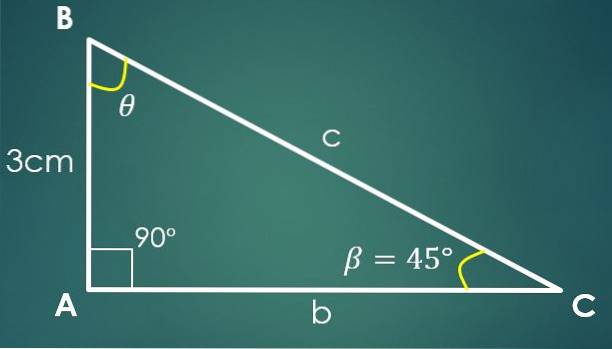
V tomto případě nemusí být známá strana nohou, může to být kterákoli ze tří stran trojúhelníku.

Reference

1. Landaverde, F. d. (1997). Geometrie (Dotisk ed.). Pokrok.
2. Leake, D. (2006). Trojúhelníky (ilustrované vydání). Heinemann-Raintree.
3. Pérez, C. D. (2006). Předpočet. Pearson Education.
4. Ruiz, Á., & Barrantes, H. (2006). Geometrie. CR technologie.
5. Sullivan, M. (1997). Předpočet. Pearson Education.
6. Sullivan, M. (1997). Trigonometrie a analytická geometrie. Pearson Education.