
Příklady obdélníkových souřadnic a řešená cvičení
The obdélníkové souřadnice nebo kartézské jsou ty, které se získají ortogonálním promítnutím na tři kartézské osy X, Y, Z bod umístěný v trojrozměrném prostoru.
Kartézské osy jsou vzájemně orientované přímky na sebe kolmé. V karteziánském souřadnicovém systému je každému bodu v prostoru přiřazena tři reálná čísla, což jsou jeho obdélníkové souřadnice.
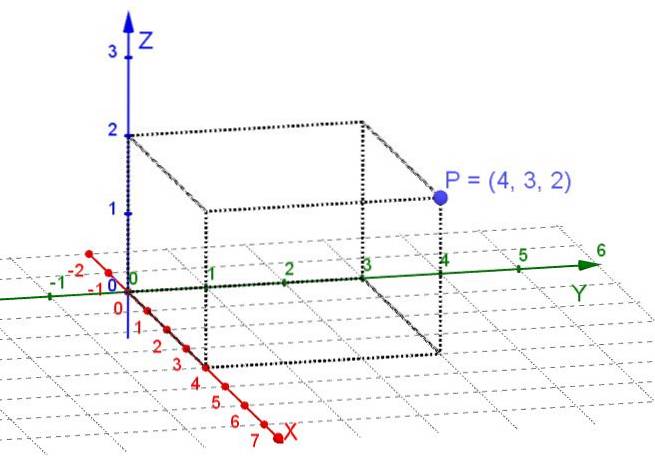
Rovina je podprostorem trojrozměrného prostoru. V případě uvažování bodů v rovině stačí zvolit dvojici kolmých os X, Y jako kartézský systém. Potom je každému bodu roviny přiřazena dvě reálná čísla, která jsou jeho obdélníkovými souřadnicemi.
Rejstřík článků
- 1 Počátek obdélníkových souřadnic
- 2 Kartézská rovina
- 2.1 Vzdálenost mezi dvěma body
- 2.2 Analytické vyjádření řádku
- 3 příklady
- 3.1 Příklad 1
- 3.2 Příklad 2
- 4 Vyřešená cvičení
- 4.1 Cvičení 1
- 4.2 Cvičení 2
- 5 Reference
Počátek obdélníkových souřadnic
Obdélníkové souřadnice původně navrhl francouzský matematik René Descartes (1596 a 1650), proto se jim říká kartézské.
S touto myšlenkou Descartes, body roviny a prostoru jsou přiřazena čísla, takže geometrické postavy mají algebraickou rovnici asociovanou a klasické geometrické věty lze algebraicky dokázat. S kartézskými souřadnicemi se rodí analytická geometrie.
Kartézská rovina
Pokud jsou v rovině zvoleny dvě kolmé čáry, které se protínají v bodě O; a pokud je navíc každé přímce přiřazen směr a číselná stupnice mezi po sobě jdoucími ekvidistantními body, pak existuje kartézský systém nebo rovina, ve které je každý bod roviny spojen s uspořádanou dvojicí dvou reálných čísel, které jsou jejich projekcemi respektive na osách X a Y..
Body A = (3, 2); B = (- 2, 3); C = (- 2, -3) a D = (3, -3) jsou reprezentovány v kartézské rovině, jak je znázorněno níže:
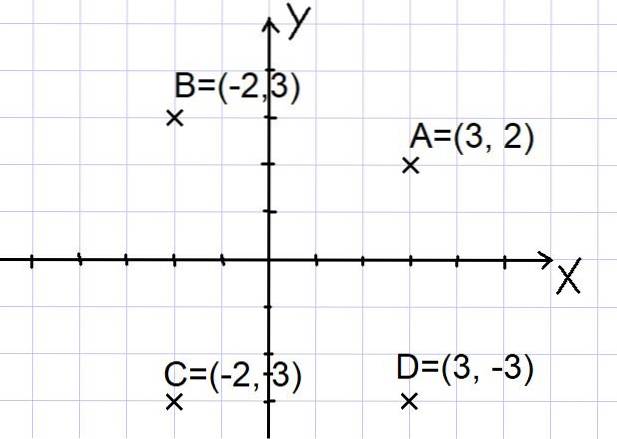
Všimněte si, že dvě osy X a Y rozdělují rovinu na čtyři sektory zvané kvadranty. Bod A je v prvním kvadrantu, B je ve druhém kvadrantu, C je ve třetím kvadrantu a bod D je ve čtvrtém kvadrantu..
Vzdálenost mezi dvěma body
Vzdálenost mezi dvěma body A a B na kartézské rovině je délka segmentu, který je spojuje. Tuto vzdálenost lze vypočítat analyticky následujícím způsobem:
d (A, B) = √ (Bx - Ax) ^ 2 + (By - Ay) ^ 2)
Výše uvedený vzorec se získá použitím Pythagorovy věty.
Aplikováním tohoto vzorce na body A, B na obrázku 2 máme:
d (A, B) = √ (-2 - 3) ^ 2 + (3 - 2) ^ 2) = √ (-5) ^ 2 + 1 ^ 2) = √ (26)
To znamená, d (A, B) = 5,10 jednotek. Všimněte si, že vzdálenost byla získána bez nutnosti měření pomocí pravítka, byl dodržen zcela algebraický postup.
Analytické vyjádření řádku
Obdélníkové souřadnice umožňují analytické znázornění základních geometrických objektů, jako jsou bod a přímka. Dva body A a B definují jednu linii. Sklon přímky je definován jako podíl mezi rozdílem souřadnic Y bodu B mínus A, děleným rozdílem souřadnic X bodu B mínus A:
sklon = (By - Ay) / (Bx - Axe)
Jakýkoli bod P souřadnic (x, y), který patří k přímce (AB), musí mít stejný sklon:
sklon = (y - Ay) / (x - Axe)
Rovnice, která se získá pomocí rovnosti svahů, je analytická nebo algebraická reprezentace přímky, která prochází body A a B:
(y - Ay) / (x - Ax) = (By - Ay) / (Bx - Ax).
Vezmeme-li pro A a B pravoúhlé souřadnice obrázku 2, máme:
(y - 2) / (x - 3) = (3 - 2) / (- 2 - 3)
(y - 2) / (x - 3) = -⅕
V tomto konkrétním případě máme přímku se záporným sklonem -⅕, což znamená, že umístěním bodu na přímce a zvýšením souřadnice x o jednu jednotku se souřadnice y sníží o 0,2 jednotky.
Nejběžnějším způsobem, jak zapsat rovnici přímky v rovině, je vymazání souřadnice y jako funkce proměnné x:
y = - (1/5) x + 13/5
Příklady
Příklad 1
Získejte analytickými metodami vzdálenost mezi body C a A, což jsou obdélníkové souřadnice C = (-2, -3) a A = (3,2).
Vzorec pro euklidovskou vzdálenost mezi těmito dvěma body je napsán takto:
d (A, C) = √ ((Cx - Ax) ^ 2 + (Cy - Ay) ^ 2)
Dosazením odpovídajících pravoúhlých souřadnic máme:
d (A, C) = √ (-2 - 3) ^ 2 + (-3 - 2) ^ 2) = √ (-5) ^ 2 + (-5) ^ 2) = 5√2 = 7,07
Příklad 2
Získejte rovnici přímky, která prochází bodem C souřadnic (-2, -3) a bodem P souřadnic (2, 0).
Nejprve se získá sklon přímky CP:
sklon = (0 - (- 3)) / (2 - (-2)) = ¾
Jakýkoli bod Q obecných obdélníkových souřadnic (x, y), který patří k přímce CP, musí mít stejný sklon:
sklon = (y - (- 3)) / (x - (-2)) = (y +3) / (x +2)
Jinými slovy, rovnice přímky CP je:
(y +3) / (x +2) = ¾
Alternativní způsob zápisu rovnice řádku CP je řešení pro y:
y = ¾ x - 3/2
Vyřešená cvičení
Cvičení 1
Získejte obdélníkové souřadnice průsečíku mezi přímkami y = - (1/5) x + 13/5 a přímkou y = ¾ x - 3/2.
Řešení: Podle definice sdílí průsečík dvou čar stejné obdélníkové souřadnice. Proto jsou souřadnice y v průsečíku shodné pro obě čáry:
-(1/5) x + 13/5 = ¾ x - 3/2
což vede k následujícímu výrazu:
(¾ + ⅕) x = 13/5 +3/2
řešením součtu zlomků získáme:
19/20 x = 41/10
Řešení pro x:
x = 82/19 = 4,32
Pro získání průsečíku y je dosažená hodnota x nahrazena v kterémkoli z řádků:
y = ¾ 4,32 - 3/2 = 1,74
To znamená, že se dané čáry protínají v bodě I souřadnic I = (4,32, 1,74).
Cvičení 2
Získejte rovnici obvodu, která prochází bodem R obdélníkových souřadnic (3, 4) a která má střed v počátku souřadnic.
Řešení: Poloměr R je vzdálenost od bodu R k počátku O souřadnic (0, 0).
d (R, O) = √ ((Rx - 0) ^ 2 + (Ry - 0) ^ 2) = √ ((3 - 0) ^ 2 + (4 - 0) ^ 2) = √ (3 ^ 2 + 4 ^ 2) = √ (9 + 16) = √ (25) = 5
To znamená, že se jedná o kruh o poloměru 5 se středem (0,0).
Libovolný bod P (x, y) na obvodu musí mít stejnou vzdálenost 5 od středu (0, 0), aby mohl být zapsán:
d (P, O) = √ ((x - 0) ^ 2 + (y - 0) ^ 2) = √ (x ^ 2 + y ^ 2) = 5
A to:
√ (x ^ 2 + y ^ 2) = 5
Abychom vyloučili druhou odmocninu, oba členové rovnosti jsou čtvercoví a získají:
x ^ 2 + y ^ 2 = 25
Jaká je rovnice obvodu.
Tento příklad ilustruje sílu obdélníkového souřadnicového systému, který umožňuje určovat geometrické objekty, například obvod, bez nutnosti použití papíru, tužky a kompasu. Požadovaný obvod byl určen pouze algebraickými metodami.
Reference
- Arfken G a Weber H. (2012). Matematické metody pro fyziky. Komplexní průvodce. 7. vydání. Akademický tisk. ISBN 978-0-12-384654-9
- Výpočet cc. Vyřešené úlohy pravoúhlých souřadnic. Obnoveno z: Calclo.cc
- Weisstein, Eric W. "Kartézské souřadnice." Z webu MathWorld-A Wolfram. Obnoveno z: mathworld.wolfram.com
- wikipedia. Kartézský souřadnicový systém. Obnoveno z: en.wikipedia.com



Zatím žádné komentáře