
Jaké jsou 3 prvky vektoru?
The prvky vektoru jsou to směr, vzdálenost a modul. V matematice, fyzice a inženýrství je vektor geometrický objekt, který má velikost (nebo délku) a směr. Podle vektorové algebry lze vektory přidávat k jiným vektorům.
K získání bodu A do bodu B je zapotřebí vektor. Vektory hrají ve fyzice důležitou roli: rychlost a zrychlení pohybujícího se objektu a síly na něj působící lze popsat pomocí vektorů..
Mnoho dalších fyzikálních vlastností lze považovat za vektory. Matematické znázornění fyzického vektoru závisí na souřadném systému použitém k jeho popisu..
Existuje několik tříd vektorů, mezi nimi najdeme mimo jiné posuvné vektory, kolineární vektory, souběžné vektory, vektory polohy, volné vektory, paralelní vektory a koplanární vektory..
Prvky vektoru
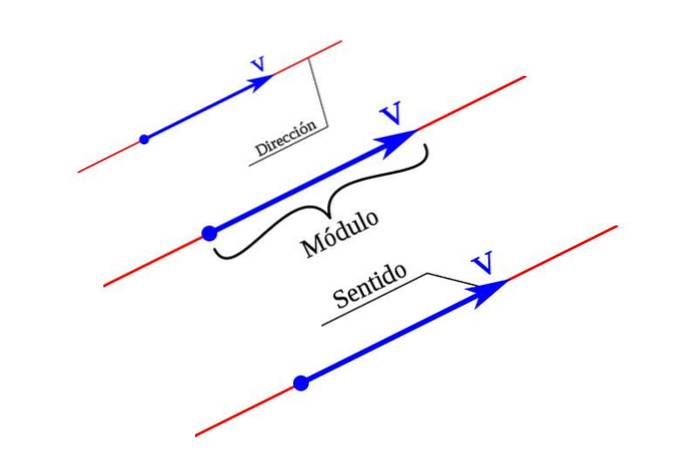
Vektor má hlavně tři prvky: směr, smysl a modul.
Vektor je entita, která má velikost i směr. Mezi příklady vektorů patří posunutí, rychlost, zrychlení a síla. K popisu jedné z těchto vektorových veličin je nutné zjistit velikost a směr.
Například pokud je rychlost objektu 25 metrů za sekundu, pak je popis rychlosti objektu neúplný, protože objekt se může pohybovat rychlostí 25 metrů za sekundu na jih nebo 25 metrů za sekundu na sever, nebo 25 metrů za sekundu na jihovýchod.
Aby bylo možné plně popsat rychlost objektu, musí být definovány oba: jak rychlost 25 metrů za sekundu, tak směr, jako je jih.
Aby byly takovéto popisy vektorových veličin užitečné, je důležité, aby se všichni shodli na tom, jak je popsán směr objektu..
Většina lidí je zvyklá na myšlenku, že při pohledu doprava je východní směr označován na mapě. Ale toto je pouhá konvence, kterou tvůrci map používají už léta, aby každý mohl souhlasit..
Jaký je tedy směr vektorové veličiny, která nemíří na sever nebo na východ, ale někde mezi severem a východem? Pro tyto případy je důležité, aby existovala konvence popisující směr uvedeného vektoru.
Tato konvence se označuje jako CCW. Pomocí této konvence můžeme popsat směr libovolného vektoru z hlediska jeho úhlu otáčení doleva..
Při použití této konvence by byl severní směr 90 °, protože pokud by vektor směřoval na východ, musel by se otočit o 90 ° doleva, aby se dosáhlo severního bodu..
Stejně tak by se směr na západ nacházel na 180 °, protože vektor směřující na západ by musel být otočen o 180 ° doleva, aby ukazoval na západ..
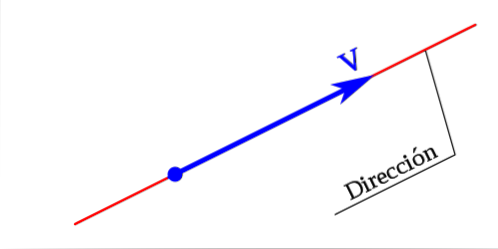
Jinými slovy, směr vektoru bude představován přímkou obsaženou ve vektoru nebo jakoukoli přímkou, která je s ním rovnoběžná.,
Bude určeno úhlem vytvořeným mezi vektorem a jakoukoli jinou referenční čarou. To znamená, že směr čáry, která je ve vektoru, nebo nějaká čára rovnoběžná s ním, je směr vektoru.
Smysl
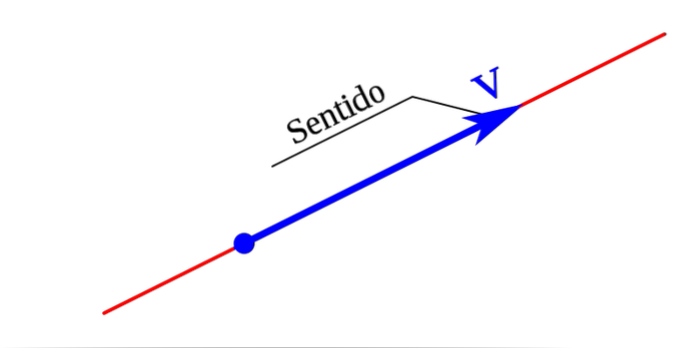
Smysl vektoru odkazuje na prvek, který popisuje, jak bod A končí na konci B:
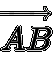
Směr vektoru je určen řádem dvou bodů na přímce rovnoběžné s vektorem, na rozdíl od směru vektoru, který je určen vztahem mezi vektorem a jakoukoli referenční přímkou a / nebo rovinou..
Orientace i směr určují směr vektoru. Orientace udává, v jakém úhlu je vektor, a smysl určuje, kam směřuje..
Směr vektoru určuje pouze úhel, který vektor vytváří se svou vodorovnou osou, ale který může vytvářet nejednoznačnost, protože šipka může ukazovat ve dvou opačných směrech a stále dělat stejný úhel.
Smysl tuto nejednoznačnost vymaže a naznačuje, kam směřuje šipka nebo kam směřuje vektor..
Smysl nám nějak říká, v jakém pořadí číst vektor. Označuje, kde vektor začíná a končí.
Modul
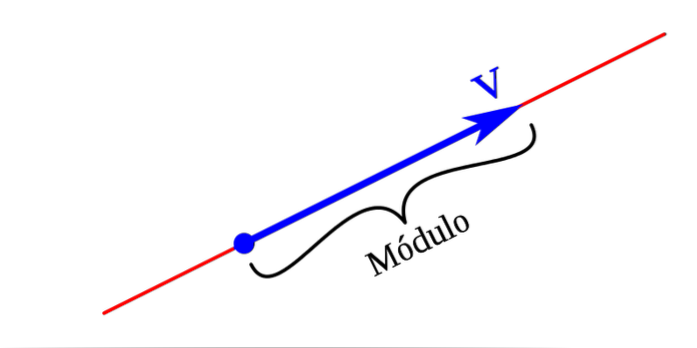
Modul nebo amplitudu vektoru lze definovat jako délku segmentu AB. Modul může být reprezentován délkou, která je úměrná hodnotě vektoru. Modul vektoru bude vždy nula, nebo v jiných případech nějaké kladné číslo.
V matematice bude vektor definován jeho euklidovskou vzdáleností (modulem), směrem a smyslem.
Euklidovská vzdálenost nebo euklidovská vzdálenost je „běžná“ vzdálenost v přímce mezi dvěma body umístěnými v euklidovském prostoru. S touto vzdáleností se euklidovský prostor stává metrickým prostorem.
Euklidovská vzdálenost mezi dvěma body, například P a Q, je vzdálenost mezi úsečkou, která je spojuje:

Poloha bodu v euklidovském prostoru n je vektor. P a Q jsou tedy vektory, počínaje počátkem prostoru a jejich body označující dva body.
Euklidovská norma, velikost nebo euklidovská vzdálenost vektoru měří délku tohoto vektoru.
Reference
- Vektorový směr. Obnoveno z physicsclassroom.com.
- Jaký je smysl vektoru? Obnoveno z physics.stackexchange.com.
- Jaký je rozdíl mezi směrem, smyslem a orientací? Obnoveno z math.stackexchange.com.
- Euklidovská vzdálenost. Obnoveno z wikipedia.org.



Zatím žádné komentáře