Co jsou dělitelé 30?

Rychle to lze zjistit jaké jsou dělitele 30, stejně jako jakékoli jiné číslo (jiné než nula), ale základní myšlenkou je naučit se, jak se dělitele čísla počítají obecně.

Když mluvíme o dělitelích, musíme být opatrní, protože lze rychle zjistit, že všechny dělitele 30 jsou 1, 2, 3, 5, 6, 10, 15 a 30, ale co negativa těchto čísel? Jsou to rozdělovače nebo ne?

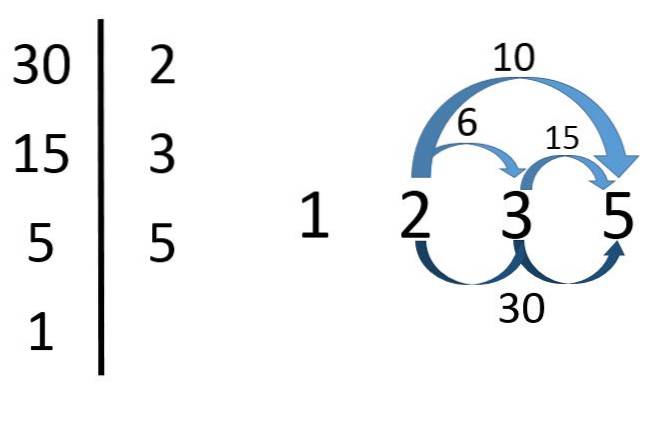
Pro zodpovězení předchozí otázky je nutné pochopit velmi důležitý pojem ve světě matematiky: algoritmus dělení.

Algoritmus dělení

Algoritmus dělení (nebo euklidovské dělení) říká toto: vzhledem k tomu, že dvě celá čísla „n“ a „b“, kde „b“ se liší od nuly (b ≠ 0), existují pouze celá čísla „q“ a „r“, například že n = bq + r, kde 0 ≤ r < |b|.

Číslo „n“ se nazývá dividenda, „b“ se dělí, „q“ se nazývá kvocient a „r“ se označuje zbytek nebo zbytek. Když je zbytek „r“ roven 0, říká se, že „b“ rozděluje „n“, a to je označeno „b | n“.

Algoritmus dělení není omezen na kladné hodnoty. Proto záporné číslo může být dělitelem nějakého jiného čísla.

Proč 7.5 není dělitelem 30??

Pomocí algoritmu dělení je vidět, že 30 = 7,5 × 4 + 0. Zbytek se rovná nule, ale nelze říci, že 7,5 dělí 30, protože když mluvíme o dělitelích, mluvíme jen o celých číslech.

Dělitelé 30

Jak je vidět na obrázku, k nalezení dělitele 30 je třeba nejprve najít jeho hlavní faktory.

Takže 30 = 2x3x5. Z toho usuzujeme, že 2, 3 a 5 jsou děliteli 30. Ale stejně tak i produkty těchto hlavních faktorů.

Takže 2 × 3 = 6, 2 × 5 = 10, 3 × 5 = 15 a 2x3x5 = 30 jsou děliteli 30. 1 je také dělitelem 30 (i když je to vlastně dělitel libovolného čísla).

Lze vyvodit závěr, že 1, 2, 3, 5, 6, 10, 15 a 30 jsou děliteli 30 (všechny odpovídají algoritmu dělení), ale je třeba si uvědomit, že jejich negativy jsou také děliteli.

Proto jsou všechny děliče 30: -30, -15, -10, -6, -5, -3, -2, -1, 1, 2, 3, 5, 6, 10, 15 a 30.

To, co jsme se naučili výše, lze použít na jakékoli celé číslo.

Například pokud chcete vypočítat dělitele 92, postupujte jako dříve. Rozkládá se jako produkt prvočísel.

Rozdělte 92 na 2 a získejte 46; nyní vydělte 46 znovu 2 a získejte 23.

Tento poslední výsledek je prvočíslo, takže nebude mít více dělitelů kromě 1 a stejných 23.

Pak můžeme napsat 92 = 2x2x23. Stejně jako dříve se dospělo k závěru, že 1,2,4,46 a 92 jsou děliteli 92.

Nakonec jsou negativy těchto čísel zahrnuty v předchozím seznamu, s nímž je seznam všech dělitelů 92 -92, -46, -4, -2, -1, 1, 2, 4, 46, 92.

Reference

1. Barrantes, H., Díaz, P., Murillo, M., & Soto, A. (1988). Úvod do teorie čísel. San José: EUNED.
2. Bustillo, A. F. (1866). Matematické prvky. Imp. Santiaga Aguada.
3. Guevara, M. H. (s.f.). Teorie čísel. San José: EUNED.
4. J., A. C. a A., L. T. (1995). Jak rozvíjet matematické logické uvažování. Santiago de Chile: Redakční Universitaria.
5. Jiménez, J., Delgado, M., & Gutiérrez, L. (2007). Průvodce Think II. Prahové edice.
6. Jiménez, J., Teshiba, M., Teshiba, M., Romo, J., Álvarez, M., Villafania, P., Nesta, B. (2006). Matematika 1 Aritmetika a předalgebra. Prahové edice.
7. Johnsonbaugh, R. (2005). Diskrétní matematika. Pearson Education.