
Implicitní deriváty, jak jsou řešeny a cvičení řešeny
The implicitní deriváty Jsou to nástroje používané v diferenciační technice aplikované na funkce. Používají se, když není možné v rámci běžných metod vymazat závislou proměnnou, která má být odvozena. Tato vůle se provádí na základě nezávislé proměnné.
Například ve výrazu 3xy3 - 2y + xydva = xy, nemůžete získat výraz, který definuje „y“ jako funkci „x“. Takže odvozením diferenciální exprese lze získat dy / dx.

Rejstřík článků
- 1 Jak se řeší implicitní deriváty??
- 2 Pravidlo řetězu
- 3 Provozní řád
- 4 Implicitní funkce
- 5 Historie
- 6 Aplikace
- 7 Vyřešená cvičení
- 7.1 Cvičení 1
- 7.2 Cvičení 2
- 8 Reference
Jak jsou řešeny implicitní deriváty?
Abychom vyřešili implicitní derivaci, začneme implicitním výrazem. Například: 3xy3 - 2y + xydva - xy = 0. Toto již bylo správně vyřešeno, není to však nutná podmínka pro získání derivace y vzhledem k x. Poté je každý z prvků odvozen s ohledem na pravidlo řetězu pro smíšené funkce:
3xy3 se skládá ze 2 proměnných, proto d (3xy3) bude považováno za derivát produktu funkcí.
d (3xy3) / dx = 3r3 + 3 rokydva.(3x) y '= 3r3 + 9xydva Y '
Kde je prvek y 'známý jako „a bratranec„Y představuje dy / dx
-2y Odvozuje se podle zákona K.U = K.U '
d (-2r) = -2 r.
xydva předpokládá další diferenciál složený z produktu funkcí
d (xydva) = adva + 2xy a '
-x a je zpracováno homologně
d (-xy) = -y - x y '
Jsou nahrazeny rovností, protože věděli, že derivace nuly je nula.
3 roky3 + 9xydva y '- 2 y' + ydva + 2xy y '- y - x y' = 0
Prvky, které mají výraz y ', jsou seskupeny na jedné straně rovnosti
3 roky3 + Ydva - y = -9xydva y '+ 2 y' + x y '
Společný faktor y 'je extrahován na pravé straně rovnosti
3 roky3 + Ydva - y = y '(-9xydva + x + 2)
Nakonec je termín, který znásobuje y 'zrušen. Tak získáme výraz odpovídající implicitní derivaci y vzhledem k x.
y '= dy / dx = (3r3 + Ydva - y) / (- 9xydva + x + 2)
Řetězové pravidlo
Při implicitní derivaci je vždy respektováno pravidlo řetězu. Všechny diferenciální výrazy budou uvedeny jako funkce nezávislé proměnné X. Takže každá proměnná θ jiná než X, musí po odvození obsahovat termín dθ / dx.
Tento termín se objeví pouze v prvním stupni nebo s exponentem rovným 1. Tato kvalita to při tradičních faktoringových metodách zcela objasňuje. Je tedy možné získat výraz, který definuje rozdíl dθ / dx.
Pravidlo řetězu ukazuje progresivní povahu procesu diferenciace nebo derivace. Kde pro každou složenou funkci f [g (x)] máme, že diferenciální výraz f bude
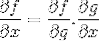
Provozní řád
V každém použitém vzorci nebo derivačním právu je třeba vzít v úvahu pořadí proměnných mezi sebou. Kritéria spojená s nezávislou proměnnou jsou respektována, aniž by se měnila její korelace se závislou proměnnou..
Vztah závislé proměnné v době derivace je převzat přímo; s výjimkou, že to bude považováno za druhou funkci, a proto se pro smíšené funkce použije kritérium řetězového pravidla.
To lze vyvinout ve výrazech s více než 2 proměnnými. Na základě stejných principů budou označeny všechny diferenciály odkazující na závislé proměnné.
Graficky je zpracováno stejné kritérium, které definuje derivaci. Zatímco derivací je sklon tečny k křivce v rovině, zbytek diferenciálů patřících k závislým proměnným (dy / dx, dz / dx) představuje roviny tečné k vektorovým tělesům popsaným více proměnnými funkcemi.
Implicitní funkce
O funkci se říká, že je implicitně definována, pokud lze výraz y = f (x) reprezentovat jako funkci více proměnných F (x, y) = 0, pokud je F definováno v rovině Rdva.
3xy3 - 2y + xydva = xy lze psát ve tvaru 3xy3 - 2y + xydva - xy = 0
Vzhledem k nemožnosti explicitní funkce y = f (x).
Příběh
Diferenciální počet začal být pojmenován různými matematickými vědci kolem sedmnáctého století. Poprvé to bylo zmíněno prostřednictvím příspěvků Newtona a Leibnize. Oba zacházeli s diferenciálním počtem z různých úhlů pohledu, ale ve svých výsledcích se sbíhali.
Zatímco Newton se soustředil na diferenciaci jako rychlost nebo rychlost změny, Leibnizův přístup byl více geometrický. Dá se říci, že Newton zaútočil na domněnky, které zanechal Apollonius z Perge a Leibniz, geometrické myšlenky Fermata.
Implicitní derivace se objeví okamžitě při zvažování diferenciálních a integrálních rovnic. Tyto rozšířily Leibnizův geometrický koncept na R.3 a dokonce vícerozměrné prostory.
Aplikace
Implicitní deriváty se používají v různých situacích. Jsou běžné v problémech směnných kurzů mezi souvisejícími proměnnými, kde v závislosti na smyslu studie budou proměnné považovány za závislé nebo nezávislé..
Mají také zajímavé geometrické aplikace, například v problémech s odrazem nebo stínem, na obrázcích, jejichž tvar lze matematicky modelovat..
Často se používají v oblastech ekonomiky a inženýrství, stejně jako při různých výzkumech přírodních jevů a experimentálních budovách..
Vyřešená cvičení
Cvičení 1
Definujte implicitní výraz, který definuje dy / dx
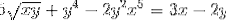
Každý prvek výrazu je diferencovaný
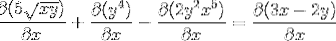
Stanovení řetězového pravidla v každém příslušném případě
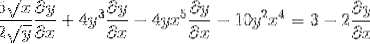
Seskupení na jedné straně rovnosti prvků, které mají dy / dx
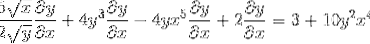
Je to započítáno pomocí společného faktoru
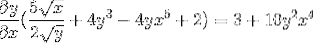
Je vyřešeno získání hledaného výrazu
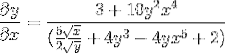
Cvičení 2
Definujte implicitní výraz, který definuje dy / dx
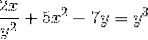
Vyjádření derivátů, které mají být provedeny
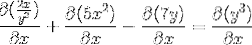
Odvození implicitně podle pravidla řetězu
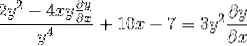
Faktorování společných prvků
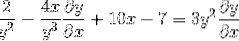
Seskupení termínu dy / dx na jedné straně rovnosti
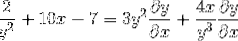
Společný faktor diferenciálního prvku
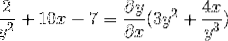
Izolujeme a získáváme hledaný výraz
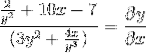
Reference
- Počet jedné proměnné. Ron Larson, Bruce H. Edwards. Cengage Learning, 10. listopadu 2008
- Věta o implicitní funkci: historie, teorie a aplikace. Steven G. Krantz, Harold R. Parks. Springer Science & Business Media, 9. listopadu. 2012
- Analýza více proměnných. Satish Shirali, Harkrishan Lal Vasudeva. Springer Science & Business Media, 13. prosince. 2010
- Systémová dynamika: modelování, simulace a řízení mechatronických systémů. Dean C. Karnopp, Donald L. Margolis, Ronald C. Rosenberg. John Wiley & Sons, 7. března 2012
- Matematika a modelování. William Bauldry, Joseph R. Fiedler, Frank R. Giordano, Ed Lodi, Rick Vitray. Addison Wesley Longman, 1. ledna 1999



Zatím žádné komentáře