Demonstrace nerovnosti trojúhelníku, příklady, řešená cvičení

To se nazývá nerovnost trojúhelníku na vlastnost dvou reálných čísel, která spočívá v tom, že absolutní hodnota jejich součtu je vždy menší nebo rovna součtu jejich absolutních hodnot. Tato vlastnost je také známá jako Minkowského nerovnost nebo trojúhelníková nerovnost.

Tato vlastnost čísel se nazývá trojúhelníková nerovnost, protože v trojúhelnících se stává, že délka jedné strany je vždy menší nebo rovna součtu ostatních dvou, i když tato nerovnost nemusí vždy platit v oblasti trojúhelníků..

Existuje několik důkazů trojúhelníkové nerovnosti v reálných číslech, ale v tomto případě si vybereme jeden na základě vlastností absolutní hodnoty a binomického čtverce.

Teorém: Pro každou dvojici čísel na Y b týkající se reálných čísel musí:

| a + b | ≤ | do | + | b |

Rejstřík článků

• 1 Ukázka
• 2 Příklady
  • 2.1 Příklad 1
  • 2.2 Příklad 2
  • 2.3 Příklad 3
  • 2.4 Příklad 4
  • 2.5 Příklad 5
  • 2.6 Příklad 6
• 3 Vyřešená cvičení
  • 3.1 Cvičení 1
  • 3.2 Cvičení 2
  • 3.3 Cvičení 3
  • 3.4 Cvičení 4
• 4 Odkazy

Demonstrace

Začneme zvážením prvního člena nerovnosti, který bude na druhou:

| a + b | ^ 2 = (a + b) ^ 2 = a ^ 2 + 2 a b + b ^ 2 (rovnice 1)

V předchozím kroku jsme použili vlastnost, že libovolné číslo na druhou se rovná absolutní hodnotě uvedeného čísla na druhou, tj.: | x | ^ 2 = x ^ 2. Rovněž byl použit vývoj čtvercového dvojčlenu.

Celé číslo X je menší nebo roven jeho absolutní hodnotě. Pokud je číslo kladné, je stejné, ale pokud je číslo záporné, bude vždy menší než kladné číslo. V tomto případě jeho vlastní absolutní hodnota, to znamená, že lze konstatovat, že x ≤ | x |.

Produkt (a b) je číslo, proto platí, že (a b) ≤ | a b |. Když je tato vlastnost aplikována na (Rov. 1), máme:

| a + b | ^ 2 = a ^ 2 + 2 (a b) + b ^ 2 ≤ a ^ 2 + 2 | a b | + b ^ 2 (rovnice 2)

S přihlédnutím k tomu | a b | = | a || b | (Rov. 2) lze napsat následovně:

 | a + b | ^ 2 ≤ a ^ 2 + 2 | a || b | + b ^ 2 (rovnice 3)

Ale protože jsme již dříve řekli, že čtverec čísla se rovná absolutní hodnotě čísla na druhou, pak rovnici 3 lze přepsat takto:

 | a + b | ^ 2 ≤ | a | ^ 2 + 2 | a | | b | + | b | ^ 2 (rovnice 4)

U druhého člena nerovnosti je rozpoznán pozoruhodný produkt, který při aplikaci vede k:

 | a + b | ^ 2 ≤ (| a | + | b |) ^ 2 (rovnice 5)

V předchozím výrazu je třeba poznamenat, že hodnoty, které mají být na druhou v obou členech nerovnosti, jsou kladné, proto je třeba se také ujistit, že:

 | a + b | ≤ (| a | + | b |) (rovnice 6)

Výše uvedený výraz je přesně to, co se chtělo demonstrovat.

Příklady

Dále zkontrolujeme trojúhelníkovou nerovnost s několika příklady.

Příklad 1

Vezmeme hodnotu a = 2 a hodnotu b = 5, tj. Obě kladná čísla a zkontrolujeme, zda je nerovnost uspokojena nebo ne.

 | 2 + 5 | ≤ | 2 | + | 5 |

 | 7 | ≤ | 2 | + | 5 |

7 ≤ 2+ 5

Rovnost je ověřena, proto byla splněna věta o nerovnosti trojúhelníku.

Příklad 2

Následující hodnoty jsou vybrány a = 2 a b = -5, tj. Kladné číslo a další záporné, zkontrolujeme, zda je nerovnost splněna nebo ne.

 | 2 - 5 | ≤ | 2 | + | -5 |

 | -3 | ≤ | 2 | + | -5 |

 3 ≤ 2 + 5

Nerovnost je splněna, proto byla ověřena věta o trojúhelníkové nerovnosti.

Příklad 3

Vezmeme hodnotu a = -2 a hodnotu b = 5, tj. Záporné číslo a druhou kladnou, zkontrolujeme, zda je nerovnost uspokojena nebo ne.

 | -2 + 5 | ≤ | -2 | + | 5 |

 | 3 | ≤ | -2 | + | 5 |

 3 ≤ 2 + 5

Nerovnost je ověřena, proto byla věta splněna.

Příklad 4

Následující hodnoty jsou vybrány a = -2 a b = -5, tj. Jak záporná čísla, tak zkontrolujeme, zda je nerovnost splněna nebo ne.

 | -2 - 5 | ≤ | -2 | + | -5 |

 | -7 | ≤ | -2 | + | -5 |

 7 ≤ 2+ 5

Rovnost je ověřena, proto byla Minkowského věta o nerovnosti splněna.

Příklad 5

Vezmeme hodnotu a = 0 a hodnotu b = 5, tj. Číslo nula a druhou kladnou, pak zkontrolujeme, zda je nerovnost splněna nebo ne.

 | 0 + 5 | ≤ | 0 | + | 5 |

 | 5 | ≤ | 0 | + | 5 |

 5 ≤ 0+ 5

Rovnost je splněna, proto byla ověřena věta o nerovnosti trojúhelníků.

Příklad 6

Vezmeme hodnotu a = 0 a hodnotu b = -7, tj. Číslo nula a druhé kladné, pak zkontrolujeme, zda je nerovnost splněna nebo ne.

 | 0 - 7 | ≤ | 0 | + | -7 |

 | -7 | ≤ | 0 | + | -7 |

 7 ≤ 0+ 7

Rovnost je ověřena, proto byla splněna věta o trojúhelníkové nerovnosti.

Vyřešená cvičení

V následujících cvičeních reprezentujte geometricky nerovnost trojúhelníku nebo Minkowského nerovnost pro čísla a a b.

Číslo a bude reprezentováno jako segment na ose X, jeho počátek O se shoduje s nulou osy X a druhý konec segmentu (v bodě P) bude v kladném směru (napravo) od Osa X, pokud a> 0, ale pokud a < 0 estará hacia la dirección negativa del eje X, tantas unidades como indique su valor absoluto.

Podobně bude číslo b reprezentováno jako segment, jehož počátek je v bodě P. Druhý extrém, tj. Bod Q bude napravo od P, pokud b bude kladné (b> 0) a bod Q bude | b | jednotky nalevo od P, pokud b<0.

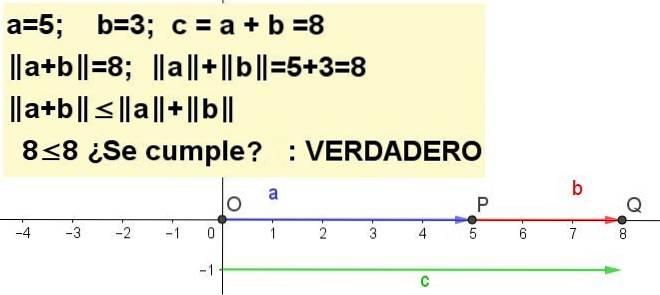
Cvičení 1

Graf nerovnice trojúhelníku pro a = 5 a b = 3 | a + b | ≤ | do | + | b |, bytost c = a + b. 

Cvičení 2

Graf trojúhelníkové nerovnosti pro a = 5 a b = -3. 

| a + b | ≤ | do | + | b |, bytost c = a + b.

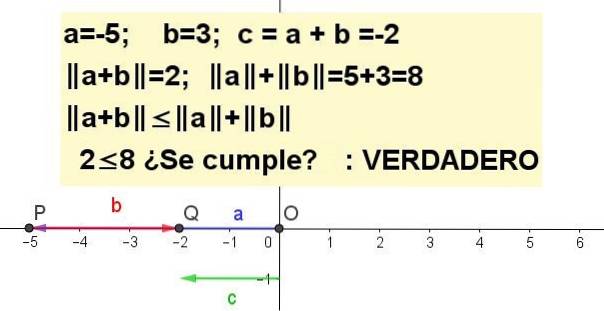
Cvičení 3

Graficky zobrazte nerovnost trojúhelníku pro a = -5 a b = 3.

| a + b | ≤ | do | + | b |, bytost c = a + b. 

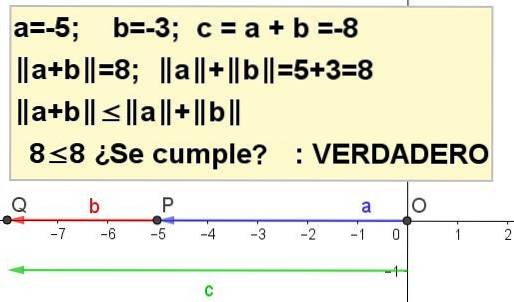
Cvičení 4

Graficky vytvořte trojúhelníkovou nerovnost pro a = -5 a b = -3.

| a + b | ≤ | do | + | b |, bytost c = a + b.

Reference

1. E. Whitesitt. (1980). Booleova algebra a její aplikace. Redakční společnost Continental C. A.
2. Mícheál O 'Searcoid. (2003) Prvky abstraktní analýzy… Katedra matematiky. University College Dublin, Beldfield, Dublind.
3. J. Van Wyk. (2006) Mathematics and Engineering in Computer Science. Institute for Computer Sciences and Technology. Národní úřad pro standardy. Washington, DC 20234
4. Eric Lehman. Matematika pro informatiku. Google Inc..
5. F Thomson Leighton (1980). Počet. Katedra matematiky a výpočetní techniky a laboratoře AI, Massachusetts Institute of Technology.
6. Khan Academy. Věta o nerovnosti trojúhelníku. Obnoveno z: khanacademy.org
7. Wikipedia. Trojúhelníková nerovnost. Obnoveno z: es. wikipedia.com