
Moody diagram rovnice, k čemu to je, aplikace
The náladový diagram sestává ze série křivek nakreslených na logaritmickém papíře, které se používají k výpočtu součinitele tření přítomného v toku turbulentní kapaliny kruhovým potrubím.
S koeficientem tření F je hodnocena ztráta energie třením, což je důležitá hodnota pro určení správného výkonu čerpadel, která distribuují kapaliny, jako je voda, benzín, ropa a další.

Chcete-li znát energii v toku tekutiny, je nutné znát zisky a ztráty způsobené faktory, jako jsou rychlost, výška, přítomnost zařízení (čerpadla a motory), účinky viskozity tekutiny a tření mezi ní a stěny potrubí.
Rejstřík článků
- 1 Rovnice pro energii tekutiny v pohybu
- 1,1 - Třecí faktor a Reynoldsovo číslo
- 2 K čemu to je?
- 3 Jak se vyrábí a jak se používá?
- 3.1 - Pracoval příklad 1
- 4 Aplikace
- 4.1 - Vyřešený příklad 2
- 5 Reference
Rovnice pro energii pohybující se tekutiny
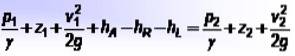
- p1 Y pdva jsou tlaky v každém bodě,
- z1 Y zdva jsou výšky vzhledem k referenčnímu bodu,
- proti1 Y protidva jsou příslušné rychlosti tekutin,
- hNA je energie přidaná čerpadly, hR je energie odebraná některým zařízením, například motorem, a hL pokrývá ztráty energie kapaliny v důsledku tření mezi kapalinou a stěnami potrubí a také další drobné ztráty.
Hodnota hL se vypočítá pomocí Darcy-Weisbachovy rovnice:
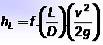
Kde L je délka potrubí, D je jeho vnitřní průměr, proti je rychlost tekutiny a G je hodnota gravitačního zrychlení. Rozměry hL jsou délka a obvykle jednotkami, ve kterých je znázorněna, jsou metry nebo stopy.
-Faktor tření a Reynoldsovo číslo
Vypočítat F lze použít empirické rovnice získané z experimentálních dat. Je nutné rozlišovat, zda se jedná o tekutinu v laminárním režimu nebo v turbulentním režimu. Pro laminární režim F snadno vyhodnotit:
f = 64 / NR
Kde NR je Reynoldsovo číslo, jehož hodnota závisí na režimu, ve kterém je tekutina. Kritériem je:
Laminární tok: NR < 2000 el flujo es laminar; Flujo turbulento NR > 4000; Přechodný režim: 2000 < NR < 4000
Reynoldsovo číslo (bezrozměrné) zase závisí na rychlosti kapaliny proti, vnitřní průměr trubky D a kinematická viskozita n kapaliny, jejíž hodnota se získá pomocí tabulek:
NR = v.D / n
Colebrookova rovnice
Pro turbulentní proudění je nejpřijatelnější rovnicí v měděných a skleněných trubkách rovnice Cyrila Colebrooka (1910-1997), má však tu nevýhodu, že F není to explicitní:
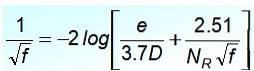
V této rovnici kvocient e / D je relativní drsnost trubky a NR je Reynoldsovo číslo. Pečlivé pozorování ukazuje, že to není snadné nechat F na levou stranu rovnosti, takže není vhodný pro okamžité výpočty.
Colebrook sám navrhl tento přístup, který je explicitní, platný s určitými omezeními:

K čemu to je?
Moodyho diagram je užitečný pro zjištění součinitele tření F zahrnuto v Darcyho rovnici, protože v Colebrookově rovnici není snadné to vyjádřit F přímo z hlediska jiných hodnot.
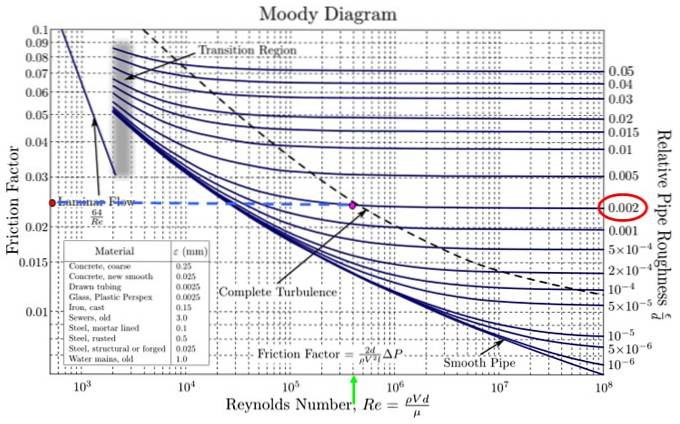
Jeho použití zjednodušuje získání hodnoty F, tím, že obsahuje grafické znázornění F ve funkci NR pro různé hodnoty relativní drsnosti v logaritmickém měřítku.
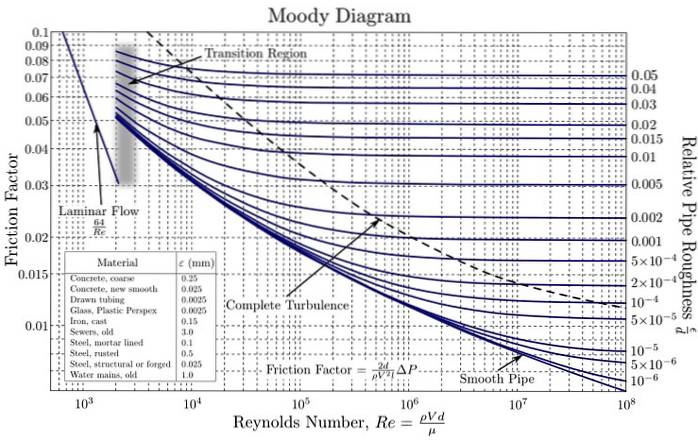
Tyto křivky byly vytvořeny z experimentálních dat s různými materiály běžně používanými při výrobě potrubí. Pomocí logaritmické stupnice pro oba F pokud jde o NR je to nutné, protože pokrývají velmi širokou škálu hodnot. Tímto způsobem je usnadněno vytváření grafů hodnot různých řádů..
První graf Colebrookovy rovnice získal inženýr Hunter Rouse (1906-1996) a krátce poté jej upravil Lewis F. Moody (1880-1953) v podobě, v jaké se používá dodnes..
Používá se pro kruhové i nekruhové trubky, přičemž se za ně jednoduše nahradí hydraulický průměr.
Jak se vyrábí a jak se používá?
Jak bylo vysvětleno výše, Moodyho diagram je vytvořen z mnoha experimentálních dat prezentovaných v grafické podobě. Chcete-li jej použít, postupujte takto:
- Vypočítejte Reynoldsovo číslo NR k určení, zda je tok laminární nebo turbulentní.
- Vypočítejte relativní drsnost pomocí rovnice ar = e / D, kde a je absolutní drsnost materiálu a D je vnitřní průměr trubky. Tyto hodnoty jsou získány prostřednictvím tabulek.
- Teď, když máte ar Y NR, promítněte svisle, dokud nedosáhnete křivky odpovídající ar získané.
- Promítněte vodorovně a doleva a přečtěte hodnotu F.
Příklad pomůže snadno vizualizovat, jak se diagram používá.
-Pracoval příklad 1
Určete třecí faktor pro vodu o teplotě 160 ° F, která teče rychlostí 22 ft / s v potrubí vyrobeném z nepotaženého kovaného železa s vnitřním průměrem 1 palec..
Řešení
Požadovaná data (nalezená v tabulkách):
Kinematická viskozita vody při 160 ° F: 4,38 x 10-6 chodidlodva/ s
Absolutní drsnost nenatřeného tepaného železa: 1,5 x 10 -4 chodidla
První krok
Vypočítá se Reynoldsovo číslo, ale ne dříve, než projdete vnitřním průměrem od 1 palce do stop:
1 palec = 0,0833 stopy
NR = (22 x 0,0833) / 4,38 x 10-6= 4,18 x 10 5
Podle výše uvedených kritérií jde o turbulentní proudění, poté Moodyho diagram umožňuje získat odpovídající třecí faktor, aniž by bylo nutné použít Colebrookovu rovnici.
Druhý krok
Musíte najít relativní drsnost:
ar = 1,5 x 10-4 / 0,0833 = 0,0018
Třetí krok
V dodaném Moodyho diagramu je nutné jít zcela doprava a najít nejbližší relativní drsnost k získané hodnotě. Neexistuje nikdo, kdo odpovídá přesně 0,0018, ale je tu jeden, který je docela blízko, 0,002 (na obrázku červený ovál).
Současně se na vodorovné ose prohledá odpovídající Reynoldsovo číslo. Nejbližší hodnota 4,18 x 10 5 je 4 x 10 5 (zelená šipka na obrázku). Průsečík obou je fuchsiový bod.
Čtvrtý krok
Projděte vlevo po modré tečkované čáře a dosáhněte oranžového bodu. Nyní odhadněte hodnotu F, s přihlédnutím k tomu, že rozdělení nemají stejnou velikost, protože se jedná o logaritmickou stupnici na vodorovné i svislé ose.
Moodyho diagram uvedený na obrázku nemá jemné horizontální dělení, proto hodnota F v 0,024 (je to mezi 0,02 a 0,03, ale není to polovina, ale o něco méně).
Existují online kalkulačky, které používají Colebrookovu rovnici. Jeden z nich (viz odkazy) dodal hodnotu 0,023664639 pro součinitel tření.
Aplikace
Moodyho diagram lze použít k řešení tří typů problémů za předpokladu, že je známa tekutina a absolutní drsnost potrubí:
- Výpočet tlakové ztráty nebo tlakového rozdílu mezi dvěma body za předpokladu délky potrubí, výškového rozdílu mezi dvěma uvažovanými body, rychlosti a vnitřního průměru potrubí.
- Stanovení průtoku, znalost délky a průměru potrubí plus specifická tlaková ztráta.
- Vyhodnocení průměru potrubí, pokud jsou známy délka, průtok a pokles tlaku mezi body, které je třeba vzít v úvahu.
Problémy prvního typu jsou řešeny přímo pomocí diagramu, zatímco problémy druhého a třetího typu vyžadují použití počítačového balíčku. Například u třetího typu, pokud není znám průměr trubky, nelze přímo vyhodnotit Reynoldsovo číslo ani relativní drsnost..
Jedním ze způsobů, jak je vyřešit, je předpokládat počáteční vnitřní průměr a odtud postupně upravovat hodnoty, aby se dosáhlo tlakové ztráty specifikované v problému..
-Pracoval příklad 2
Máte 160 ° F vodu tekoucí rovnoměrně po nepotažené trubce z tepaného železa o průměru 1 palce rychlostí 22 ft / s. Určete tlakový rozdíl způsobený třením a čerpací silou potřebnou k udržení průtoku v délce vodorovné trubky L = 200 stop dlouhé..
Řešení
Potřebná data: gravitační zrychlení je 32 ft / sdva ; měrná hmotnost vody při 160 ° F je γ = 61,0 lb-síla / ft3
Toto je potrubí z vyřešeného příkladu 1, proto je faktor tření již známý F, která byla odhadnuta na 0,0024. Tato hodnota je převzata do Darcyho rovnice pro vyhodnocení ztrát třením:

Požadovaný čerpací výkon je:
W = v. A. (str1 - pdva)
Kde A je plocha průřezu trubice: A = str. (D.dva/ 4) = str. (0,0833dva/ 4) nohadva = 0,00545 stopydva
W = 22 ft / s. 2659,6 lb-síla / ftdva. 0,00545 ftdva= Síla 318,9 lb. chodidla
Výkon se nejlépe vyjadřuje ve wattech, pro které je vyžadován přepočítací faktor:
1 Watt = 0,737 lb-síla. chodidla
Proto je výkon potřebný k udržení průtoku W = 432,7 W
Reference
- Cimbala, C. 2006. Mechanika tekutin, základy a aplikace. Mc. Graw Hill. 335-342.
- Franzini, J. 1999. Fluid Mechanics with Application is in Engineering. Mc. Graw Hill. 176-177.
- LMNO Engineering. Moody Friction Factor Calculator. Obnoveno z: lmnoeng.com.
- Mott, R. 2006. Fluid Mechanics. 4. místo. Edice. Pearson Education. 240-242.
- The Engineering Toolbox. Náladový diagram. Obnoveno z: engineeringtoolbox.com
- Wikipedia. Náladový graf. Obnoveno z: en.wikipedia.org



Zatím žádné komentáře