Rozdíl mezi běžným zlomkem a desetinným číslem

Identifikovat jaký je rozdíl mezi běžným zlomkem a desetinným číslem stačí pozorovat oba prvky: jeden představuje racionální číslo a druhý zahrnuje do své konstrukce celou část a desetinnou část.

„Společný zlomek“ je vyjádření jedné veličiny dělené druhou, aniž by bylo provedeno uvedené dělení. Matematicky je běžným zlomkem racionální číslo, které je definováno jako podíl dvou celých čísel „a / b“, kde b ≠ 0.

„Desetinné číslo“ je číslo, které se skládá ze dvou částí: celočíselné části a desítkové části..

Chcete-li oddělit celočíselnou část od desetinné části, vloží se čárka, která se nazývá desetinná čárka, ačkoli se v závislosti na bibliografii používá také tečka..

Desetinná čísla

Desetinné číslo může mít v desítkové části konečný nebo nekonečný počet čísel. Nekonečný počet desetinných míst lze také rozložit na dva typy:

Periodické

To znamená, že má opakující se vzorec. Například 2.454545454545…

Ne periodické

Nemají žádný opakující se vzor. Například 1.7845265397219…

Čísla, která mají periodické nekonečné nebo nekonečné množství desetinných míst, se nazývají racionální čísla, zatímco ta, která mají neperiodické nekonečné číslo, se nazývají iracionální.

Spojení množiny racionálních čísel a množiny iracionálních čísel je známé jako množina reálných čísel.

Rozdíly mezi běžným zlomkem a desetinným číslem

Rozdíly mezi běžným zlomkem a desetinným číslem jsou:

1 - Desetinná část

Každý běžný zlomek má v desítkové části konečný počet čísel nebo nekonečné periodické číslo, zatímco desítkové číslo může mít v desítkové části nekonečný neperiodický počet čísel..

Výše uvedené říká, že každé racionální číslo (každý běžný zlomek) je desetinné číslo, ale ne každé desetinné číslo je racionální číslo (běžný zlomek).

2- Zápis

Každý společný zlomek je označen jako kvocient dvou celých čísel, zatímco iracionální desetinné číslo nelze tímto způsobem označit..

Nejčastěji používaná iracionální desetinná čísla v matematice jsou označována druhou odmocninou (√ ), kubický (³√ ) a vyšších ročníků.

Kromě nich existují dvě velmi známá čísla, což je Eulerovo číslo, označené e; a číslo pi, označené π.

Jak přejít ze společného zlomku na desetinné číslo?

Chcete-li přejít ze společného zlomku na desetinné číslo, stačí provést odpovídající dělení. Například pokud máte 3/4, odpovídající desetinné číslo je 0,75.

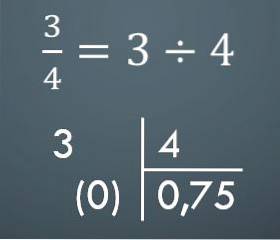
Jak přejít z racionálního desetinného čísla na běžný zlomek?

Lze také provést reverzní proces k předchozímu. Následující příklad ilustruje techniku ​​přechodu z racionálního desetinného čísla na společný zlomek:

- Nechť x = 1,78

Protože x má dvě desetinná místa, předchozí rovnost se vynásobí 10² = 100, čímž získáme 100x = 178; a řešení pro x má za následek, že x = 178/100. Tento poslední výraz je běžný zlomek, který představuje číslo 1,78.

Lze však tento proces provést u čísel s periodickým nekonečným počtem desetinných míst? Odpověď zní ano a následující příklad ukazuje kroky, které je třeba dodržet:

- Nechť x = 2,193193193193…

Protože období tohoto desetinného čísla má 3 číslice (193), předchozí výraz se vynásobí 10³ = 1000, čímž získáme výraz 1000x = 2193.193193193193 ... .

Nyní je poslední výraz odečten od prvního a celá desetinná část je zrušena, takže výraz 999x = 2191, ze kterého získáme, že společný zlomek je x = 2191/999.

Reference

1. Anderson, J. G. (1983). Matematika technického obchodu (Ilustrované vydání.). Industrial Press Inc..
2. Avendaño, J. (1884). Kompletní příručka pro základní a vyšší základní výuku: pro potřeby začínajících učitelů a zejména studentů běžných škol provincie (2. vyd., Sv. 1). Tisk D. Dionisia Hidalga.
3. Coates, G. a. (1833). Argentinská aritmetika: Kompletní pojednání o praktické aritmetice. Pro použití ve školách. Tisk státu.
4. Z moře. (1962). Matematika pro workshop. Reverte.
5. DeVore, R. (2004). Praktické problémy z matematiky pro techniky topení a chlazení (Ilustrované vydání.). Cengage Learning.
6. Jariez, J. (1859). Kompletní kurz fyzikálních a mechanických matematických věd aplikovaných na průmyslové umění (2. vyd.). Železniční tiskárna.
7. Palmer, C. I., & Bibb, S. F. (1979). Praktická matematika: aritmetika, algebra, geometrie, trigonometrie a logaritmické pravítko (dotisk ed.). Reverte.