
Spojité rovnoměrné distribuční charakteristiky, příklady, aplikace
Náhodná proměnná má a kontinuální rovnoměrné rozdělení pokud je pravděpodobnost, že nabere hodnotu, v konečném intervalu [a, b] stejná pro libovolný dílčí interval stejné délky.
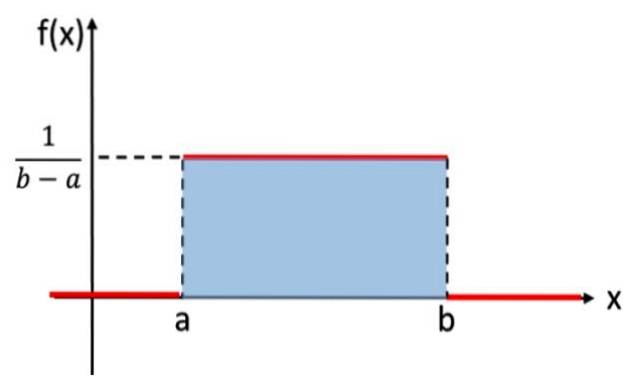
Toto rozdělení je analogické diskrétnímu rovnoměrnému rozdělení, které každému výsledku náhodného experimentu přiřadilo stejnou pravděpodobnost, ale v tomto případě je uvažovaná proměnná spojitá. Například experiment, který spočívá v náhodném výběru reálného čísla mezi hodnotami a a b, sleduje rovnoměrné rozdělení. Zde je jeho graf:
V matematické notaci má spojitá rovnoměrná distribuce funkci hustoty definovanou jako funkci po částech nebo po částech, kterou lze zapsat jako:
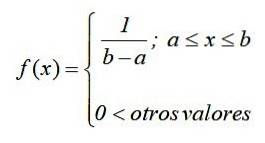
Graf této funkce, známý jako křivka hustoty nebo funkce, je obdélník, proto je spojitá rovnoměrná distribuce známá také jako obdélníkové rozložení y je nejjednodušší ze spojitých distribucí.
Plocha pod grafem rozdělení pravděpodobnosti je rovna 1 a vždy má kladné hodnoty. Jednotná distribuce splňuje tato kritéria. Pro kontrolu, zda je oblast 1, není nutné integrovat přímo, protože plochu stínovaného obdélníku na obrázku 1 lze vypočítat pomocí vzorce:
Plocha = základna x výška = (b - a) x [1 / (b - a)] = 1
Znalost oblasti pod křivkou hustoty je velmi důležitá, protože existuje vztah mezi oblastí a pravděpodobností výskytu události, který je pro toto rozdělení určen v další části.
Charakteristiky spojitého rovnoměrného rozdělení
Kontinuální rovnoměrné rozdělení je charakterizováno jeho:
Funkce hustoty
Nechť X je spojitá náhodná proměnná, která patří do intervalu [a, b], pak:

Distribuční funkce
Distribuční funkce vypočítá pravděpodobnost, že náhodná proměnná X vezme hodnotu x z možných hodnot intervalu [a, b]. Pro spojitou distribuci se obvykle počítá takto:

V případě spojitého rovnoměrného rozdělení se uvedená pravděpodobnost F (x) rovná ploše obdélníku, jehož základna je (x-a) a její výška je (b-a):

Matematicky, pokud F (x) = Pr (X = x), následující funkce je stanovena v částech, podle předchozího výsledku:

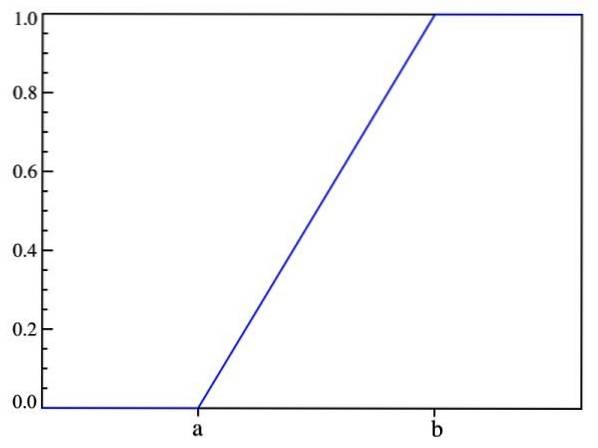
Tímto způsobem se ověřuje to, co bylo řečeno dříve: pravděpodobnost závisí pouze na hodnotě (x-a) a nikoli na jejím umístění v intervalu [a, b]. Graf distribuční funkce je:
Očekávaná hodnota, rozptyl a směrodatná odchylka
Po provedení mnoha experimentů se spojitou náhodnou proměnnou se volá její průměrná hodnota očekávaná hodnota, je označen jako E (X) a je vypočítán následujícím integrálem:

V (X) = E (Xdva) - E (X)dva
Proto:


D (X) = √ V (X)

Medián, režim, symetrie a špičatost
Lze snadno ověřit, že medián, který je centrální hodnotou rovnoměrného rozdělení, se rovná průměru, a protože neexistuje žádná hodnota, která by se opakovala více než ostatní, protože všechny jsou v intervalu [a, b] stejně pravděpodobné , móda neexistuje.
Pokud jde o symetrii, rovnoměrné rozdělení je symetrické a kurtosis, což je míra, do jaké jsou hodnoty soustředěny kolem středu, je -6/5.
Příklady
Průběžnou distribucí lze modelovat různé situace, a tak lze předvídat jejich chování. Zde jsou nějaké příklady:
Příklad 1
Společnost poskytující elektrické služby poskytuje úrovně napětí rovnoměrně rozložené mezi 123,0 V a 125,0 V. To znamená, že v domácí zásuvce je možné získat jakoukoli hodnotu napětí, která patří do tohoto rozsahu..
Jak je vidět výše, grafem funkce hustoty je červený obdélník:

Výpočet pravděpodobnosti napětí v daném intervalu je velmi snadný, například jaká je pravděpodobnost, že společnost pošle napětí nižší než 123,5 V?
Tato pravděpodobnost se rovná oblasti obdélníku stínované modře:
P (X<123.5) = (123.5 −123.0)x 0.5 = 0.25
A jaká je pravděpodobnost, že dodané napětí je větší než 124,0 V?
Jelikož se celková plocha rovná 1, hledaná pravděpodobnost je:
P (X> 124,0 V) = 1 - (1 × 0,5) = 0,5
Dává to smysl, protože 124.0 je přesně hodnota ve středu intervalu.
Příklad 2
Určitá náhodná proměnná X má rovnoměrné rozdělení v intervalu [0,100]. Rozhodni se:
a) Pravděpodobnost, že hodnota X je menší než 22.
b) Pravděpodobnost, že X nabude hodnot mezi 20 a 35.
c) Očekávaná hodnota, rozptyl a směrodatná odchylka tohoto rozdělení.
Odpovědět
Je určen podobným způsobem jako v předchozím příkladu, ale nejprve musíme určit výšku obdélníku, pamatujeme si, že celková plocha musí být rovna 1:
Plocha = 100 × výška = 1
Proto má obdélník výšku rovnou 1/100 = 0,01
P (X<22) = 22×0.01 = 0.22
Odpověď b
Požadovaná pravděpodobnost se rovná ploše obdélníku, jehož šířka je (35 - 20) a jehož výška je 0,01:
P (22 Pokud dáváte přednost přímému přechodu na distribuční funkci uvedenou výše, stačí nahradit hodnoty v: P (20≤X≤35) = F (35) -F (20) S F (x) dané: F (x) = (x-a) / (b-a) Hodnoty, které je třeba zadat, jsou: a = 0 b = 100 F (35) = (35-0) / (100-0) = 0,35 F (20) = (20-0) / (100-0) = 0,20 P (20≤X≤35) = 0,35-0,20 = 0,15 Očekávaná hodnota je: E (X) = (a + b) / 2 = (100 + 0) / 2 = 50 Rozptyl je: V (X) = (b-a)dva/ 12 = (100-0)dva/ 12 = 833,33 A standardní odchylka je: D (X) = √ 833,33 = 28,87 Toto rozdělení je užitečné při provádění statistických simulačních procesů nebo při práci na událostech, jejichž četnost výskytu je pravidelná.. Některé programovací jazyky generují náhodná čísla mezi 0 a 1 a jak je patrné z předchozích příkladů, sledované rozdělení pravděpodobnosti je jednotné. V tomto případě je uvažovaný interval [0,1]. Pokud máte experiment, ve kterém mají události pravidelnost, jak bylo vysvětleno výše, můžete v zásadě každému z nich přiřadit stejnou pravděpodobnost výskytu. V tomto případě poskytuje pravděpodobnostní model rovnoměrného rozdělení informace pro analýzu.. Rovnoměrné rozdělení se také používá při zaokrouhlování rozdílů mezi pozorovanými hodnotami a skutečnými hodnotami proměnné, za předpokladu rovnoměrného rozložení chyby v daném intervalu, podle zaokrouhlování, obvykle od -0,5 do +0,5.Odpověď c
Aplikace
Generování náhodných čísel
Vzorkování libovolných distribucí
Zaokrouhlování chyb
Reference



Zatím žádné komentáře