
Charakteristiky diskrétního rozdělení pravděpodobnosti, cvičení
The diskrétní rozdělení pravděpodobnosti jsou funkcí, která přiřadí každému prvku X (S) = x1, x2,…, xi,…, kde X je daná diskrétní náhodná proměnná a S je její ukázkový prostor, pravděpodobnost, že k dané události dojde. Tato funkce f z X (S) definovaná jako f (xi) = P (X = xi) se někdy nazývá funkce pravděpodobnostní hmotnosti.
Tato hmotnost pravděpodobností je obecně reprezentována ve formě tabulky. Protože X je diskrétní náhodná proměnná, X (S) má konečný počet událostí nebo spočítatelné nekonečno. Mezi nejběžnější diskrétní rozdělení pravděpodobnosti patří rovnoměrné rozdělení, binomické rozdělení a Poissonovo rozdělení.
Rejstřík článků
- 1 Funkce
- 2 druhy
- 2.1 Rovnoměrné rozdělení přes n bodů
- 2.2 Binomické rozdělení
- 2.3 Poissonovo rozdělení
- 2.4 Hypergeometrická distribuce
- 3 Vyřešená cvičení
- 3.1 První cvičení
- 3.2 Druhé cvičení
- 3.3 Třetí cvičení
- 3.4 Třetí cvičení
- 4 Odkazy
Vlastnosti
Funkce rozdělení pravděpodobnosti musí splňovat následující podmínky:
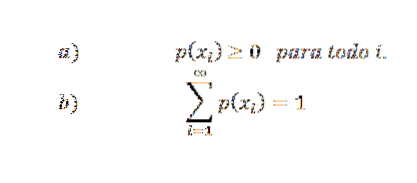
Dále, pokud X vezme pouze konečný počet hodnot (například x1, x2,…, xn), pak p (xi) = 0, pokud i> ny, tedy nekonečná řada podmínky b se stane konečnou řadou.
Tato funkce také splňuje následující vlastnosti:
Nechť B je událost spojená s náhodnou proměnnou X. To znamená, že B je obsažena v X (S). Konkrétně předpokládejme, že B = xi1, xi2,…. Proto:
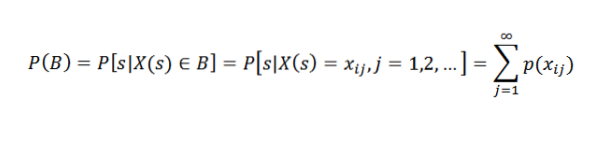
Jinými slovy: pravděpodobnost události B se rovná součtu pravděpodobností jednotlivých výsledků spojených s B.
Z toho můžeme usoudit, že pokud a < b, los sucesos (X ≤ a) y (a < X ≤ b) son mutuamente excluyentes y, además, su unión es el suceso (X ≤ b), por lo que tenemos:
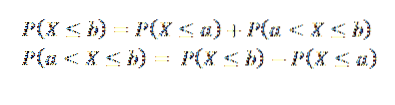
Typy
Rovnoměrné rozdělení přes n bodů
O náhodné proměnné X se říká, že sleduje distribuci charakterizovanou jednotností v n bodech, pokud je každé hodnotě přiřazena stejná pravděpodobnost. Jeho funkce pravděpodobnostní hmotnosti je:
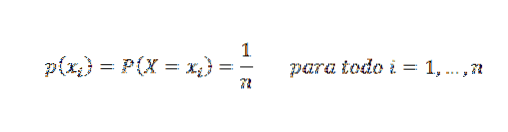
Předpokládejme, že máme experiment, který má dva možné výsledky, může to být hod mincí, jehož možnými výsledky jsou hlavy nebo ocasy, nebo volba celého čísla, jehož výsledkem může být sudé číslo nebo lichý; tento typ experimentu je znám jako Bernoulliho testy.
Obecně se dvěma možným výsledkům říká úspěch a neúspěch, kde p je pravděpodobnost úspěchu a 1-p je pravděpodobnost neúspěchu. Můžeme určit pravděpodobnost x úspěchů v n Bernoulliho testech, které jsou na sobě nezávislé, s následující distribucí.
Binomická distribuce
Je to funkce, která představuje pravděpodobnost získání x úspěchů v n nezávislých Bernoulliho testech, jejichž pravděpodobnost úspěchu je p. Jeho funkce pravděpodobnostní hmotnosti je:
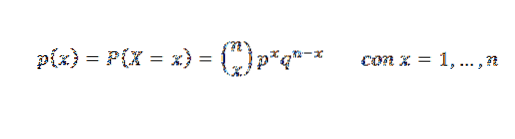
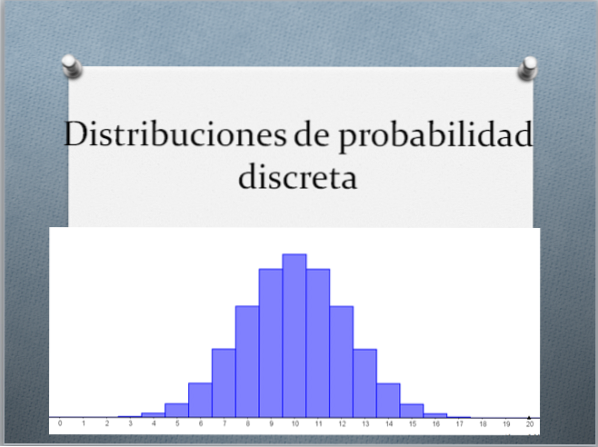
Následující graf představuje funkci pravděpodobnostní hmotnosti pro různé hodnoty parametrů binomického rozdělení.
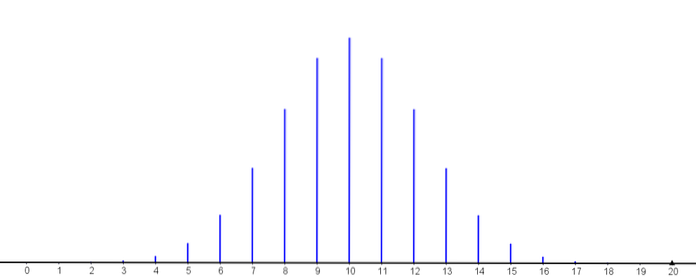
Následující distribuce vděčí za své jméno francouzskému matematikovi Simeonovi Poissonovi (1781-1840), který jej získal jako limit binomického rozdělení.
Poissonovo rozdělení
O náhodné proměnné X se říká, že má Poissonovo rozdělení parametru λ, když může nabývat kladných celočíselných hodnot 0,1,2,3, ... s následující pravděpodobností:
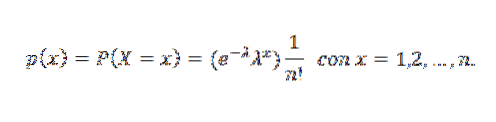
V tomto výrazu λ je průměrný počet odpovídající výskytům události pro každou jednotku času a x je počet výskytů události.
Jeho funkce pravděpodobnostní hmotnosti je:
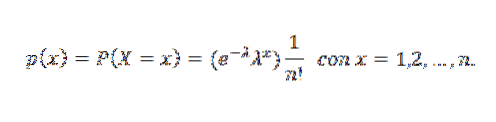
Dále graf, který představuje funkci pravděpodobnostní hmotnosti pro různé hodnoty parametrů Poissonova rozdělení.
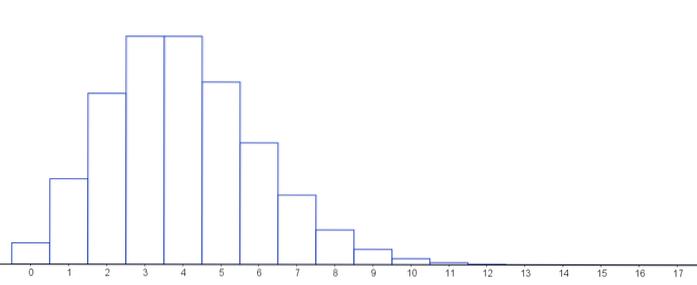
Všimněte si, že pokud je počet úspěchů nízký a počet testů prováděných na binomické distribuci vysoký, můžeme tyto distribuce vždy přiblížit, protože Poissonovo rozdělení je limitem binomického rozdělení.
Hlavní rozdíl mezi těmito dvěma distribucemi spočívá v tom, že zatímco dvojčlen závisí na dvou parametrech - jmenovitě n a p-, Poisson závisí pouze na λ, kterému se někdy říká intenzita distribuce..
Zatím jsme mluvili pouze o rozdělení pravděpodobnosti pro případy, kdy jsou různé experimenty na sobě nezávislé; to znamená, když výsledek jednoho není ovlivněn jiným výsledkem.
V případě experimentů, které nejsou nezávislé, je hypergeometrická distribuce velmi užitečná.
Hypergeometrická distribuce
Nechť N je celkový počet objektů konečné množiny, z nichž můžeme nějakým způsobem identifikovat k, čímž vytvoříme podmnožinu K, jejíž komplement je tvořen zbývajícími N-k prvky.
Pokud náhodně vybereme n objektů, náhodná proměnná X, která představuje počet objektů náležejících ke K v dané volbě, má hypergeometrické rozdělení parametrů N, na ak. Jeho funkce pravděpodobnostní hmotnosti je:
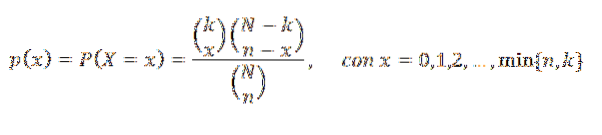
Následující graf představuje funkci pravděpodobnostní hmotnosti pro různé hodnoty parametrů hypergeometrického rozdělení.
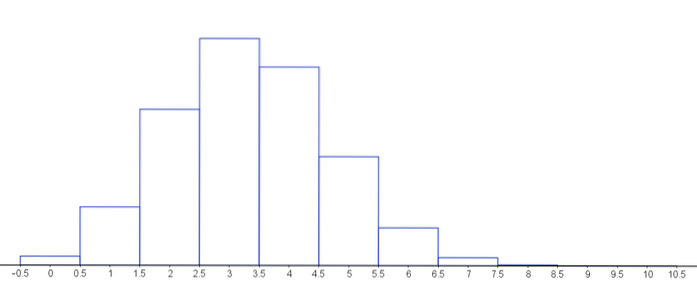
Vyřešená cvičení
První cvičení
Předpokládejme, že pravděpodobnost, že rádiová trubice (umístěná v určitém typu zařízení) bude fungovat déle než 500 hodin, je 0,2. Pokud je testováno 20 zkumavek, jaká je pravděpodobnost, že přesně k z nich bude fungovat déle než 500 hodin, k = 0, 1,2,…, 20?
Řešení
Pokud X je počet zkumavek, které pracují více než 500 hodin, předpokládáme, že X má binomické rozdělení. Pak
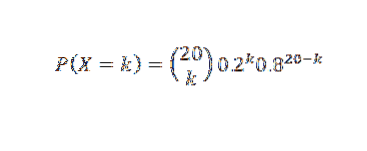
A tak:

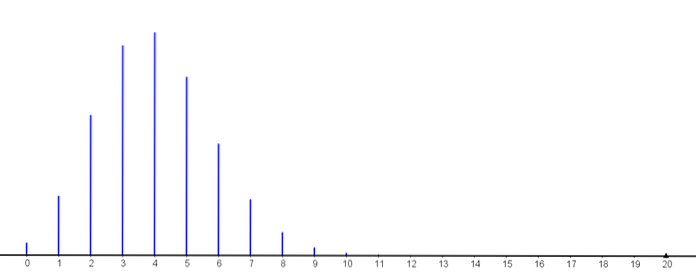
Pro k≥11 jsou pravděpodobnosti menší než 0,001
Můžeme tedy pozorovat, jak se zvyšuje pravděpodobnost, že k z nich bude fungovat déle než 500 hodin, dokud nedosáhne své maximální hodnoty (s k = 4) a poté začne klesat..
Druhé cvičení
Mince je hodena 6krát. Když je výsledek drahý, řekneme, že je to úspěch. Jaká je pravděpodobnost, že dvě hlavy přijdou přesně?
Řešení
V tomto případě máme n = 6 a pravděpodobnost úspěchu i neúspěchu je p = q = 1/2
Proto je pravděpodobnost, že budou dány dvě hlavy (tj. K = 2)
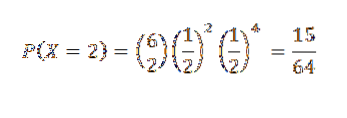
Třetí cvičení
Jaká je pravděpodobnost nalezení alespoň čtyř hlav?
Řešení
V tomto případě máme k = 4, 5 nebo 6
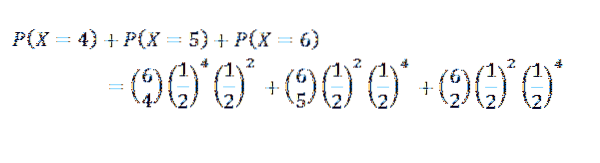
Třetí cvičení
Předpokládejme, že 2% položek vyrobených v továrně je vadných. Zjistěte pravděpodobnost P, že ve vzorku 100 položek jsou tři vadné položky.
Řešení
V tomto případě bychom mohli použít binomické rozdělení pro n = 100 ap = 0,02, což by mělo být výsledkem:
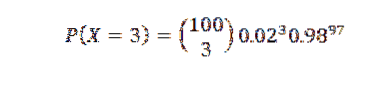
Protože však p je malé, použijeme Poissonovu aproximaci s λ = np = 2. A) Ano,
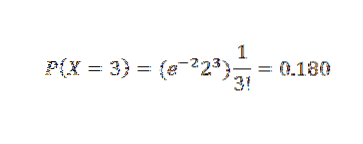
Reference
- Kai Lai Chung. Teorie základní stability se stochastickými procesy. Springer-Verlag New York Inc.
- Kenneth.H. Rosen. Diskrétní matematika a její aplikace. S.A. MCGRAW-HILL / INTERAMERICANA DE ESPAÑA.
- Paul L. Meyer. Pravděpodobnost a statistické aplikace. S.A. MEXICKÁ ALHAMBRA.
- Seymour Lipschutz Ph.D. 2000 Vyřešené problémy diskrétní matematiky. McGRAW-HILL.
- Seymour Lipschutz Ph.D. Teorie a pravděpodobnostní problémy. McGRAW-HILL.



Zatím žádné komentáře