Vzorec rovnic prvního stupně, jak je řešit, příklad, cvičení

The první stupeň nebo lineární rovnice s neznámým jsou ty, které lze vyjádřit jako součet dvou členů, a to následovně:

ax + b = 0

Kde a a b, s na ≠ 0, jsou reálná čísla R nebo také komplexní C. Abychom to vyřešili, termíny jsou transponovány, což znamená změnu termínů z jedné strany rovnosti na druhou.

Abychom vyřešili neznámé, je transponován termín + b, který musí jít na pravou stranu rovnosti se změněným znaménkem.

ax = -b

Pak je hodnota x vymazána, například takto:

x = - b / a

Jako příklad budeme řešit následující rovnici:

6x - 5 = 4

Transponujeme termín -5 na pravou stranu se změněným znaménkem:

6x = 4 + 5

To odpovídá přidání 5 na obě strany původní rovnice:

6x - 5 + 5 = 4 + 5 → 6x = 9

A teď vyřešíme neznámé „x“:

x = 9/6 = 3/2

Což odpovídá rozdělení obou stran rovnosti na 6. Takže k získání řešení můžeme použít následující:

-Stejné množství lze přidat nebo odečíst z obou stran rovnosti v rovnici, aniž byste ji změnili.

-Rovněž můžete vynásobit (nebo rozdělit) stejnou částkou všechny výrazy nalevo i napravo od rovnice.

-A pokud jsou oba členové rovnice povýšeni na stejnou moc, rovnost se také nezmění.

Rejstřík článků

• 1 Jak řešit rovnice prvního stupně
  • 1.1 Grafická interpretace
• 2 Příklady jednoduchých lineárních rovnic   
  • 2.1 Celočíselné rovnice
  • 2.2 Frakční rovnice
  • 2.3 Doslovné rovnice
  • 2.4 Systémy rovnic prvního stupně 
  • 2.5 Lineární rovnice s absolutní hodnotou
• 3 jednoduchá řešená cvičení
  • 3.1 - Cvičení 1
  • 3.2 - Cvičení 2
  • 3.3 - Cvičení 3
• 4 Odkazy

Jak řešit rovnice prvního stupně

Řešení rovnice prvního stupně je také známé jako její kořen. Je to hodnota x, která převádí původní výraz na rovnost. Například v:

5x = 8x - 15

Pokud v této rovnici dosadíme x = 5, dostaneme:

5⋅5 = 8⋅5 - 15

25 = 40 - 15

25 = 25

Protože lineární rovnice prvního stupně přicházejí v mnoha formách, které někdy nejsou zřejmé, existuje řada obecných pravidel, která zahrnují různé algebraické manipulace, aby se zjistila hodnota neznáma:

-Nejprve, pokud jsou indikovány operace, měly by být provedeny.

-Seskupování symbolů, jako jsou závorky, hranaté závorky a složené závorky, pokud existují, by měly být odstraněny, aby byly zachovány příslušné znaky.

-Podmínky jsou transponovány tak, aby byly všechny, které obsahují neznámé, umístěny na jednu stranu rovnosti a ty, které ji neobsahují, na druhou stranu.

-Potom se všechny podobné výrazy zredukují, aby se dospělo k formuláři ax = -b.

-A posledním krokem je vyčistit neznámo.

Grafická interpretace

Rovnici prvního stupně zvednutou na začátku lze odvodit z rovnice přímky y = mx + c, takže y = 0. Výsledná hodnota x odpovídá průsečíku přímky s vodorovnou osou.

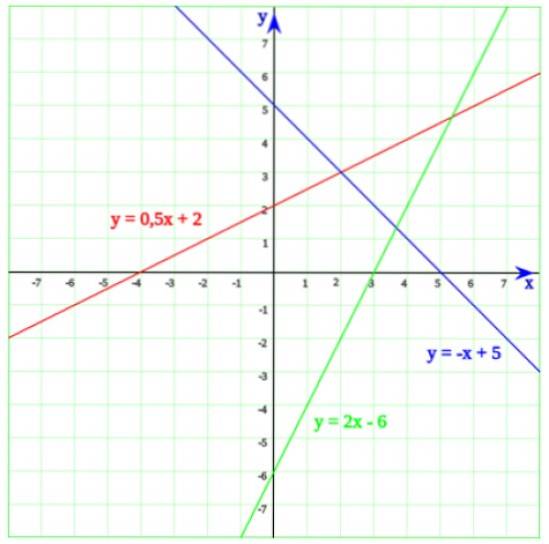
Na následujícím obrázku jsou tři řádky. Počínaje zelenou čarou, jejíž rovnice je:

y = 2x - 6

Z y = 0 v rovnici přímky se získá rovnice prvního stupně:

2x - 6 = 0

Čí řešení je x = 6/2 = 3. Nyní, když podrobně popisujeme graf, je snadné si uvědomit, že ve skutečnosti čára protíná vodorovnou osu v x = 3.

Modrá čára protíná osu x na x = 5, což je řešení rovnice -x + 5 = 0. Nakonec čára, jejíž rovnice je y = 0,5x + 2, protíná osu x na x = - 4 , což je snadno patrné z rovnice prvního stupně:

0,5 x + 2 = 0

x = 2 / 0,5 = 4

Příklady jednoduchých lineárních rovnic   

Celočíselné rovnice

Jsou to ti, v jejichž podmínkách neexistují žádní jmenovatelé, například:

21 - 6x = 27 - 8x

Vaše řešení je:

-6x + 8x = 27 - 21

2x = 6

x = 3

Frakční rovnice

Tyto rovnice obsahují alespoň jeden jmenovatel jiný než 1. Abychom je vyřešili, je vhodné znásobit všechny termíny nejmenším společným násobkem (LCM) jmenovatelů, abychom je vyloučili.

Následující rovnice je zlomkového typu:

Protože jsou tato čísla malá, není těžké vidět, že m.c.m (6, 8,12) = 24. Tento výsledek lze snadno získat vyjádřením čísel jako součin prvočísel nebo jejich mocnin, pojďme se podívat:

6 = 3,2

8 = 2³

12 = 2^dva⋅3

Nejmenší společný násobek je určen vynásobením běžných a neobvyklých faktorů 6, 8 a 12 jejich největším exponentem, poté:

lcm (6,8,12) = 2³ ⋅3 = 8 × 3 = 24

Protože máme nejméně společný násobek, musí se vynásobit každým z výrazů rovnice:

4 (x + 5) -3 (2x + 3) = 2 (1-5x)

Využíváme distribuční majetek:

4x + 20 - 6x -9 = 2 - 10x

Všechny výrazy, které obsahují neznámé „x“, jsou seskupeny na levé straně rovnosti a nezávislé nebo číselné výrazy jsou ponechány na pravé straně:

4x - 6x + 10 x = 2 +9 - 20

8x = -9

x = - 9/8

Doslovné rovnice

Jsou to lineární rovnice s jednou neznámou, které jsou však doprovázeny doslovnými koeficienty (písmeny). S těmito písmeny se zachází stejně jako s čísly. Příklad doslovné rovnice prvního stupně je:

-3ax + 2a = 5x - b

Tato rovnice je řešena stejným způsobem, jako kdyby byly nezávislé členy a koeficienty číselné:

-3ax - 5x = - b - 2a

Faktorování neznámého „x“:

x (-3a - 5) = - b - 2a

x = (- b - 2a) / (-3a - 5) → x = (2a + b) / (3a + 5)

Soustavy rovnic prvního stupně 

Systémy rovnic se skládají ze sady rovnic se dvěma nebo více neznámými. Řešení systému se skládá z hodnot, které splňují rovnice současně a pro jeho jednoznačné určení musí existovat rovnice pro každou neznámou.

Obecná forma systému m lineární rovnice s n neznámé je:

na_jedenáctX₁ + na₁₂X_dva +… Do_1nX_n = b₁
na_{dvacet jedna}X₁ + na₂₂X_dva +… Do_2nX_n = b_dva
...
na_m1X₁ + na_m2X_dva +… Do_mnX_n = b_m

Pokud má systém řešení, říká se, že je kompatibilní stanoveno, když existuje nekonečná sada hodnot, které ji uspokojují neurčitý kompatibilní, a konečně, pokud nemá řešení, pak je nekompatibilní.

Při řešení systémů lineárních rovnic se používá několik metod: redukce, substituce, ekvalizace, grafické metody, Gauss-Jordanova eliminace a použití determinantů. K dosažení řešení však existují další algoritmy, které jsou výhodnější pro systémy s mnoha rovnicemi a neznámými.

Příkladem soustavy lineárních rovnic se dvěma neznámými je:

8x - 5 = 7y - 9
6x = 3y + 6

Řešení tohoto systému je představeno dále v sekci řešených cvičení..

Lineární rovnice s absolutní hodnotou

Absolutní hodnota reálného čísla je vzdálenost mezi jeho umístěním na číselném řádku a 0 na číselném řádku. Jelikož se jedná o vzdálenost, její hodnota je vždy kladná.

Absolutní hodnota čísla je označena modulo pruhy: │x│. Absolutní hodnota kladného nebo záporného čísla je vždy kladná, například:

│ + 8│ = 8

│-3│ = 3

V rovnici absolutní hodnoty je neznámo mezi pruhy modulu. Zvažme následující jednoduchou rovnici:

│x│ = 10

Existují dvě možnosti, první je, že x je kladné číslo, v takovém případě máme:

x = 10

Další možností je, že x je záporné číslo, v tomto případě:

x = -10

Toto jsou řešení této rovnice. Nyní se podívejme na jiný příklad:

│x + 6│ = 11

Množství uvnitř pruhů může být kladné, takže:

x + 6 = 11

x = 11 -6 = 5

Nebo to může být negativní. V tom případě:

-(x + 6) = 11

-x - 6 = 11 ⇒ -x = 11 + 6 = 17

A hodnota neznámého je:

x = -17

Tato rovnice absolutní hodnoty má tedy dvě řešení: x₁ = 5 a x_dva = -17. Můžeme zkontrolovat, že obě řešení vedou k rovnosti v původní rovnici:

│5 + 6│ = 11

│11│ = 11

Y

│-17 + 6│ = 11

│-11│ = 11

Jednoduchá řešená cvičení

- Cvičení 1

Vyřešte následující systém lineárních rovnic dvěma neznámými:

8x - 5 = 7y -9
6x = 3y + 6

Řešení

Jak je navrženo, tento systém je ideální pro použití substituční metody, protože ve druhé rovnici neznámo X je téměř připraven k odbavení:

x = (3y + 6) / 6

Může být okamžitě nahrazen první rovnicí, která se poté stane rovnicí prvního stupně s neznámým „y“:

8 [(3r + 6) / 6] - 5 = 7r - 9

Jmenovatel lze odstranit vynásobením každého výrazu číslem 6:

6. 8⋅ [(3y + 6) / 6] - 6,5 = 6,7y- 6. 9

8⋅ (3r + 6) - 30 = 42r - 54

Uplatnění distribuční vlastnosti v prvním termínu vpravo od rovnosti:

24y + 48 -30 = 42y - 54 ⇒ 24y + 18 = 42y - 54

Rovnici lze zjednodušit, protože všechny koeficienty jsou násobky 6:

4y + 3 = 7y - 9

-3y = -12

y = 4

S tímto výsledkem přejdeme na clearing x:

x = (3y +6) / 6 → x = (12 + 6) / 6 = 3

- Cvičení 2

Vyřešte následující rovnici:

Řešení

Produkty se objevují v této rovnici a podle pokynů uvedených na začátku je nejprve nutné vyvinout:

3x - 10x +14 = 5x + 36x + 12

Pak jsou všechny výrazy, které obsahují neznámé, přeneseny na levou stranu rovnosti a na pravou stranu budou nezávislé výrazy:

3x - 10x - 5x - 36x = 12 - 14

-48x = -2

x = 1/24

- Cvičení 3

Přidáním tří vnitřních úhlů trojúhelníku získáte 180 °. Major převyšuje menší o 35 ° a druhý zase převyšuje o 20 ° rozdíl mezi majorem a médiem. Jaké jsou úhly?

Řešení

Nazveme „x“ větší úhel, „y“ prostřední a „z“ nejmenší. Když prohlášení potvrdí, že jejich součet je 180 °, lze napsat:

x + y + z = 180

Pak víme, že čím větší převyšuje menší o 35 °, můžeme to napsat takto:

x = z + 35

A konečně nejmenší přesahuje rozdíl mezi největším a středním o 20 °:

z = x - y + 20

Máme systém 3 rovnic a 3 neznámých:

x + y + z = 180

x = z + 35

z = x - y + 20

Řešení pro z z první rovnice máme:

z = 180 - x - y

Shoda s třetím:

180 - x - y = x - y + 20

Předávání neznámých na levou stranu jako vždy:

-x - y - x + y = 20 - 180

Písmeno „y“ je zrušeno a zůstává:

-2x = - 160

x = 80 °

Z druhé rovnice zjistíme hodnotu z:

z = x - 35 = 80 - 35 = 45 °

A hodnota y se nachází od první nebo třetí:

y = 180 - x - z = 180 - 80 - 45 = 55 °

Reference

1. Baldor. 1977. Elementární algebra. Venezuelské kulturní edice.
2. Montereyův institut. Rovnice, nerovnice a absolutní hodnota. Obnoveno z: montereyinstitute.org.
3. Online učitel. Klasifikace lineárních rovnic nebo rovnic prvního stupně. Obnoveno z: profesorenlinea.cl.
4. Hoffman, J. Výběr témat matematiky. Svazek 2.
5. Jiménez, R. 2008. Algebra. Hala Prentice.
6. Zill, D. 1984. Algebra a trigonometrie. Mcgraw kopec.