
Eneagon vlastnosti, jak udělat eneagon, příklady

A eneagon je mnohoúhelník s devíti stranami a devíti vrcholy, které mohou nebo nemusí být pravidelné. Jméno eneágono pochází z řečtiny a je tvořeno řeckými slovy ennea (devět a gonon (úhel).
Alternativní název pro devítiboký polygon je nonagon, slovo, které pochází z latiny nonus (devět a gonon (vrchol). Na druhou stranu, pokud jsou strany nebo úhly enegonu navzájem nerovné, pak máme a nepravidelný enegon. Pokud je naopak devět stran a devět úhlů enegonu stejných, pak je to a pravidelný enegon.
Rejstřík článků
- 1 Vlastnosti enegonu
- 1.1 Pravidelný enegon
- 1.2 Oblast enegonu známá strana a apothem
- 1.3 Oblast známého enegonu na boku
- 1.4 Obvod pravidelného enegonu znal jeho stranu
- 1,5 Obvod enegonu zná jeho poloměr
- 2 Jak vyrobit pravidelný eneagon
- 3 příklady
- 3.1 Příklad 1
- 3.2 Příklad 2
- 4 Odkazy
Vlastnosti Eneagonu
Pro mnohoúhelník s n stranami je součet jeho vnitřních úhlů:
(n - 2) * 180 °
V enegonu by to bylo n = 9, takže součet jeho vnitřních úhlů je:
Sa = (9 - 2) * 180 ° = 7 * 180 ° = 1260 °
V libovolném mnohoúhelníku je počet úhlopříček:
D = n (n - 3) / 2 a v případě enegonu, protože n = 9, máme potom D = 27.
Pravidelný enegon
V pravidelném eneagonu nebo nonagonu je devět (9) vnitřních úhlů stejné míry, proto každý úhel měří jednu devátinu z celkového součtu vnitřních úhlů.
Míra vnitřních úhlů enegonu je pak 1260 ° / 9 = 140 °.
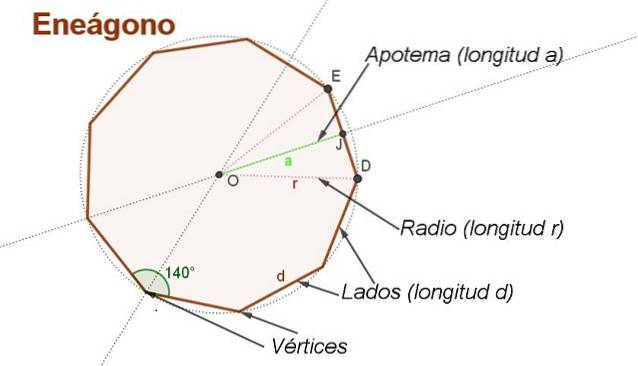
Odvodit vzorec pro oblast regulárního enegonu s side d je vhodné vyrobit některé pomocné konstrukce, jako jsou ty, které jsou znázorněny na obrázku 2.
Centrum se nachází NEBO sledování půlek dvou sousedních stran. Střed NEBO ve stejné vzdálenosti od vrcholů.
Poloměr délky r je segment, který jde od středu NEBO k vrcholu enegonu. Poloměry jsou znázorněny na obrázku 2. OD Y OE délky r.
Apothem je segment, který jde od středu ke středu jedné strany enegonu. Například Úř. Věst je apothem, jehož délka je na.
Oblast známého enegonu na boku a apotému
Zvažujeme trojúhelník ÓDA obrázku 2. Plocha tohoto trojúhelníku je součinem jeho základny Z pro výšku Úř. Věst děleno 2:
Plocha ÓDA = (DE * Úř. Věst.) / 2 = (d * a) / 2
Vzhledem k tomu, že v enegonu je 9 trojúhelníků stejné oblasti, došlo se k závěru, že stejná oblast je:
Eneagonská oblast = (9/2) (d * a)
Oblast známého enegonu na boku
Pokud je známa pouze délka d stran enegonu, je nutné zjistit délku apothemu, aby bylo možné použít vzorec z předchozí části.
Zvažujeme trojúhelník OKO obdélník dovnitř J (viz obrázek 2). Pokud se použije tangenciální trigonometrický poměr, získáme:
tak(∡OEJ) = Úř. Věst / Př.
Úhel ∡OEJ = 140º / 2 = 70º EO půlící úhel vnitřního úhlu enegonu.
Na druhou stranu, Úř. Věst je apotém délky na.
Pak jako J je středem ED z toho vyplývá, že EJ = d / 2.
Dosazením předchozích hodnot v tangenciálním vztahu máme:
opálení (70 °) = a / (d / 2).
Nyní vyčistíme délku apothemu:
a = (d / 2) opálení (70 °).
Předchozí výsledek se ve vzorci oblasti nahradí a získá se:
Eneagonská oblast = (9/2) (d * a) = (9/2)( d * (d / 2) opálení (70 °))
Nakonec najdeme vzorec, který umožňuje získat plochu regulárního enegonu, pokud je známa pouze jeho délka d z jeho stran:
Eneagonská oblast = (9/4) ddva opálení (70 °) = 6,1818 ddva
Obvod pravidelného enegonu znal jeho stranu
Obvod mnohoúhelníku je součtem jeho stran. V případě enegonu, protože každá ze stran měří délku d, jeho obvod bude součet devítinásobku d, a to:
Obvod = 9 d
Obvod enegonu znal jeho poloměr
Vzhledem k trojúhelníku OKO obdélník dovnitř J (viz obrázek 2), použije se trigonometrický kosinový poměr:
cos (∡OEJ) = Př / OE = (d / 2) / r
Odkud se získává:
d = 2r cos (70 °)
Dosazením tohoto výsledku získáme vzorec pro obvod jako funkci poloměru enegonu:
Obvod = 9 d = 18 r cos (70 °) = 6,1564 r
Jak udělat pravidelný eneagon
1 - Chcete-li postavit pravidelného eneagona s pravítkem a kompasem, začněte od obvodu C který vymezuje enegon. (viz obrázek 3)
2 - Středem O obvodu jsou nakresleny dvě kolmé čáry. Poté jsou průsečíky A a B jedné z čar označeny obvodem.
3- S kompasem, centrovaným na průsečíku B a otvorem rovným poloměru BO, se nakreslí oblouk, který protne původní obvod v bodě C.
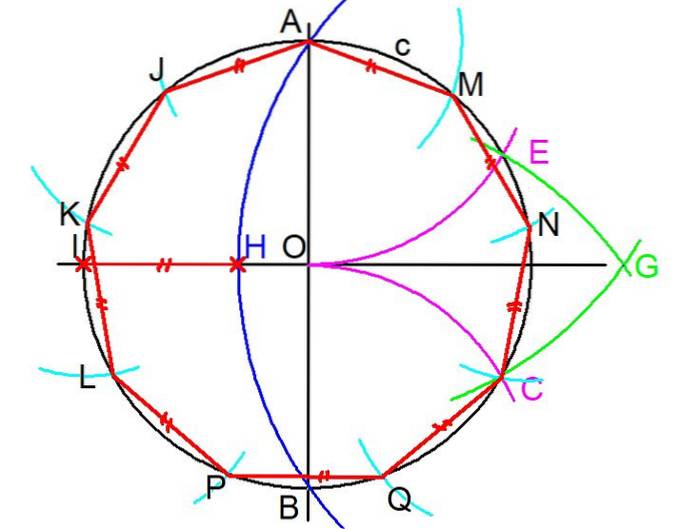
4- Předchozí krok se opakuje, ale při vytvoření středu v A a poloměru AO se nakreslí oblouk, který protne obvod c v bodě E.
5- S otevřením AC a středem v A se nakreslí oblouk obvodu. Podobně s otevřením BE a středem B je nakreslen další oblouk. Průsečík těchto dvou oblouků je označen jako bod G.
6- Centrování v G a otevření GA, nakreslí se oblouk, který protíná sekundární osu (v tomto případě horizontální) v bodě H. Průsečík sekundární osy s původním obvodem c je označen jako I.
7- Délka segmentu IH se rovná délce d strany enegonu.
8- Při otevření kompasu IH = d se postupně vykreslí oblouky poloměru středu A, poloměru J, středu AK, poloměru K, středu KL a poloměru L, LP.
9- Podobně počínaje A a z pravé strany jsou nakresleny oblouky o poloměru IH = d, které označují body M, N, C a Q na původním obvodu c.
10- Nakonec jsou nakresleny segmenty AJ, JK, KL, LP, AM, MN, NC, CQ a nakonec PB.
Je třeba poznamenat, že konstrukční metoda není zcela přesná, protože lze ověřit, že poslední strana PB je o 0,7% delší než ostatní strany. K dnešnímu dni není známa žádná metoda konstrukce s pravítkem a kompasem, která by byla 100% přesná..
Příklady
Zde je několik zpracovaných příkladů.
Příklad 1
Chcete vytvořit pravidelný enegon, jehož strany měří 2 cm. Jaký poloměr musí mít obvod, který jej obklopuje, aby se při použití výše popsané konstrukce dosáhlo požadovaného výsledku?
Řešení:
V předchozí části byl odvozen vzorec, který souvisí s poloměrem r popsané kružnice se stranou d pravidelného enegonu:
d = 2r cos (70 °)
Řešení pro r z předchozího výrazu máme:
r = d / (2 cos (70 °)) = 1,4619 * d
Dosazením hodnoty d = 2 cm v předchozím vzorci se získá poloměr r 2,92 cm.
Příklad 2
Jaká je plocha pravidelného enegonu se stranou 2 cm?
Řešení:
Abychom mohli odpovědět na tuto otázku, musíme se odvolat na výše zobrazený vzorec, který nám umožňuje najít oblast známého enegonu podle délky d jeho strany:
Eneagonská oblast = (9/4) ddva opálení (70 °) = 6,1818 ddva
Dosazením d za jeho hodnotu 2 cm v předchozím vzorci získáme:
Eneagonská oblast = 24,72 cm
Reference
- C. E. A. (2003). Prvky geometrie: s cvičeními a geometrií kompasu. University of Medellin.
- Campos, F., Cerecedo, F. J. (2014). Matematika 2. Grupo Redakční Patria.
- Freed, K. (2007). Objevte mnohoúhelníky. Benchmark Education Company.
- Hendrik, V. (2013). Zobecněné polygony. Birkhäuser.
- IGER. (s.f.). Matematika v prvním semestru Tacaná. IGER.
- Jr. geometrie. (2014). Mnohoúhelníky. Lulu Press, Inc..
- Miller, Heeren a Hornsby. (2006). Mathematics: Reasoning And Applications (desáté vydání). Pearson Education.
- Patiño, M. (2006). Matematika 5. Redakční program.



Zatím žádné komentáře