
Gravitační energetické vzorce, charakteristiky, aplikace, cvičení
The gravitační energie Je to ten, který má masivní objekt, když je ponořen do gravitačního pole vytvářeného jiným. Některé příklady objektů s gravitační energií jsou: jablko ve stromu, padající jablko, Měsíc obíhající kolem Země a Země obíhající kolem Slunce.
Isaac Newton (1642-1727) si jako první uvědomil, že gravitace je univerzální jev a že každý objekt s hmotou ve svém prostředí produkuje pole schopné vytvářet sílu na jiný.

Rejstřík článků
- 1 Vzorce a rovnice
- 2 Charakteristika gravitační energie
- 2.1 Gravitační pole a potenciál
- 3 Aplikace
- 3.1 Gravitační potenciál Země
- 3.2 Potenciální energie v blízkosti zemského povrchu
- 4 cvičení
- 4.1 Cvičení 1: Gravitační kolaps Země
- 4.2 Cvičení 2: Gravitační kolaps a úniková rychlost
- 4.3 Cvičení 3: Gravitační energie jablka
- 5 Reference
Vzorce a rovnice
Síla, kterou Newton označoval, je známá jako gravitační síla a dodává energii objektu, na který působí. Newton formuloval zákon univerzální gravitace takto:
„Nechť existují dva bodové objekty o hmotnosti m1 a m2, každý z nich vyvíjí na druhého přitažlivou sílu, která je úměrná součinu jejich hmot a nepřímo úměrná druhé mocnině vzdálenosti, která je odděluje“.
Gravitační energie NEBO spojené s gravitační silou F to je:

Objekt, který je ponořen do gravitačního pole, má gravitační potenciální energii NEBO a kinetická energie K.. Pokud neexistují žádné další interakce, nebo mají zanedbatelnou intenzitu, pak celková energie A uvedeného objektu je součet jeho gravitační energie plus jeho kinetické energie:
E = K + U
Pokud je předmět v gravitačním poli a nejsou přítomny žádné další disipativní síly, jako je tření nebo odpor vzduchu, pak celková energie A je množství, které během pohybu zůstává konstantní.
Charakteristika gravitační energie
- Objekt má gravitační potenciální energii, pokud je pouze v přítomnosti gravitačního pole produkovaného jiným.
- Gravitační energie mezi dvěma objekty se zvyšuje, protože je větší separační vzdálenost mezi nimi.
- Práce vykonaná gravitační silou je stejná a opačná k variaci gravitační energie konečné polohy vzhledem k její počáteční poloze..
- Pokud je těleso vystaveno pouze působení gravitace, pak je variace jeho gravitační energie stejná a opačná ke změně její kinetické energie..
- Potenciální energie hmotného objektu m který je ve výšce h vzhledem k zemskému povrchu je mgh krát větší než potenciální energie na povrchu, bytí G gravitační zrychlení, pro výšky h mnohem menší než pozemský poloměr.
Gravitační pole a potenciál
Gravitační pole G je definována jako gravitační síla F na jednotku hmotnosti. Stanoví se umístěním zkušební částice m do každého bodu v prostoru a výpočtem kvocientu mezi silou působící na zkušební částici dělenou hodnotou její hmotnosti:
G = F / m
Gravitační potenciál V objektu o hmotnosti m je definován jako gravitační potenciální energie tohoto objektu dělená jeho vlastní hmotou.
Výhodou této definice je, že gravitační potenciál závisí pouze na gravitačním poli, takže jakmile je potenciál známý PROTI, gravitační energie NEBO hromadného objektu m to je:
U = m.V.

Aplikace
Gravitační potenciální energie je energie uložená těly, když jsou v gravitačním poli.
Například voda obsažená v nádrži má více energie, protože nádrž je vyšší..
Čím vyšší je výška nádrže, tím větší je rychlost vody opouštějící kohoutek. To je způsobeno skutečností, že potenciální energie vody ve výšce nádrže se transformuje na kinetickou energii vody na výstupu z kohoutku..
Když je voda přehrazena na vrcholu hory, lze tuto potenciální energii využít k otočení turbín na výrobu energie..
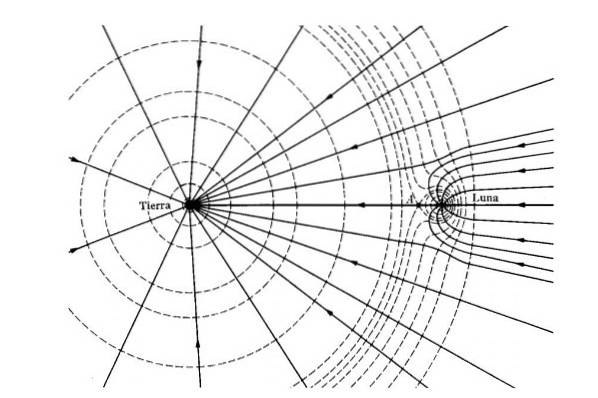
Gravitační energie také vysvětluje příliv a odliv. Vzhledem k tomu, že energie a gravitační síla závisí na vzdálenosti, je gravitační síla Měsíce větší na tváři Země nejblíže k Měsíci než na nejvzdálenější a opačné straně..
To vytváří rozdíl v silách, který deformuje mořský povrch. Účinek je větší u nového měsíce, když jsou Slunce a Měsíc vyrovnány.
Možnost výstavby vesmírných stanic a satelitů, které zůstávají relativně blízko naší planety, je dána gravitační energií produkovanou Zemí. Jinak by vesmírné stanice a umělé satelity toulali vesmírem.
Gravitační potenciál Země
Předpokládejme, že Země má hmotu M a objekt, který je nad zemským povrchem v dálce r vzhledem ke středu má hmotu m.
V tomto případě je gravitační potenciál určen z gravitační energie jednoduše dělené hmotou výsledného objektu:

Potenciální energie blízko zemského povrchu
Předpokládejme, že Země má poloměr RT a mše M.
Přestože Země není bodovým objektem, pole na jejím povrchu je ekvivalentní poli, které by bylo získáno, pokud by byla veškerá jeho hmotnost M byla koncentrována ve středu, takže gravitační energie objektu ve výšce h nad zemským povrchem je
U (R.T + h) = -G.M m (R.T + h) ^ - 1
Ale protože h je mnohem menší než RT, výše uvedený výraz lze aproximovat pomocí
U = Uo + mgh
Kde g je gravitační zrychlení, jehož průměrná hodnota pro Zemi je 9,81 m / s ^ 2.
Pak je potenciální energie Ep objektu o hmotnosti m ve výšce h nad zemským povrchem:
Ep (h) = U + Uo = mgh
Na zemském povrchu h = 0, takže objekt na povrchu má Ep = 0. Podrobné výpočty lze vidět na obrázku 3.

Výcvik
Cvičení 1: Gravitační kolaps Země
Předpokládejme, že naše planeta utrpí gravitační kolaps v důsledku ztráty tepelné energie v jejím nitru a její poloměr klesne na polovinu své současné hodnoty, ale hmotnost planety zůstává konstantní..
Určete, jaké by bylo gravitační zrychlení blízko povrchu Nové Země a kolik by vážil přeživší s hmotností 50 kg-f před zhroucením. Zvyšte nebo snižte gravitační energii osoby a o jaký faktor.
Řešení
Gravitační zrychlení na povrchu planety závisí na její hmotnosti a poloměru. Gravitační konstanta je univerzální a funguje stejně pro planety i exoplanety.
V tomto případě, pokud je poloměr Země snížen na polovinu, pak by gravitační zrychlení Nové Země bylo 4krát větší. Podrobnosti naleznete na následující desce.

To znamená, že nadčlověk a přeživší, který na staré planetě vážil 50 kg-f, bude na nové planetě vážit 200 kg-f..
Na druhou stranu bude gravitační energie na povrchu nové planety snížena na polovinu..
Cvičení 2: Gravitační kolaps a úniková rychlost
S ohledem na situaci uvedenou v cvičení 1, co by se stalo s únikovou rychlostí: zvyšuje, klesá, o jaký faktor?
Řešení 2
Úniková rychlost je minimální rychlost nezbytná k úniku z gravitačního působení planety.
Pro jeho výpočet se předpokládá, že projektil vystřelený touto rychlostí dosáhne nekonečna s nulovou rychlostí. Navíc v nekonečnu je gravitační energie nulová. Proto projektil vystřelený únikovou rychlostí bude mít nulovou celkovou energii.
Jinými slovy, na povrchu planety v době výstřelu musí být součet kinetické energie střely + gravitační energie nulový:
½ m Ve ^ 2 - (G M.m) / RT = 0
Všimněte si, že úniková rychlost nezávisí na hmotnosti střely a její hodnota na druhou je
Ve ^ 2 = (2G M) / R.T
Pokud se planeta zhroutí na poloměr poloviny původní, čtverec nové únikové rychlosti se zdvojnásobí.
Proto nová úniková rychlost roste a stává se 1,41násobkem staré únikové rychlosti:
Go '= 1,41 Go
Cvičení 3: Gravitační energie jablka
Chlapec na balkóně budovy 30 metrů nad zemí upustí 250 g jablka, které po několika sekundách dosáhne na zem.

a) Jaký je rozdíl gravitační energie jablka nahoře vzhledem k jablku na úrovni země?
b) Jak rychlé bylo jablko těsně před rozlitím na zem?
c) Co se stane s energií, jakmile se jablko srovná se zemí?
Řešení
a) Rozdíl gravitační energie je
m.g.h = 0,250 kg * 9,81 m / s ^ 2 * 30 m = 73,6 J
b) Potenciální energie, kterou jablko mělo, když byla vysoká 30 m, se přemění na kinetickou energii v době, kdy jablko dosáhne země.
½ m v ^ 2 = m.g.h
v ^ 2 = 2.g.h
Nahrazením hodnot a řešením vyplývá, že jablko dosáhne země rychlostí 24,3 m / s = 87,3 km / h.
c) Je zřejmé, že jablko je rozptýleno a veškerá gravitační energie nahromaděná na začátku je ztracena ve formě tepla, protože kousky jablka a nárazová zóna jsou zahřáté, navíc část energie je také rozptýlena ve formě zvuku vlny "stříkající".
Reference
- Alonso, M. (1970). Physics Vol.1, Meziamerický vzdělávací fond.
- Hewitt, Paul. 2012. Konceptuální fyzikální věda. 5. Ed. Pearson.
- Knight, R. 2017. Fyzika pro vědce a inženýrství: strategický přístup. Pearson.
- Sears, F. (2009). University Physics Vol.1
- Wikipedia. Gravitační energie. Obnoveno z: es.wikipedia.com
- Wikipedia. Gravitační energie. Obnoveno z: en.wikipedia.com



Zatím žádné komentáře