
Potenciální energetické charakteristiky, typy, výpočet a příklady
The potenciální energie Je to energie, kterou těla vlastní díky své konfiguraci. Když objekty interagují, existují mezi nimi síly schopné vykonávat práci a tato schopnost vykonávat práci, která je uložena v jejich dispozicích, může být převedena na energii..
Například lidé od nepaměti využívají potenciální energii vodopádů, nejprve v přádelnách a poté ve vodních elektrárnách..

Na druhou stranu má mnoho materiálů pozoruhodnou schopnost pracovat tím, že se deformují a poté se vrátí do své původní velikosti. A za jiných okolností uspořádání elektrického náboje umožňuje ukládání elektrické potenciální energie, například v kondenzátoru.
Potenciální energie nabízí mnoho možností, jak ji přeměnit na jiné formy využitelné energie, a proto je důležité znát zákony, které ji řídí..
Rejstřík článků
- 1 Původ potenciální energie
- 2 Druhy potenciální energie
- 2.1 Gravitační potenciální energie
- 2.2 Elastická potenciální energie
- 2.3 Elektrostatická potenciální energie
- 2.4 Jaderná potenciální energie
- 2.5 Chemická potenciální energie
- 3 Příklady potenciální energie
- 4 Výpočet potenciální energie
- 4.1 Výpočet gravitační potenciální energie
- 4.2 Výpočet elastické potenciální energie
- 4.3 Výpočet elektrostatické potenciální energie
- 5 Cvičení vyřešena
- 5.1 - Cvičení 1: pružina, která se táhne
- 5.2 - Cvičení 2: konzervativní a nekonzervativní síly
- 6 Reference
Původ potenciální energie
Potenciální energie objektu má původ v silách, které jej ovlivňují. Potenciální energie je však skalární velikosti, zatímco síly jsou vektorové. Proto k určení potenciální energie stačí uvést její číselnou hodnotu a vybrané jednotky.
Další důležitou vlastností je typ síly, s níž lze uložit potenciální energii, protože ne každá síla má tuto ctnost. Pouze konzervativní síly ukládají potenciální energii v systémech, na které působí.
Konzervativní síla je síla, u které práce nezávisí na dráze, kterou objekt následuje, ale pouze na počátečním a cílovém bodě. Síla, která pohání padající vodu, je gravitace, která je konzervativní silou.
Na druhou stranu elastické a elektrostatické síly mají také tuto kvalitu, proto s nimi souvisí potenciální energie..
Síly, které nesplňují výše uvedený požadavek, se nazývají nekonzervativní; jejich příkladem je tření a odpor vzduchu.
Druhy potenciální energie
Protože potenciální energie vždy pochází z konzervativních sil, jako jsou již zmíněné, hovoříme o gravitační potenciální energii, elastické potenciální energii, elektrostatické potenciální energii, jaderné potenciální energii a chemické potenciální energii..
Gravitační potenciální energie
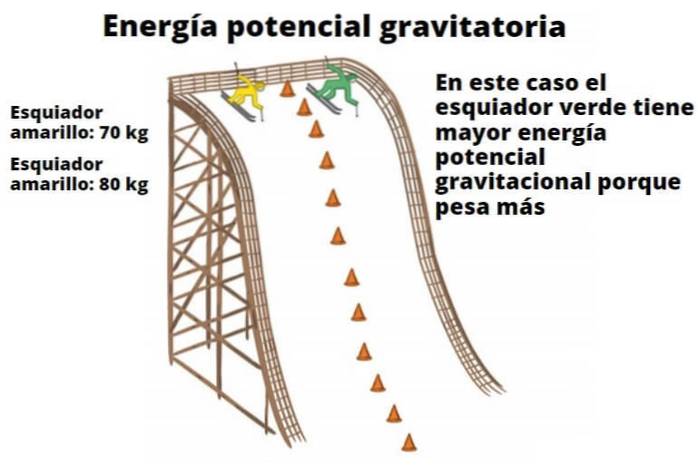
Každý objekt má potenciální energii jako funkci své výšky od země. Tento zdánlivě jednoduchý fakt ilustruje, proč je padající voda schopná pohánět turbíny a nakonec se transformovat na elektrickou energii. Zde zobrazený příklad lyžařů také ukazuje vztah hmotnosti a výšky k gravitační potenciální energii.
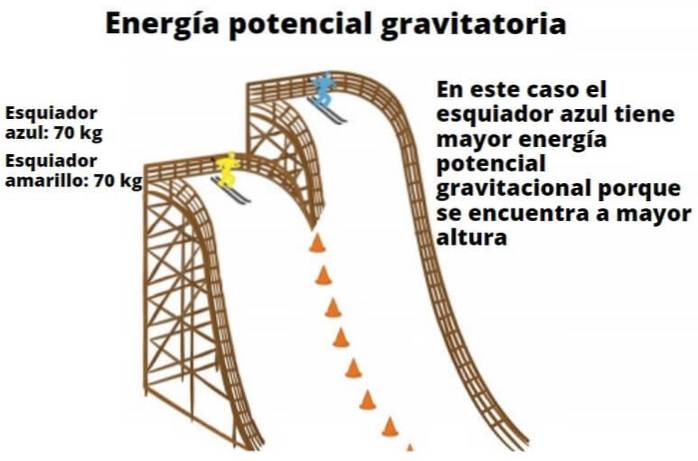
Dalším příkladem je auto na horské dráze, které má vyšší potenciální energii, když je v určité výšce nad zemí. Jakmile dosáhne úrovně terénu, jeho výška se rovná nule a veškerá jeho potenciální energie byla přeměněna na kinetickou energii (energii pohybu).
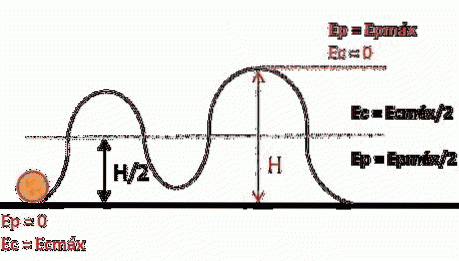
Elastická potenciální energie
Předměty, jako jsou pružiny, luky, kuše a gumičky, jsou schopné uchovávat elastickou potenciální energii..

Pružnost těla nebo materiálu je popsána Hookeovým zákonem (až do určitých mezí), který nám říká, že síla schopná vyvinout, když je stlačena nebo roztažena, je úměrná její deformaci.
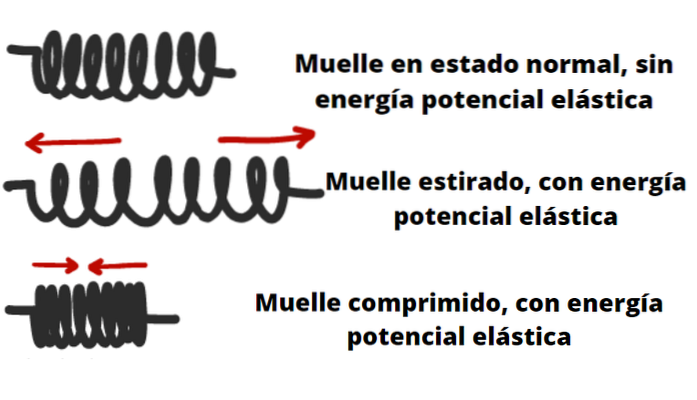
Například v případě pružiny nebo pružiny to znamená, že čím více se zmenšuje nebo táhne, tím větší sílu může vyvinout na předmět umístěný na jednom konci..
Elektrostatická potenciální energie
Je to energie, kterou mají elektrické náboje na základě své konfigurace. Elektrické náboje stejného znaménka se navzájem odpuzují, takže k umístění dvojice kladných nebo záporných nábojů do určité polohy musí externí agent pracovat. Jinak by měli tendenci se oddělovat.
Tato práce je uložena tak, jak byly umístěny břemena. Čím blíže jsou náboje stejného znaménka, tím vyšší potenciální energie bude mít konfigurace. Pokud jde o spoustu různých znaků, stane se opak; jak přitahují, čím blíže jsou, tím méně potenciální energie mají.
Jaderná potenciální energie
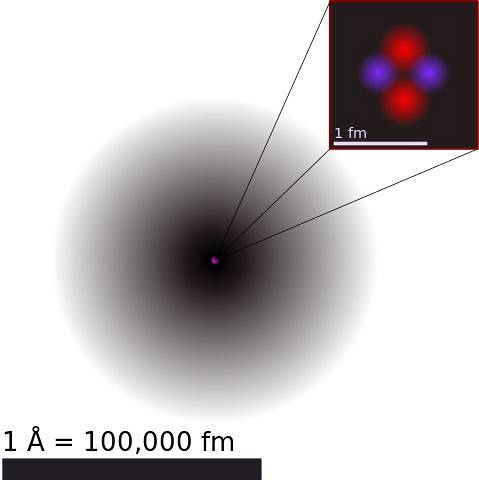
Atomové jádro je tvořeno obecně protony a neutrony nukleony. První mají kladný elektrický náboj a druhé jsou neutrální..
Jelikož jsou aglomerovány v malém prostoru mimo představivost a protože vědí, že náboje stejného znaménka se navzájem odpuzují, člověk si klade otázku, jak zůstává atomové jádro soudržné.
Odpověď spočívá v jiných silách než elektrostatickém odpuzování, typických pro jádro, jako je silná jaderná interakce a slabá jaderná interakce. Jedná se o velmi silné síly, které daleko převyšují elektrostatickou sílu.
Chemická potenciální energie
Tato forma potenciální energie pochází z toho, jak jsou uspořádány atomy a molekuly látek, podle různých typů chemických vazeb..
Když dojde k chemické reakci, může být tato energie přeměněna na jiné typy, například pomocí baterie nebo elektrické baterie.
Příklady potenciální energie
Potenciální energie je v každodenním životě přítomna mnoha způsoby. Pozorování jeho účinků je stejně snadné jako umístit jakýkoli předmět do určité výšky a mít jistotu, že se může kdykoli kutálet nebo spadnout.
Zde jsou některé projevy dříve popsaných typů potenciální energie:
-Horské dráhy
-Auta nebo koule se valí z kopce

-Luky a šípy
-Elektrické baterie
-Hodinové kyvadlo

-Houpačka na houpačce
-Skočte na trampolínu
-Pomocí zatahovacího pera.
Viz: příklady potenciální energie.
Výpočet potenciální energie
Potenciální energie závisí na práci odvedené silou a ta zase nezávisí na trajektorii, takže lze konstatovat, že:
-Pokud jsou A a B dva body, práce ŽAB nutné přejít z bodu A do bodu B se rovná práci potřebné k přechodu z bodu B do bodu A. Proto: ŽAB = WBA, tak:
ŽAB + ŽBA = 0
-A pokud se pokusí spojit dvě různé trajektorie 1 a 2 s uvedenými body A a B, práce provedená v obou případech je také stejná:
Ž1 = Wdva.
V obou případech objekt zažije změnu potenciální energie:
Změna = konečná potenciální energie - počáteční potenciální energie
ΔU = Ufinále - NEBOpočáteční = UB - NEBONA
Potenciální energie objektu je definována jako negativ práce provedené (konzervativní) silou:
ΔU = -WAB
Ale protože práce je definována tímto integrálem:


Všimněte si, že jednotky potenciální energie jsou stejné jako jednotky práce. V mezinárodním systému SI je jednotkou joule, který je zkrácen J a je ekvivalentní 1 newton x metr, anglický fyzik James Joule (1818-1889).
Mezi další energetické jednotky patří cgs erg, libra síla x noha, BTU (Britská tepelná jednotka), kalorie a kilowatthodiny.
Podívejme se níže na některé konkrétní případy, jak vypočítat potenciální energii.
Výpočet gravitační potenciální energie
V blízkosti zemského povrchu gravitační síla směřuje svisle dolů a její velikost je dána rovnicí Hmotnost = hmotnost x gravitace.
Označíme svislou osu písmenem „y“ a přiřadíme tomuto směru jednotkový vektor j, pozitivní nahoru a negativní dolů, změna potenciální energie při pohybu těla y = yNA dokud y = yB to je:

U (y) = mgy
Výpočet elastické potenciální energie
Hookeův zákon nám říká, že síla je úměrná deformaci:
F = -k.x.
Tady X je deformace a k je vlastní konstanta pružiny, která udává, jak je tuhá. Prostřednictvím tohoto výrazu se vypočítá elastická potenciální energie, s přihlédnutím k tomu i je jednotkový vektor ve vodorovném směru:

U (x) = ½ kxdva
Výpočet elektrostatické potenciální energie
Když máte bodový elektrický náboj Q, produkuje elektrické pole, které vnímá další bodový náboj co, a že na něm funguje, když je přesunut z jedné pozice do druhé uprostřed pole. Elektrostatická síla mezi dvěma bodovými náboji má radiální směr, symbolizovaný jednotkovým vektorem r:



Vyřešená cvičení
- Cvičení 1: pružina, která se táhne
Pružina, jejíž konstanta je k = 10,0 N / cm se zpočátku táhne 1,00 cm od své rovnovážné délky. Budete požádáni o výpočet dodatečné energie potřebné k natažení pružiny až o 5,00 cm nad její rovnovážnou délku..
Řešení
Přímým dosazením x = 1,00 cm do rovnice pro U (x) získáme N.cm, ale centimetry je nutné převést na metry, abychom získali energii v joulech:
U (1) = 0,5 x 10,0 N / cm x (1,00 cm)dva = 5 N. cm = 0,05 J; U (5) = 0,5 x 10,0 N / cm x (5,00 cm)dva = 125 N.cm = 1,25 J
Hledaný energetický rozdíl je tedy 1,25 - 0,05 J = 1,20 J.
- Cvičení 2: konzervativní a nekonzervativní síly
Malý blok se uvolní z klidu z bodu A, aby se posunul po beztřičné zakřivené rampě do bodu B. Odtud vstoupí na dlouhou drsnou vodorovnou plochu s dynamickým koeficientem tření μk = 0,2. Zjistěte, jak daleko od bodu B se zastaví, za předpokladu, že hNA= 3 m.

Řešení
Když je blok ve výšce hNA Vzhledem k zemi má díky své výšce gravitační potenciální energii. Po uvolnění se tato potenciální energie postupně přeměňuje na kinetickou energii a jak klouže po hladké zakřivené rampě, její rychlost se zvyšuje..
Během cesty z A do B nelze použít rovnice rovnoměrně proměnného přímočarého pohybu. I když je gravitace zodpovědná za pohyb bloku, pohyb, který prožívá, je složitější, protože trajektorie není přímočará.
Úspora energie v cestě AB
Jelikož je však gravitace konzervativní silou a na rampě nedochází k žádnému tření, můžete k zachování rychlosti na konci rampy použít zachování mechanické energie:
Mechanická energie v A = Mechanická energie v B
m.g.h.NA + ½ m.v.NAdva = m.g.h.B + ½ m.v.Bdva
Výraz je zjednodušen tím, že se v každém termínu objeví masa. Je uvolněn z odpočinku vNA = 0. A hB je na úrovni země, hB = 0. S těmito zjednodušeními se výraz redukuje na:
protiBdva = ghNA
Práce provedená třením v sekci BC
Nyní blok začíná svou cestu v drsném úseku touto rychlostí a nakonec se zastaví v bodě C. Proto vC = 0. Mechanická energie již není zachována, protože tření je disipativní síla, která vykonala práci na bloku danou:
Ždotek = - třecí síla x ujetá vzdálenost
Tato práce má negativní znaménko, protože kinetické tření zpomaluje objekt a brání jeho pohybu. Velikost kinetického tření Fk to je:
Fk = μk .N
Kde N je velikost normálové síly. Normálová síla je vyvíjena povrchem na blok, a protože je povrch zcela vodorovný, vyvažuje váhu P = mg, velikost normálu je tedy:
N = mg
Což vede k:
Fk = μk .mg
Práce to Fk dělá o bloku: Žk = - fk .D = - μk .mg.D.
Výpočet změny mechanické energie
Tato práce je ekvivalentní s změna mechanické energie, vypočteno takto:
Mechanická energie v C - Mechanická energie v B =
ΔEm = (UC +K.C) - (NEBOB + K.B) = - μk .mg.D
V této rovnici jsou některé termíny, které mizí: K.C = 0, protože blok se zastaví na C a U také zmizíC = UB, protože tyto body jsou na úrovni země. Výsledkem zjednodušení je:
- K.B = - μk .m.g.D
½ m.v.Bdva = μk .m.g.D
Hmota se opět ruší a D lze získat následujícím způsobem:
D = (½ vBdva) / (μk . g) = (½ vBdva) / (μk . g) = (½g.hNA) / (μk . g) = (½ hodinyNA) / μk = 0,5 x 3 m / 0,2 = 7,5 m
Reference
- Bauer, W. 2011. Fyzika pro inženýrství a vědy. Svazek 1. Mc Graw Hill.
- Figueroa, D. (2005). Série: Fyzika pro vědu a techniku. Svazek 2. Dynamika. Upravil Douglas Figueroa (USB).
- Giancoli, D. 2006. Fyzika: Principy s aplikacemi. 6.. Hala Ed Prentice.
- Knight, R. 2017. Fyzika pro vědce a inženýrství: strategický přístup. Pearson.
- Sears, Zemansky. 2016. Univerzitní fyzika s moderní fyzikou. 14. Vydání Volume 1-2.


Zatím žádné komentáře