V mechanice je předmět uvnitř nestabilní rovnováha když jej mírným posunutím ze své polohy pomocí síly nevrátí zpět. Například míč na následujícím obrázku, když je nad mohylou, je v nestabilní rovnováze, protože sebemenší porucha způsobí, že se bude valit z kopce bez možnosti návratu vlastními prostředky.
Naproti tomu, když je míč na rovném povrchu, jako ve střední poloze, říká se o něm lhostejný zůstatek nebo neutrální. Lze použít rušivou sílu, která ji posune na jednu nebo druhou stranu, ale pokud síla zmizí, míč se znovu stabilizuje.
Nakonec je míč vpravo na dně konkávní nádoby. Tato pozice je také vyvážená, ale stabilní rovnováha. Síla, která vyruší míč, způsobí, že bude jen trochu kmitat kolem původní polohy, aby se k ní nakonec tiše vrátila..
Rejstřík článků
Běžné předměty (a lidé a zvířata) ztrácejí rovnováhu a padají kvůli točivému momentu způsobenému váhou, silou, kterou Země vyvíjí na všechny objekty v blízkosti svého povrchu. Pokud máte rozšířené tělo, nazývá se bod, kde působí váha gravitační centrum.
Hmotnost může být vyvážena díky podpoře, jakou poskytuje povrch, a tímto způsobem se objekt nebude pohybovat. Ale i přesto má stále možnost otočit se o nějaký bod, protože v rozšířených objektech není rovnováha sil jediným faktorem, který je udržuje v klidu, ale také místem, kde jsou tyto síly aplikovány..
Níže je postava s tužkou vyváženou na špičce, v nestabilním vyvážení. Jakýkoli tah vzduchu způsobí jeho převrácení, ale mezitím se hmotnost a normální podpůrná síla navzájem vyrovnaly. Kromě toho mají obě síly stejnou linii působení, která prochází špičkou tužky a zajišťuje rovnováhu..
Pokud je však tužka trochu nakloněna, jak je znázorněno vpravo, linie působení závaží přestane procházet špičkou, která funguje jako čep. Poté váha vytváří nevyvážený točivý moment a dotek se otáčí ve směru hodinových ručiček..
Stabilní rovnováha je téměř vždy hledána, protože nestabilní rovnováha je, jak naznačuje její název, poměrně nejistá. Pokračujeme příkladem tužky, jakmile spadne a vodorovně se opře o povrch, je nová poloha mnohem stabilnější, než když stála na špičce..
To je způsobeno skutečností, že na jedné straně je těžiště blíže k povrchu a na druhé straně je nosná plocha tužky mnohem větší..
Když je nosná plocha větší, je větší pravděpodobnost, že normální bude schopna působit proti hmotnosti, protože povrch je přesně to, co normální působí. A pokud je vzdálenost od těžiště k povrchu menší, rameno páky závaží je menší a následně je také menší točivý moment..
Závěrem lze říci, že čím větší je podpěrná základna objektu a čím blíže je jeho těžiště k zemi, tím nižší je pravděpodobnost převrácení a rovnováha má tendenci být stabilní. Děti to vědí, a proto mají tendenci plazit se nejprve, než riskují, že vstanou.
A pokud je místo toho, aby bylo tělo podepřeno, je zavěšeno v bodě, hraje důležitou roli při stanovení rovnováhy také poloha těžiště, jak bude brzy ukázáno v následujících příkladech.
Rovnováha v podporovaných tělesech závisí, jak již bylo řečeno, na:
-Jak blízko je těžiště od povrchu.
-Velikost základny objektu.
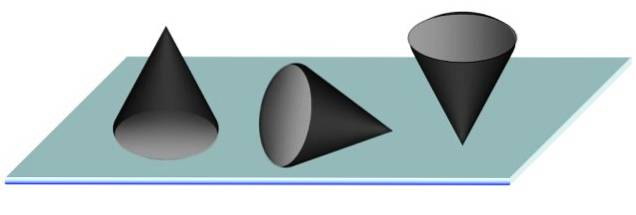
Zvažte kužel na plochém stole. Nejstabilnější poloha je bezpochyby se základnou kužele plně podepřenou na stole. Toto je stabilní rovnovážná poloha, protože těžiště kužele je na ose symetrie a blíže k jeho základně než ke špičce..
Lhostejné rovnováhy je dosaženo položením kužele vleže a nestabilní rovnováha odpovídá kužele na jeho špičce, jako tužka, což nemusí být snadný úkol, protože při nejmenším pohybu se kužel převrhne.
Je běžné najít zavěšená těla, která visí alespoň z jednoho bodu, například obrazy a lampy. Při ustavování rovnováhy zvažte umístění těžiště a umístění závěsného bodu..
Situaci lze snadno vizualizovat pomocí obdélníkového kartonu nebo pravidla homogenního materiálu. Zde se těžiště shoduje s geometrickým středem obrázku, že za předpokladu, že je hmotnost objektu rovnoměrně rozložena.
Aby se list dostal do nestabilní rovnováhy, je zavěšen z bodu, který je pod těžiště můžete dokonce list volně držet mezi prsty, abyste měli svobodu pohybu.
K okamžitému otáčení čepele v jednom nebo druhém směru stačí malá síla. Důvod otáčení je stejný jako v případě podporovaného předmětu: váha vyvíjí nekompenzovaný točivý moment, který usnadňuje otáčení těla.
Při otáčení list prochází polohou, která je ve stabilní rovnováze, ve které je bod zavěšení shora centrum gravitace. Kolem této polohy trochu osciluje a nakonec se zastaví.
Při opětovném použití síly čepel znovu osciluje, ale vrací se zpět do polohy, ve které jsou bod zavěšení a těžiště vyrovnány se svislou rovinou.
Nakonec je indiferentní rovnováha zkontrolována průchodem kolíku těsně přes těžiště. Pokud je list otočen tak, aby byl v různých polohách, je vidět, že mezi nimi nebude žádný zásadní rozdíl.
Závěrem lze říci, že u těles zavěšených v nestabilní rovnováze je bod zavěšení pod těžištěm. A naopak pro stabilní rovnováhu.
Zatím žádné komentáře