
Rovnice tepelné rovnováhy, aplikace, cvičení
Tepelná rovnováha dvou těles, která jsou v tepelném kontaktu, je stav, kterého je dosaženo po dostatečně dlouhé době, aby se teploty obou těles vyrovnaly.
V termodynamice je termální kontakt dvou těles (nebo dvou termodynamických systémů) chápán jako situace, ve které mají tělesa mechanický kontakt nebo jsou oddělená, ale v kontaktu s povrchem, který umožňuje pouze průchod tepla z jednoho tělesa do druhého (diatermický povrch).
-

Obrázek 1. Led a nápoj po chvíli dosáhnou své tepelné rovnováhy. Zdroj: Pixabay
Při tepelném kontaktu nesmí docházet k žádné chemické reakci mezi systémy, které jsou v kontaktu. Měla by existovat pouze výměna tepla.
Každodenní situace, ve kterých dochází k výměně tepla, se mimo jiné vyskytují u systémů, jako jsou studený nápoj a sklenice, horká káva a čajová lžička, nebo tělo a teploměr..
Rejstřík článků
- 1 Kdy jsou dva nebo více systémů v tepelné rovnováze??
- 2 Rovnice tepelné rovnováhy
- 2.1 Rovnovážná teplota
- 2.2 Tepelný kontakt se změnou fáze
- 3 Aplikace
- 3.1 - Cvičení 1
- 4 Vyřešená cvičení
- 4.1 - Cvičení 2
- 4.2 Cvičení 3
- 4.3 - Cvičení 4
- 5 Reference
Když jsou dva nebo více systémů v tepelné rovnováze?
Druhý zákon termodynamiky říká, že teplo vždy jde z těla s nejvyšší teplotou do těla s nejnižší teplotou. Přenos tepla přestane, jakmile se teploty vyrovnají a dosáhne se stavu tepelné rovnováhy..
Praktickou aplikací tepelné rovnováhy je teploměr. Teploměr je zařízení, které měří svou vlastní teplotu, ale díky tepelné rovnováze můžeme znát teplotu jiných těles, například osob nebo zvířat.
Rtuťový sloupcový teploměr je umístěn v tepelném kontaktu s tělem, například pod jazykem, a čeká se dost času na dosažení tepelné rovnováhy mezi tělem a teploměrem a jeho čtení se dále nemění.
Po dosažení tohoto bodu je teplota teploměru stejná jako teplota těla.
Nulový zákon termodynamiky říká, že pokud je těleso A v tepelné rovnováze s tělesem C a stejné těleso C je v tepelné rovnováze s B, pak jsou A a B v tepelné rovnováze, i když mezi A a B není tepelný kontakt..
Proto jsme dospěli k závěru, že dva nebo více systémů je v tepelné rovnováze, když mají stejnou teplotu.
Rovnice tepelné rovnováhy
Předpokládáme těleso A s počáteční teplotou Ta v tepelném kontaktu s jiným tělesem B s počáteční teplotou Tb. Předpokládáme také, že Ta> Tb, pak se podle druhého zákona teplo přenáší z A do B.
Po chvíli bude dosaženo tepelné rovnováhy a obě tělesa budou mít stejnou konečnou teplotu Tf. To bude mít střední hodnotu na Ta a Tb, tj. Ta> Tf> Tb.
Množství tepla Qa přeneseného z A do B bude Qa = Ma Ca (Tf - Ta), kde Ma je hmotnost tělesa A, Ca tepelná kapacita na jednotku hmotnosti A a (Tf - Ta) teplotní rozdíl. Pokud je Tf menší než Ta, pak je Qa záporná, což naznačuje, že tělo A se vzdává tepla.
Podobně pro tělo B máme Qb = Mb Cb (Tf - Tb); a pokud je Tf větší než Tb, pak je Qb kladné, což naznačuje, že tělo B přijímá teplo. Jelikož jsou těleso A a těleso B v tepelném kontaktu, ale izolovány od okolního prostředí, musí být celkové vyměněné teplo nulové: Qa + Qb = 0
Pak Ma Ca (Tf - Ta) + Mb Cb (Tf - Tb) = 0
Rovnovážná teplota
Vyvinutím tohoto výrazu a řešením pro teplotu Tf se získá konečná teplota tepelné rovnováhy.
-

Obrázek 2. Konečná rovnovážná teplota. Zdroj: vlastní výroba
Tf = (Ma Ca Ta + Mb Cb Tb) / (Ma Ca + Mb Cb).
V konkrétním případě zvažte případ, že tělesa A a B mají stejnou hmotnost a tepelnou kapacitu, v tomto případě bude rovnovážná teplota:
Tf = (Ta + Tb) / 2 ↔, pokud Ma = Mb a Ca = Cb.
Tepelný kontakt se změnou fáze
V některých situacích se stává, že když jsou dvě těla v tepelném kontaktu, tepelná výměna způsobí změnu stavu nebo fáze v jednom z nich. Pokud k tomu dojde, je třeba vzít v úvahu, že během fázové změny nedojde v těle ke změně teploty, která by změnila jeho stav.
Pokud dojde k fázové změně kteréhokoli z těles v tepelném kontaktu, použije se koncept latentního tepla L, což je energie na jednotku hmotnosti potřebnou pro změnu stavu:
Q = L ∙ M
Například k roztavení 1 kg ledu při 0 ° C je zapotřebí 333,5 kJ / kg a tato hodnota je latentní teplo L tání ledu.
Během tavení se mění z pevné vody na kapalnou vodu, ale tato voda si během procesu tavení udržuje stejnou teplotu jako led..
Aplikace
Tepelná rovnováha je součástí každodenního života. Podívejme se například na tuto situaci podrobně:
-Cvičení 1
Člověk se chce koupat v teplé vodě o teplotě 25 ° C. Do kbelíku vložte 3 litry studené vody o teplotě 15 ° C a v kuchyni ohřejte vodu na 95 ° C.
Kolik litrů horké vody byste měli přidat do kbelíku se studenou vodou, abyste dosáhli požadované konečné teploty?
Řešení
Předpokládejme, že A je studená voda a B je horká voda:
-
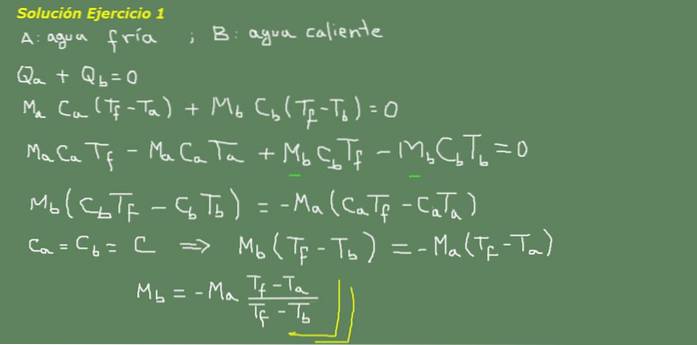
Obrázek 3. Řešení cvičení 3. Zdroj: vlastní zpracování.
Navrhujeme rovnici tepelné rovnováhy, jak je naznačeno na tabuli na obrázku 3 a odtud řešíme hmotnost vody Mb.
Počáteční množství studené vody lze získat, protože je známa hustota vody, která je 1 kg na litr. To znamená, že máme 3 kg studené vody.
Ma = 3 kg
Pak
Mb = - 3 kg * (25 ° C - 15 ° C) / (25 ° C - 95 ° C) = 0,43 kg
Pak stačí 0,43 litru horké vody, aby se konečně získalo 3,43 litru teplé vody při 25 ° C.
Vyřešená cvičení
-Cvičení 2
Kus kovu o hmotnosti 150 g a teplotě 95 ° C se vloží do nádoby obsahující půl litru vody při teplotě 18 ° C. Po chvíli se dosáhne tepelné rovnováhy a teplota vody a kovu je 25 ° C.
Předpokládejme, že nádoba s vodou a kovovým kusem je uzavřená termoska, která neumožňuje výměnu tepla s okolním prostředím.
Získejte specifické teplo kovu.
Řešení
Nejprve vypočítáme teplo absorbované vodou:
Qa = Ma Ca (Tf - Ta)
Qa = 500 g 1cal / (g ° C) (25 ° C - 18 ° C) = 3500 kalorií.
To je stejné teplo dané kovem:
Qm = 150 g Cm (25 ° C - 95 ° C) = -3500 kalorií.
Takže můžeme získat tepelnou kapacitu kovu:
Cm = 3500 cal / (150 g 70 ° C) = ⅓ cal / (g ° C).
Cvičení 3
Máte 250 c.c. vody při 30 ° C K této vodě, která je v izolační termosce, se při teplotě 0 ° C přidá 25 g kostek ledu za účelem jejího ochlazení.
Určete rovnovážnou teplotu; tj. teplota, která zůstane, jakmile se veškerý led roztaví a ledová voda se zahřeje, aby odpovídala teplotě vody ve sklenici zpočátku.
Řešení 3
Toto cvičení lze vyřešit ve třech fázích:
- Prvním je tání ledu, který absorbuje teplo z původní vody, aby se roztavil a stal se vodou..
- Poté se vypočítá pokles teploty v původní vodě, protože se vzdal tepla (Qced<0) para fundir el hielo.
- Nakonec musí být roztavená voda (pocházející z ledu) tepelně vyvážena s vodou, která původně existovala..
-

Obrázek 4. Řešení cvičení 3. Zdroj: vlastní zpracování.
Počítáme teplo potřebné k roztavení ledu:
Qf = L * Mh = 333,5 kJ / kg * 0,025 kg = 8,338 kJ
Potom je teplo dané vodou k roztavení ledu Qced = -Qf
Toto teplo vydávané vodou snižuje její teplotu na hodnotu T ', kterou můžeme vypočítat následovně:
T '= T0 - Qf / (Ma * Ca) = 22,02 ° C
Kde Ca je tepelná kapacita vody: 4,18 kJ / (kg ° C).
Nakonec původní hmotnost vody, která má nyní 22,02 ° C, se vzdá tepla hmotnosti roztavené vody z ledu, který má teplotu 0 ° C..
Nakonec bude rovnovážná teplota Te dosažena po dostatečné době:
Te = (Ma * T '+ Mh * 0 ° C) / (Ma + Mh) = (0,25 kg * 22,02 ° C + 0,025 kg * 0 ° C) / (0,25 kg + 0,025 kg).
Nakonec získání rovnovážné teploty:
Te = 20,02 ° C.
-Cvičení 4
Z pece vychází 0,5 kg kusu olova při teplotě 150 ° C, což je hluboko pod jeho teplotou tání. Tento kus se umístí do nádoby se 3 litry vody při pokojové teplotě 20 ° C. Určete konečnou rovnovážnou teplotu.
Vypočítejte také:
- Množství tepla dodaného olovem do vody.
- Množství tepla absorbovaného vodou.
Data:
Specifické teplo olova: Cp = 0,03 cal / (g ° C); měrné teplo vody: Ca = 1 cal / (g ° C).
Řešení
Nejprve určíme konečnou rovnovážnou teplotu Te:
Te = (Ma Ca Ta + Mp Cp Tp) / (Ma Ca + Mp Cp)
Te = 20,65 ° C
Množství tepla uvolněného olovem je pak:
Qp = Mp Cp (Te - Tp) = -1,94 x 10³ kal.
Množství tepla absorbovaného vodou bude:
Qa = Ma Ca (Te - Ta) = + 1,94x 10³ kal.
Reference
- Atkins, P. 1999. Fyzikální chemie. Edice Omega.
- Bauer, W. 2011. Fyzika pro inženýrství a vědy. Svazek 1. Mc Graw Hill.
- Giancoli, D. 2006. Fyzika: Principy s aplikacemi. 6.… Ed Prentice Hall.
- Hewitt, Paul. 2012. Konceptuální fyzikální věda. 5. Ed. Pearson.
- Resnick, R. (1999). Fyzický. Sv. 1. 3. vydání. Ve španělštině. Compañía Editorial Continental S.A. autor: C.V.
- Rex, A. 2011. Základy fyziky. Pearson.
- Sears, Zemansky. 2016. Univerzitní fyzika s moderní fyzikou. 14. Vydání Volume 1.
- Serway, R., Jewett, J. (2008). Fyzika pro vědu a techniku. Svazek 1. 7. Ed. Cengage Learning.


Zatím žádné komentáře