
Normální úsilí, z čeho se skládá, jak se počítá, příklady
The normální úsilí aplikovaný na určitý materiál, nazývaný také jednoosé napětí, je vztah, který existuje mezi silou působící kolmo na určitý povrch a plochou průřezu, na kterou působí, nebo zatížením na jednotku plochy. Matematicky, pokud P je velikost síly a A je oblast, kde je aplikována, napětí σ je kvocient: σ = P / A.
Jednotky normálového napětí v mezinárodním systému jsou newton / metrdva, známé jako Pascaly a zkráceně Pa. Jedná se o stejné jednotky tlaku. Dalšími jednotkami, které se v literatuře často vyskytují, jsou libry / palec.dva nebo psi.

Na obrázku 2 jsou dvě síly stejné velikosti aplikovány kolmo na plochu průřezu, čímž působí na tyč velmi lehký tah, který má sklon ji prodlužovat..
Tyto síly vytvářejí normální napětí, které se také nazývá axiální zatížení na střed, protože jeho linie působení se shoduje s osovou osou, na které leží těžiště.
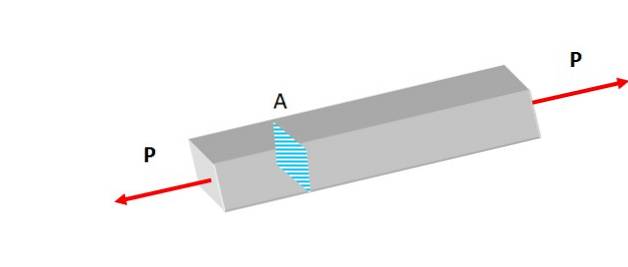
Snahy, ať už normální nebo jiné, se v přírodě neustále objevují. V litosféře jsou horniny vystaveny gravitaci a tektonické aktivitě, které podléhají deformacím.
Tímto způsobem vznikají struktury, jako jsou záhyby a poruchy, jejichž studium je důležité při těžbě nerostů a ve stavebnictví, pro konstrukci budov a silnic, abychom jmenovali jen několik příkladů..
Rejstřík článků
- 1 Jak se počítá?
- 2 Hookův zákon a normální stres
- 3 Důležitost napětí v pevnosti materiálů a geologii
- 4 příklady
- 4.1 - Cvičení 1
- 4.2 - Cvičení 2
- 5 Reference
Jak se to počítá?
Rovnice daná na začátku σ = P / A umožňuje vypočítat průměrné normální napětí v dané oblasti. Hodnota P je velikost výsledné síly na plochu aplikovanou na těžiště a je dostatečná pro mnoho jednoduchých situací.
V tomto případě je rozložení sil rovnoměrné, zejména v místech daleko od místa, kde je tyč vystavena napětí nebo tlaku. Pokud však potřebujete vypočítat napětí v určitém bodě nebo síly nejsou rovnoměrně rozloženy, měli byste použít následující definici:
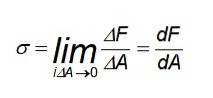
Obecně se tedy hodnota napětí v určitém bodě může lišit od průměrné hodnoty. Ve skutečnosti se úsilí může lišit v závislosti na uvažované sekci..
To je znázorněno na následujícím obrázku, na kterém se tahové síly F pokusí oddělit rovnovážnou tyč v řezech mm Y nn.
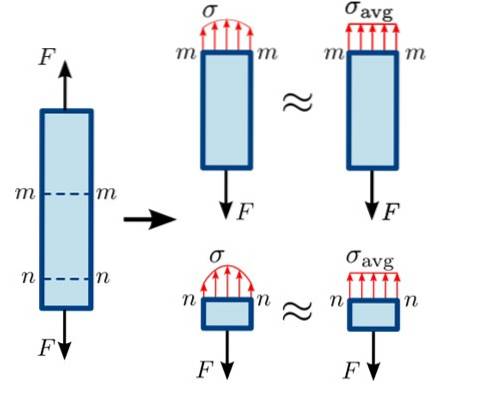
Jako sekce nn je velmi blízko místa, kde je síla F aplikována směrem dolů, rozložení sil na povrchu není zcela homogenní, čím nižší je síla, tím dále od tohoto bodu. Distribuce je v sekci o něco homogennější mm.
V každém případě má normální snaha vždy tendenci protáhnout nebo stlačit dvě části těla, které jsou na obou stranách roviny, na kterou působí. Na druhou stranu, jiné různé snahy, jako je stříhání, mají tendenci tyto části přemísťovat a oddělit..
Hookeův zákon a normální stres
Hookeův zákon stanoví, že v mezích pružnosti je normální napětí přímo úměrné deformaci, kterou zažívá tyč nebo předmět. V tom případě:
Normální úsilí ∝ Deformace jednotky
Být konstantou proporcionality Youngův modul (Y):
Normálové napětí (σ) = Youngův modul (Y) x jednotkové přetvoření (ε)
σ = Y. ε
S ε = ΔL / L, kde ΔL je rozdíl mezi konečnou a počáteční délkou, což je L.
Youngův modul nebo modul pružnosti je charakteristikou materiálu, jehož rozměry jsou stejné jako u napětí, protože jednotkové přetvoření je bezrozměrné.
Důležitost napětí v pevnosti materiálů a geologii
Stanovení odolnosti materiálů vůči stresu je velmi důležité. U konstrukcí používaných při stavbě budov i při navrhování dílů pro různá zařízení je třeba zajistit, aby zvolené materiály adekvátně plnily svou funkci.
Z tohoto důvodu jsou materiály v laboratořích vyčerpávajícím způsobem analyzovány pomocí testů, jejichž cílem je zjistit, kolik síly vydrží před deformací a rozbitím, čímž ztratí svou funkci. Na základě toho se rozhoduje, zda jsou nebo nejsou vhodné k výrobě určité součásti nebo tvoří součást zařízení..
Předpokládá se, že prvním vědcem, který systematicky studoval sílu materiálů, byl Leonardo Da Vinci. Zanechal důkazy o testech, ve kterých určoval odpor drátů zavěšením kamenů různých hmotností.
Při tomto úsilí je důležitá jak velikost síly, tak i rozměry konstrukce a způsob jejího použití, aby bylo možné stanovit meze, v nichž má materiál elastické chování; to znamená, že se vrátí do své původní podoby, když úsilí přestane.
Na základě výsledků těchto zkoušek se vytvářejí křivky napětí-deformace pro různé typy materiálů, jako je ocel, beton, hliník a mnoho dalších..
Příklady
Následující příklady předpokládají, že síly jsou rovnoměrně rozloženy a že materiál je homogenní a izotropní. To znamená, že jejich vlastnosti jsou v obou směrech stejné. Proto je platné použít k nalezení sil rovnici σ = P / A.
-Cvičení 1
Na obrázku 3 je známo, že průměrné normální napětí působící na úsek AB má velikost 48 kPa. Najít: a) Velikost síly F působící na CB, b) Napětí v řezu BC.
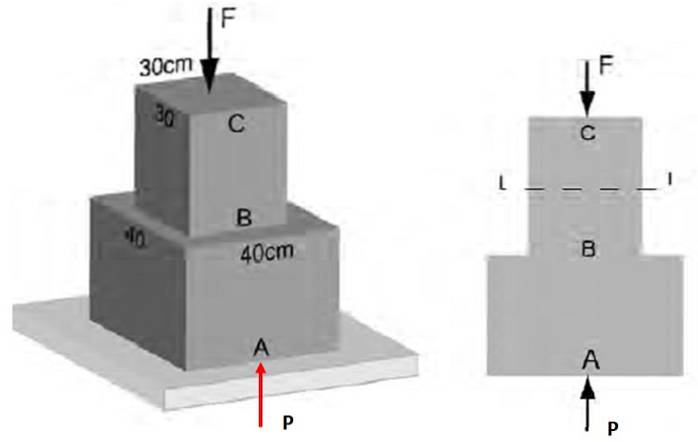
Řešení
Vzhledem k tomu, že struktura je ve statické rovnováze, podle druhého Newtonova zákona:
P-F = 0
Normální napětí na úseku AB má velikost:
σAB = P / AAB
Odkud P = σAB . NAAB = 48 000 Pa. (40 x 10 -dva m)dva = 7680 N
Proto F = 7680 N
Normální napětí v řezu BC je kvocient mezi velikostí F a plochou průřezu této strany:
σpřed naším letopočtem = F / Apřed naším letopočtem = 7680 N / (30 x 10 -dva m)dva = 85,3 kPa.
-Cvičení 2
Drát o délce 150 m a průměru 2,5 mm je natažen silou 500 N.
a) Podélné napětí σ.
b) Jednotkové přetvoření s vědomím, že konečná délka je 150,125 m.
c) Modul pružnosti Y tohoto drátu.
Řešení
a) σ = F / A = F / π.rdva
Poloměr drátu je poloviční průměr:
r = 1,25 mm = 1,25 x 10-3 m.
Plocha průřezu je π.rdva, pak je snaha:
σ = F / π.rdva = 500 / (π. (1,25 x 10-3)dva Pa = 101859,2 Pa
b) ε = ΔL / L = (konečná délka - počáteční délka) / počáteční délka
Proto:
ε = (150,125 - 150) / 150 = 0,125 / 150 = 0,000833
c) Youngův modul drátu je vyřešen s vědomím dříve vypočítaných hodnot ε a σ:
Y = σ / ε = 101859,2 Pa / 0,000833 = 1,22 x 108 Pa = 122 MPa.
Reference
- Beer, F. 2010. Mechanika materiálů. 5. Edice. McGraw Hill. 7 - 9.
- Giancoli, D. 2006. Fyzika: Principy s aplikacemi. 6tth Ed. Prentice Hall. 238-242.
- Hibbeler, R.C. 2006. Mechanika materiálů. 6.. Edice. Pearson Education. 22-25
- Valera Negrete, J. 2005. Poznámky k obecné fyzice. UNAM. 87-98.
- Wikipedia. Stres (mechanika). Obnoveno z: wikipedia.org.



Zatím žádné komentáře