Hovoří se o náhodný experiment když je výsledek každého konkrétního hodnocení nepředvídatelný, i když lze určit pravděpodobnost výskytu konkrétního výsledku.
Mělo by však být objasněno, že není možné reprodukovat stejný výsledek náhodného systému se stejnými parametry a počátečními podmínkami v každém pokusu experimentu..
Dobrým příkladem náhodného experimentu je válcování kostkou. I když je třeba dbát na to, aby se kostka hodila stejným způsobem, každý pokus přinese nepředvídatelný výsledek. Jediné, co lze říci, je, že výsledkem může být jeden z následujících: 1, 2, 3, 4, 5 nebo 6.
Hod mincí je dalším příkladem náhodného experimentu, který má pouze dva možné výsledky: hlavy nebo ocasy. Ačkoliv je mince hozena ze stejné výšky a stejným způsobem, faktor šance bude vždy přítomen, což při každém novém pokusu povede k nejistotě..
Opakem náhodného experimentu je deterministický experiment. Například je známo, že pokaždé, když se voda vaří na hladině moře, je teplota varu 100 ° C. Nikdy se však nestane, že při stejných podmínkách bude výsledek někdy 90 ° C, jiný 12 0 ° C a někdy 100 ° C..
Rejstřík článků
Je volána množina všech možných výsledků náhodného experimentu ukázkový prostor. V náhodném experimentu s válcováním kostky je ukázkový prostor:
D = 1, 2, 3, 4, 5, 6.
Na druhé straně, v hodu mincí je ukázkový prostor:
M = hlavy, razítko.
V náhodném experimentu, a událost je to výskyt určitého výsledku či nikoli. Například v případě hodu mincí je událostí nebo událostí to, že se objeví hlavy.
Další událostí v náhodném experimentu může být následující: že na roli kostky se hodí číslo menší nebo rovné třem.
V případě, že dojde k události, pak sada možných výsledků je sada:
E = 1, 2, 3
Na druhé straně se jedná o podmnožinu ukázkového prostoru nebo sady:
M = 1, 2, 3, 4, 5, 6.
Zde je několik příkladů, které ilustrují výše uvedené:
Předpokládejme, že jsou hozeny dvě mince, jedna po druhé. Ptá se:
a) Uveďte, zda se jedná o náhodný experiment nebo naopak o deterministický experiment.
b) Jaký je ukázkový prostor S tohoto experimentu?
c) Uveďte množinu události A, která odpovídá skutečnosti, že výsledkem experimentu jsou hlavy a ocasy.
d) Vypočítejte pravděpodobnost, že dojde k události A..
e) Nakonec najděte pravděpodobnost, že dojde k události B: ve výsledku se neobjeví žádné hlavy.
a) Jde o náhodný experiment, protože neexistuje způsob, jak předpovědět, jaký bude výsledek losování dvou mincí.
b) Ukázkový prostor je souborem všech možných výsledků:
S = (c, c), (c, s), (s, c), (s, s)
c) Událost A, pokud k ní dojde, může mít následující výsledky:
A = (c, s), (s, c)
d) Pravděpodobnost, že dojde k události A, se získá vydělením počtu prvků množiny A počtem prvků množiny S odpovídajících vzorovému prostoru:
P (A) = 2/4 = ½ = 0,5 = 50%
e) Soubor možných výsledků odpovídajících události B (ve výsledku se neobjevující hlavy) je:
B = (s, s)
Pravděpodobnost, že k události B dojde v pokusu, je tedy podíl mezi počtem možných výsledků B a počtem celkových případů:
P (B) = ¼ = 0,25 = 25%.
Taška obsahuje 10 bílých kuliček a 10 černých kuliček. Tři kuličky po sobě jsou vyňaty z vaku náhodně a bez pohledu dovnitř.
a) Určete prostor vzorku tohoto náhodného experimentu.
b) Určete množinu výsledků odpovídající události A, která spočívá v tom, že po experimentu budou dva černé kuličky.
c) Událostí B je získat alespoň dva černé kuličky, určit množinu B výsledků pro tuto událost.
d) Jaká je pravděpodobnost, že dojde k události A.?
e) Najděte pravděpodobnost, že dojde k události B..
f) Určete pravděpodobnost, že výsledkem náhodného experimentu bude, že máte alespoň jeden černý mramor. Tato událost se bude jmenovat C.
Pro konstrukci ukázkového prostoru je užitečné vytvořit stromový diagram, jako je ten, který je znázorněn na obrázku 3:
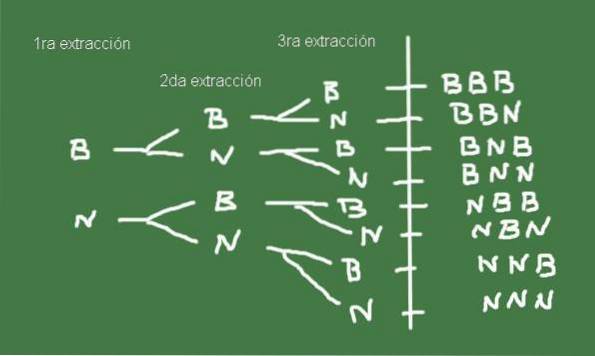
Sada Ω možných výsledků extrakce tří kuliček ze sáčku se stejným počtem černých a bílých kuliček je přesně ukázkovým prostorem tohoto náhodného experimentu.
Ω = (b, b, b), (b, b, n), (b, n, b), (b, n, n), (n, b, b), (n, b, n) , (n, n, b), (n, n, n)
Sada možných výsledků odpovídající události A, která spočívá v tom, že má dva černé kuličky, je:
A = (b, n, n), (n, b, n), (n, n, b)
Událost B je definována jako: „mít alespoň dva černé kuličky poté, co náhodně vytáhl tři z nich“. Soubor možných výsledků pro událost B je:
B = (b, n, n), (n, b, n), (n, n, b), (n, n, n)
Pravděpodobnost výskytu události A je podíl mezi počtem možných výsledků pro tuto událost a celkovým počtem možných výsledků, tj. Počtem prvků ve vzorovém prostoru.
P (A) = n (A) / n (Ω) = 3/8 = 0,375 = 37,5%
Existuje tedy 37,5% šance mít dva černé kuličky po náhodném vytažení tří kuliček z vaku. Všimněte si však, že v žádném případě nemůžeme předpovědět přesný výsledek experimentu.
Pravděpodobnost, že dojde k události B, spočívající v získání alespoň jednoho černého mramoru, je:
P (B) = n (B) / n (Ω) = 4/8 = 0,5 = 50%
To znamená, že možnost, že dojde k události B, se rovná pravděpodobnosti, že k ní nedojde.
Pravděpodobnost získání alespoň jednoho černého mramoru se po vytěžení tří z nich rovná 1 minus pravděpodobnost, že výsledkem budou „tři bílé kuličky“.
P (C) = 1 - P (b b b) = 1 - ⅛ = ⅞ = 0,875 = 87,5%
Nyní můžeme tento výsledek zkontrolovat a poznamenat, že počet možností, ke kterým dojde k události C, se rovná počtu prvků možných výsledků pro událost C:
C = (b, b, n), (b, n, b), (b, n, n), (n, b, b), (n, b, n), (n, n, b) , (n, n, n)
n (C) = 7
P (C) = n (C) / n (Ω) = ⅞ = 87,5%
Zatím žádné komentáře