
Vzorce odstředivé síly, jak ji vypočítat, příklady, cvičení
The odstředivá síla má tendenci vytlačovat otáčející se těla kolem křivky. Je to považováno za fiktivní síla, pseudoforce nebo setrvačná síla, protože to není způsobeno interakcemi mezi skutečnými objekty, ale je to projev setrvačnost těl. Setrvačnost je vlastnost, díky které si objekty chtějí zachovat klidový stav nebo rovnoměrný přímočarý pohyb, pokud ho mají..
Termín „odstředivá síla“ vytvořil vědec Christian Huygens (1629-1695). Uvedl, že křivočarý pohyb planet by je měl tendenci vzdalovat, pokud by Slunce nevyvíjelo nějakou sílu, aby je zadržovalo, a vypočítal, že tato síla byla úměrná druhé mocnině rychlosti a nepřímo úměrná poloměru popsaného obvodu..

Pro ty, kteří cestují autem, není odstředivá síla vůbec fiktivní. Cestující v autě, které se otáčí vpravo, se cítí tlačeni doleva a naopak, když auto zatáčí doleva, lidé zažívají sílu vpravo, která se zdá, že je chce posunout pryč od středu zatáčky.
Velikost odstředivé síly FG se vypočítá pomocí následujícího výrazu:
-FG je velikost odstředivé síly
-m je hmotnost objektu
-proti je rychlost
-R je poloměr zakřivené dráhy.
Síla je vektor, proto se pro její rozlišení od velikosti, která je skalární, používá tučný typ.
To musíte mít vždy na paměti FG se zobrazí, pouze když je pohyb popsán pomocí zrychleného referenčního snímku.
V příkladu popsaném na začátku představuje rotující vůz zrychlenou referenci, protože vyžaduje dostředivé zrychlení, abych se mohl otočit.
Rejstřík článků
- 1 Jak vypočítáte odstředivou sílu?
- 1.1 Schéma volného těla v setrvačném a neinerciálním systému
- 2 Příklady
- 3 cvičení
- 3.1 Cvičení 1
- 3.2 Cvičení 2
- 4 Aplikace
- 4.1 Odstředivky
- 4.2 Podložky
- 4.3 Převýšení křivek
- 5 Reference
Jak vypočítáte odstředivou sílu?
Volba referenčního systému je zásadní pro zhodnocení pohybu. Zrychlený referenční rámec je také známý jako neinerciální rámec..
V tomto typu systému, jako točící se auto, se objevují fiktivní síly, jako je odstředivá síla, jejichž původ není skutečnou interakcí mezi objekty. Cestující nemůže říci, co ho tlačí ze zatáčky, může pouze potvrdit, že tomu tak je.
Na druhou stranu, v inerciálním referenčním systému dochází k interakcím mezi skutečnými objekty, jako je těleso v pohybu, a Zemí, které způsobují váhu, nebo mezi tělesem a povrchem, na kterém se pohybuje, které způsobují tření a normální.
Dobrým příkladem inerciálního referenčního systému je pozorovatel stojící na kraji silnice a sledující zatáčení vozu. U tohoto pozorovatele auto zatáčí, protože na něj působí síla směřující do středu zatáčky, která ho nutí neopustit. Je to o dostředivá síla vytvářená třením mezi pneumatikami a vozovkou.
V setrvačném referenčním rámci se odstředivá síla neobjevuje. Prvním krokem k jeho výpočtu je proto pečlivý výběr referenčního systému, který bude použit k popisu pohybu..
Nakonec je třeba poznamenat, že inerciální referenční systémy nemusí nutně zůstat v klidu, jako například pozorovatel sledující vozidlo, jak otáčí křivkou. Inerciální referenční rámec, známý jako laboratorní referenční rámec, může to být také v pohybu. Samozřejmě s konstantní rychlostí vzhledem k setrvačné rychlosti.
Schéma volného těla v setrvačném a neinerciálním systému
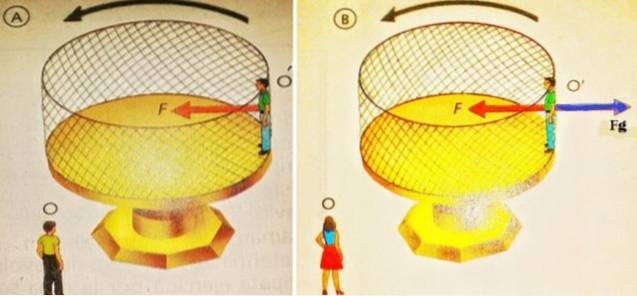
Na dalším obrázku vlevo stojí pozorovatel O a dívá se na O ', který je na plošině, která se otáčí naznačeným směrem. Pro O, což je setrvačný rám, jistě O 'stále rotuje kvůli dostředivé síle FC produkovaný stěnou mřížky na zadní straně O '.

Pouze v inerciálních referenčních rámcích platí druhý Newtonův zákon, který stanoví, že čistá síla se rovná součinu hmotnosti a zrychlení. Přitom se zobrazeným diagramem volného těla získáme:
FC = maC
FC= mvdva / R.
Podobně je na obrázku vpravo také diagram volného těla, který popisuje to, co vidí pozorovatel O '. Z jeho pohledu je v klidu, proto jsou jeho síly v rovnováze.
Tyto síly jsou: normální F, že zeď na ni působí červeně a směřuje ke středu a odstředivé síle FG která ji tlačí ven a která nevzniká žádnou interakcí, je neinerciální síla, která se objevuje v rotujících referenčních rámcích.
Odstředivá síla je fiktivní, je vyvážena skutečnou silou, kontaktní nebo normální silou, která směřuje ke středu. Proto:
∑FX = 0 → FG - F = 0
FG = F
Příklady
Přestože je odstředivá síla považována za pseudo sílu, její účinky jsou zcela reálné, jak je patrné z následujících příkladů:
- V každé točící se hře v zábavním parku je přítomna odstředivá síla. Zajišťuje, abychom „utekli z centra“ a nabízí neustálý odpor, pokud se pokusíte vstoupit do středu pohybujícího se kolotoče. V následujícím kyvadle vidíte odstředivou sílu:
- Coriolisův efekt vzniká rotací Země, díky čemuž Země přestala být setrvačným rámcem. Pak se objeví Coriolisova síla, což je pseudo-síla, která bočně odkloní objekty, stejně jako lidé, kteří se pokoušejí chodit po gramofonu..
Výcvik
Cvičení 1
Auto, které se točí s akcelerací NA napravo je vycpaná hračka visící z vnitřního zpětného zrcátka. Nakreslete a porovnejte diagramy volného těla hračky z pohledu:
a) Setrvačný referenční rám pozorovatele stojícího na silnici.
b) Cestující cestující v autě.
Řešení
Pozorovatel stojící na silnici si všimne, že se hračka pohybuje rychle a zrychluje NA doprava.
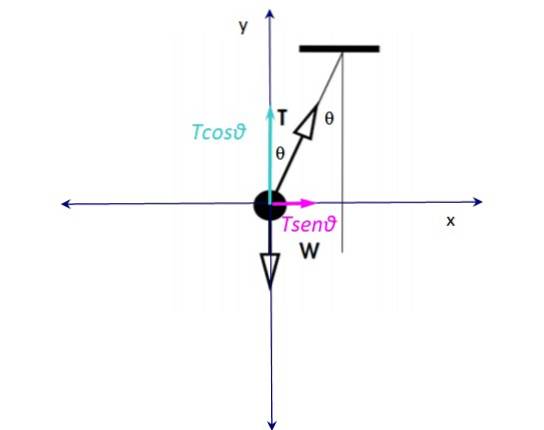
Na hračku působí dvě síly: na jedné straně napětí v provázku T a vertikální váha dolů Ž. Hmotnost je vyvážena svislou složkou napětí Tcosθ, Tím pádem:
W - Tcosθ = 0
Horizontální složka napětí: T. senθ je nevyvážená síla odpovědná za zrychlení doprava, proto dostředivá síla je:
FC= T. sinθ = maC
Řešení b
U cestujícího ve vozidle visí hračka v rovnováze a schéma je následující:

Stejně jako v předchozím případě je kompenzována hmotnost a svislá složka napětí. Horizontální složka je ale vyvážena fiktivní silou FG = mA, aby:
-mA + Tsenθ = 0
FG = mA
Cvičení 2
Mince je na okraji starého vinylového gramofonu, jehož poloměr je 15 cm a otáčí se rychlostí 33 otáček za minutu. Najděte minimální koeficient statického tření potřebný k tomu, aby mince zůstala na svém místě, pomocí referenčního rámce solidarity s mincí.
Řešení
Na obrázku je schéma volného těla pro pozorovatele pohybujícího se s mincí. Normální N že gramofon působí svisle nahoru, je vyváženo hmotností Ž, zatímco odstředivá síla FG je kompenzováno statickým třením Fdotek.
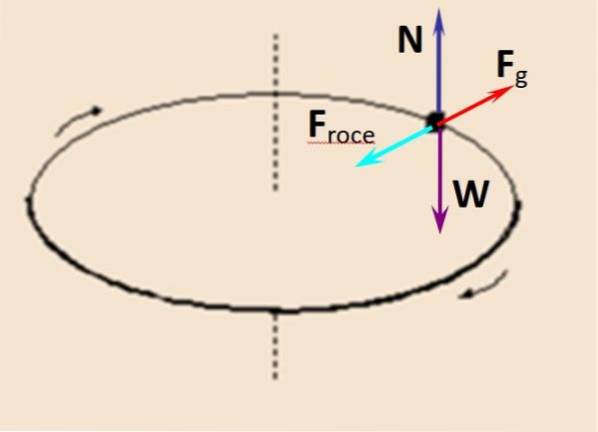
N - W = 0
Fdotek - FG = 0
Velikost odstředivé síly je mvdva/ R., jak bylo řečeno na začátku, pak:
Fdotek = FG = mvdva/ R.
Na druhou stranu je statická třecí síla dána vztahem:
Ftřít = μs.N
Kde μs je koeficient statického tření, bezrozměrná veličina, jejíž hodnota závisí na kontaktu povrchů. Dosazením této rovnice je:
μs.N = mvdva/ R → μs = mvdva/ R.N.
Zbývá určit velikost normálu, která souvisí s hmotností podle N = mg. Opětovné nahrazení:
μs = mvdva/R.mg → μs = vdva/ Rg
Zpět k prohlášení uvádí, že mince se otáčí rychlostí 33 otáček za minutu, což je úhlová rychlost nebo úhlová frekvence ω, vztahující se k lineární rychlosti proti:
v = ω.R = 33 ot / min. 2π radiány / rev. 15 cm. (1 min / 60 s) = 51,8 cm / s
μs = vdva/Rg=(51,8 cm / s)dva/ (15 cm x 981 cm / sdva) = 0,18
Výsledky tohoto cvičení by byly stejné, kdyby byl zvolen setrvačný referenční rámec. V tomto případě je jedinou silou schopnou způsobit zrychlení směrem ke středu statické tření..
Aplikace
Jak jsme řekli, odstředivá síla je fiktivní síla, která se neobjevuje v setrvačných rámcích, které jsou jediné, v nichž platí Newtonovy zákony. U nich je dostředivá síla zodpovědná za zajištění potřebného zrychlení těla směrem ke středu.
Dostředivá síla není jiná než již známá síla. Naopak právě tyto hrají v případě potřeby roli dostředivých sil. Například gravitace, která obíhá Měsíc kolem Země, napětí v laně, kterým se otáčí kámen, statické tření a elektrostatická síla.
Jelikož se však v praxi hojně vyskytují zrychlené referenční rámce, mají fiktivní síly velmi reálné účinky. Zde jsou například tři důležité aplikace, kde mají hmatatelné účinky:
Odstředivky
Odstředivky jsou nástroje široce používané v laboratoři. Cílem je, aby směs látek rotovala vysokou rychlostí a tyto látky s větší hmotou zažívaly větší odstředivou sílu, podle rovnice popsané na začátku..
Nejmohutnější částice pak budou mít tendenci vzdalovat se od osy otáčení, a budou tak odděleny od lehčích, které zůstanou blíže středu..
Pračky
Automatické pračky mají různé cykly odstřeďování. V nich je oblečení odstředěno, aby se odstranila zbývající voda. Čím více otáček cyklu, tím méně vlhké bude oblečení na konci praní.

Převýšení křivek
Auta jsou v zatáčkách na silnicích lepší, protože trať se mírně svažuje směrem ke středu zatáčky, která se označuje jako převýšení. Tímto způsobem vůz nezávisí výhradně na statickém tření mezi pneumatikami a vozovkou, aby dokončil zatáčku bez opuštění zatáčky..
Reference
- Acosta, Victor. Konstrukce didaktického průvodce o odstředivé síle pro studenty ve V cyklu 10. Citováno z: bdigital.unal.edu.co.
- Toppr. Zákony pohybu: kruhový pohyb. Obnoveno z: toppr.com.
- Resnick, R. (1999). Fyzický. Sv. 1. 3. vydání. Ve španělštině. Compañía Editorial Continental S.A. autor: C.V.
- Autonomní univerzita státu Hidalgo. Odstředivá síla. Obnoveno z: uaeh.edu.mx
- Wikipedia. Odstředivky. Obnoveno z: es.wikipedia.org.



Zatím žádné komentáře