
Analytická geometrie, jaké studie, historie, aplikace

The analytická geometrie studuje geometrické linie a obrazce pomocí základních technik algebry a matematické analýzy v daném souřadném systému.
Analytická geometrie je tedy odvětví matematiky, které podrobně analyzuje všechna data geometrických obrazců, tj. Mimo jiné objem, úhly, plochu, průsečíky, jejich vzdálenosti..
Základní charakteristikou analytické geometrie je, že umožňuje reprezentaci geometrických obrazců pomocí vzorců.
Například obvody jsou reprezentovány polynomiálními rovnicemi druhého stupně, zatímco čáry jsou vyjádřeny polynomiálními rovnicemi prvního stupně.
Analytická geometrie vzniká v sedmnáctém století kvůli potřebě odpovídat na problémy, které dosud neměly řešení. Jako vrcholní představitelé měli René Descartes a Pierre de Fermat.
Dnes na ni mnozí autoři poukazují jako na revoluční výtvor v dějinách matematiky, protože představuje počátek moderní matematiky.
Rejstřík článků
- 1 Historie analytické geometrie
- 1.1 Hlavní představitelé analytické geometrie
- 1.2 Pierre de Fermat
- 1.3 René Descartes
- 2 Základní prvky analytické geometrie
- 2.1 Kartézský souřadnicový systém
- 2.2 Obdélníkové souřadnicové systémy
- 2.3 Polární souřadnicový systém
- 2.4 Kartézská rovnice přímky
- 2.5 Přímka
- 2.6 Kuželosečky
- 2.7 Obvod
- 2.8 Podobenství
- 2.9 Elipsa
- 2.10 Hyperbola
- 3 Aplikace
- 3.1 Parabolická anténa
- 3.2 Visuté mosty
- 3.3 Astronomická analýza
- 3.4 dalekohled Cassegrain
- 4 Odkazy
Historie analytické geometrie
Termín analytická geometrie vznikl ve Francii v sedmnáctém století kvůli potřebě odpovědět na problémy, které nebylo možné vyřešit pomocí algebry a geometrie samostatně, ale řešení bylo v kombinovaném použití obou.
Hlavní představitelé analytické geometrie
Během sedmnáctého století dva Francouzi náhodou v životě provedli výzkum, který tak či onak skončil vytvořením analytické geometrie. Těmito lidmi byli Pierre de Fermat a René Descartes.
V současné době se má za to, že tvůrcem analytické geometrie byl René Descartes. Důvodem je skutečnost, že svou knihu vydal před Fermatem a také se do hloubky spolu s Descartem zabývá tématem analytické geometrie..
Fermat i Descartes však zjistili, že čáry a geometrické obrazce lze vyjádřit pomocí rovnic a rovnice lze vyjádřit jako přímky nebo geometrické obrazce..
Podle objevů těchto dvou lze říci, že oba jsou tvůrci analytické geometrie..
Pierre de Fermat
Pierre de Fermat byl francouzský matematik, který se narodil v roce 1601 a zemřel v roce 1665. Během svého života studoval geometrii Euklida, Apollónia a Pappuse, aby vyřešil problémy měření, které v té době existovaly.
Později tyto studie vyvolaly vytvoření geometrie. Nakonec byly vyjádřeny v jeho knize “Úvod do plochých a pevných míst“(Ad Locos Planos et Solidos Isagoge), který byl vydán 14 let po jeho smrti v roce 1679.
Pierre de Fermat v roce 1623 aplikoval analytickou geometrii na Apolloniusovy věty na geometrických místech. Byl také tím, kdo jako první použil analytickou geometrii v trojrozměrném prostoru..
René Descartes
Také známý jako Cartesius, byl matematik, fyzik a filozof, který se narodil 31. března 1596 ve Francii a zemřel v roce 1650..
René Descartes vydal v roce 1637 svou knihu „Pojednání o metodě správného vedení rozumu a hledání pravdy ve vědě"Známější jako"Metoda„A odtud byl světu představen pojem analytická geometrie. Jednou z jeho příloh byla „Geometrie“.
Základní prvky analytické geometrie
Analytická geometrie se skládá z následujících prvků:
Kartézský souřadnicový systém
Tento systém je pojmenován po Reném Descartesovi.
Nebyl to ten, kdo jej pojmenoval, ani ten, kdo dokončil kartézský souřadnicový systém, ale byl to ten, kdo hovořil o souřadnicích s kladnými čísly, což umožnilo budoucím vědcům jej dokončit..
Tento systém se skládá z pravoúhlého souřadnicového systému a polárního souřadného systému.
Obdélníkové souřadnicové systémy
Obdélníkové souřadnicové systémy se nazývají rovina tvořená obrysem dvou navzájem kolmých číselných linií, kde se hraniční bod shoduje se společnou nulou.
Pak by tento systém sestával z vodorovné čáry a vertikální..
Vodorovná čára je osa X nebo osa úsečky. Svislá čára by byla osa Y nebo osa souřadnice.
Polární souřadnicový systém
Tento systém má na starosti ověřování relativní polohy bodu ve vztahu k pevné linii a pevnému bodu na linii.
Kartézská rovnice přímky
Tato rovnice se získá z přímky, když jsou známy dva body, kterými prochází.
Přímka
Je to ten, který se neodchyluje, a proto nemá ani křivky, ani úhly.
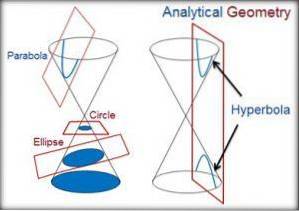
Kuželosečka
Jsou to křivky definované přímkami, které procházejí pevným bodem, a body křivky.
Elipsa, obvod, parabola a hyperbola jsou kuželovité křivky. Každá z nich je popsána níže.
Obvod
Obvod se nazývá křivka uzavřené roviny, která je tvořena všemi body roviny, které jsou ve stejné vzdálenosti od vnitřního bodu, tj. Od středu obvodu..
Podobenství
Jedná se o místo bodů v rovině, které jsou ve stejné vzdálenosti od pevného bodu (ohnisko) a pevné čáry (directrix). Potom je přímka a fokus tím, co definuje parabolu.
Parabola může být získána jako řez kuželovou rotační plochou rovinou rovnoběžnou s generatrixem.
Elipsa
Elipsa je uzavřená křivka, která popisuje bod při pohybu v rovině takovým způsobem, že součet jeho vzdáleností ke dvěma (2) pevným bodům (nazývaným ohniska) je konstantní.
Hyperbola
Křivka definovaná jako lokus bodů v rovině se nazývá hyperbola, pro kterou je rozdíl mezi vzdálenostmi dvou pevných bodů (ohnisek) konstantní..
Hyperbola má osu symetrie, která prochází ohniskem, která se nazývá ohnisková osa. Má také další, který je půlící částí segmentu, který má na svých koncích pevné body..
Aplikace
V různých oblastech každodenního života existují různé aplikace analytické geometrie. Například parabolu, jeden ze základních prvků analytické geometrie, můžeme najít v mnoha dnes používaných nástrojích. Některé z těchto nástrojů jsou následující:
Parabolická anténa
Parabolické antény mají reflektor generovaný jako výsledek paraboly, která se otáčí na ose uvedené antény. Povrch, který je generován v důsledku této akce, se nazývá paraboloid.
Tato schopnost paraboloidu se nazývá optická vlastnost nebo odrazová vlastnost paraboly a díky tomu je možné, aby paraboloid odrážel elektromagnetické vlny, které přijímá z napájecího mechanismu, který tvoří anténu..
Visuté mosty
Pokud lano unese hmotnost, která je homogenní, ale zároveň je podstatně větší než hmotnost samotného lana, výsledkem bude parabola.
Tento princip je zásadní pro konstrukci visutých mostů, které jsou obvykle podporovány širokými ocelovými lanovými konstrukcemi..
Princip paraboly v závěsných mostech byl použit v konstrukcích, jako je most Golden Gate, který se nachází ve městě San Francisco, ve Spojených státech, nebo Velký most v úžině Akashi, který se nachází v Japonsku a spojuje Ostrov Awaji s Honšú, hlavní ostrov této země.
Astronomická analýza
Analytická geometrie měla také velmi konkrétní a rozhodující využití v oblasti astronomie. V tomto případě je prvkem analytické geometrie, který zaujímá střed, elipsa; Jeho odrazem je zákon pohybu planet Johannesa Keplera.
Kepler, německý matematik a astronom, určil, že elipsa je křivka, která nejlépe odpovídá pohybu Marsu; Předtím vyzkoušel kruhový model navržený Copernicusem, ale uprostřed svých experimentů usoudil, že elipsa sloužila k nakreslení oběžné dráhy dokonale podobné oběžné dráze planety, kterou studoval..
Díky elipsě mohl Kepler potvrdit, že se planety pohybovaly po eliptických drahách; tato úvaha byla výrokem takzvaného druhého Keplerova zákona.
Z tohoto objevu, později obohateného anglickým fyzikem a matematikem Isaacem Newtonem, bylo možné studovat oběžné pohyby planet a rozšířit znalosti, které jsme měli o vesmíru, jehož jsme součástí.
Dalekohled Cassegrain
Dalekohled Cassegrain je pojmenován po svém vynálezci, francouzském fyzikovi Laurentovi Cassegrainovi. V tomto dalekohledu se používají principy analytické geometrie, protože se skládá hlavně ze dvou zrcadel: první je konkávní a parabolické a druhé se vyznačuje tím, že je konvexní a hyperbolické..
Umístění a povaha těchto zrcadel umožňují, aby nedocházelo k defektu známému jako sférická aberace; tato vada brání odrazu světelných paprsků v ohnisku dané čočky.
Dalekohled Cassegrain je velmi užitečný pro planetární pozorování a je také velmi univerzální a snadno použitelný..
Reference
- Analytická geometrie. Citováno dne 20. října 2017 z webu britannica.com
- Analytická geometrie. Citováno dne 20. října 2017 z encyclopediafmath.org
- Analytická geometrie. Citováno dne 20. října 2017 z khancademy.org
- Analytická geometrie. Citováno dne 20. října 2017 z wikipedia.org
- Analytická geometrie. Citováno dne 20. října 2017, z whitman.edu
- Analytická geometrie. Citováno dne 20. října 2017 z webu stewartcalculus.com
- Rovinová analytická geometrie Citováno dne 20. října 2017



Zatím žádné komentáře