The stupeň polynomu na A proměnná je dána termínem, který má největší exponent, a má-li polynom dvě nebo více proměnných, pak je stupeň určen součtem exponentů každého členu, přičemž větší součet je stupeň polynomu.
Podívejme se, jak určit stupeň polynomu praktickým způsobem.
Předpokládejme polynom P (x) = -5x + 8x3 + 7 - 4xdva. Tento polynom je jedna proměnná, v tomto případě jde o proměnnou X. Tento polynom se skládá z několika termínů, které jsou následující:
-5x; 8x3; 7; - 4xdva
Vyberme ze čtyř termínů ten, jehož exponent je větší, tento termín je:
8x3
A co je exponent? Odpověď je 3. Proto je P (x) polynom stupně 3.
Pokud dotyčný polynom má více než jednu proměnnou, pak stupeň může být:
-Absolutní
-Ve vztahu k proměnné
Absolutní stupeň se nachází, jak je vysvětleno na začátku: přidání exponentů každého termínu a výběr největšího.
Na druhou stranu je míra polynomu vzhledem k jedné z proměnných nebo písmen největší hodnotou exponenta, který dané písmeno má. Bod bude jasnější s příklady a vyřešenými cvičeními v následujících částech.
Rejstřík článků
Polynomy lze klasifikovat podle stupně a může to být první stupeň, druhý stupeň, třetí stupeň atd. U příkladu na obrázku 1 je energie monomiál prvního stupně pro hmotu.
Je také důležité si uvědomit, že počet výrazů, které má polynom, je stejný známka plus 1. A) Ano:
-Polynomy prvního stupně mají 2 termíny: a1x + anebo
-Polynom druhého stupně má 3 termíny: advaXdva + na1x + anebo
-Polynom třetího stupně má 4 termíny: a3X3 + nadvaXdva + na1x + anebo
A tak dále. Pozorný čtenář si všiml, že polynomy v předchozích příkladech jsou psány ve formě klesající, tj. uvedení termínu na první místo s Nejvyšší stupeň.
Následující tabulka ukazuje různé polynomy, a to jak jedné, tak několika proměnných a jejich příslušných absolutní stupně:
| Polynomiální | Školní známka |
|---|---|
| 3x4+5x3-2x + 3 | 4 |
| 7x3-2xdva+3x-6 | 3 |
| 6 | 0 |
| x-1 | 1 |
| X5-bx4+abx3+ab3Xdva | 6 |
| 3x3Y5 + 5xdvaY4 - 7xydva + 6 | 8 |
Poslední dva polynomy mají více než jednu proměnnou. Z nich byl výraz s nejvyšším absolutním stupněm zvýrazněn tučně, aby si čtenář mohl stupeň rychle zkontrolovat. Je důležité si uvědomit, že když proměnná nemá zapsaný exponent, rozumí se, že uvedený exponent se rovná 1.
Například v uvedeném termínu ab3Xdva existují tři proměnné, jmenovitě: na, b Y X. V tomto termínu, na se zvýší na 1, to znamená:
a = a1
Proto ab3Xdva = a1b3Xdva
Vzhledem k tomu, že exponent b je 3 a x je 2, okamžitě vyplývá, že stupeň tohoto termínu je:
1 + 3 + 2 = 6
Y je absolutní stupeň polynomu, protože žádný jiný člen nemá vyšší stupeň.
Při práci s polynomy je důležité věnovat pozornost stupni, protože nejprve a před provedením jakékoli operace je vhodné postupovat podle těchto kroků, ve kterých stupeň poskytuje velmi důležité informace:
-Seřaďte preferovaný polynom v sestupném směru. Tímto způsobem je termín s nejvyšším stupněm vlevo a termín s nejnižším stupněm vpravo..
-Redukovat jako termíny, postup, který spočívá v algebraickém přidání všech termínů stejné proměnné a stupně nalezených ve výrazu.
-Pokud je to nutné, jsou polynomy dokončeny a jsou vloženy termíny, jejichž koeficient je 0, v případě, že chybí termíny s nějakým exponentem.
Vzhledem k polynomu P (x) = 6xdva - 5x4- 2x + 3x + 7 + 2x5 - 3x3 + X7 -12 je žádáno, aby jej objednal v sestupném pořadí, omezil podobné podmínky, pokud existují, a doplnil chybějící podmínky, pokud je to nutné.
První věc, kterou je třeba hledat, je termín s největším exponentem, kterým je stupeň polynomu, který se ukáže být:
X7
Proto P (x) je stupně 7. Dále je uspořádán polynom, počínaje tímto výrazem vlevo:
P (x) = x7 + 2x5 - 5x4 - 3x3 + 6xdva - 2x + 3x + 7-12
Nyní jsou redukovány podobné výrazy, které jsou následující: - 2x a 3x na jedné straně. A 7 a -12 na druhé straně. Abychom je snížili, koeficienty se přidají algebraicky a proměnná zůstane beze změny (pokud se proměnná nezobrazí vedle koeficientu, nezapomeňte, že x0 = 1):
-2x + 3x = x
7-12 = -5
Nahraďte tyto výsledky v P (x):
P (x) = x7 +2x5 - 5x4 - 3x3 + 6xdva + x -5
A nakonec se polynom zkoumá, aby se zjistilo, zda chybí nějaký exponent, a skutečně chybí termín, jehož exponent je 6, proto je doplněn nulami jako je tento:
P (x) = x7 + 0x6 +2x5 - 5x4 - 3x3 + 6xdva + x - 5
Nyní je pozorováno, že na polynomu bylo ponecháno 8 členů, protože jak již bylo řečeno, počet členů se rovná stupni + 1.
S polynomy můžete provádět operace sčítání a odčítání, při kterých se sčítají nebo odečítají pouze podobné výrazy, tedy ty, které mají stejnou proměnnou a stejný stupeň. Pokud neexistují žádné podobné výrazy, je jednoduše uvedeno sčítání nebo odčítání.
Jakmile je sčítání nebo odčítání provedeno, přičemž druhý je součtem opaku, je stupeň výsledného polynomu vždy stejný nebo menší než stupeň polynomu, který přidává nejvyšší stupeň.
Najděte následující součet a určete jeho absolutní stupeň:
na3- 8axdva + X3 + 5dvax - 6axdva - X3 + 3. místo3 - 5dvax - x3 + na3+ 14axdva - X3
Jedná se o polynom se dvěma proměnnými, takže je vhodné redukovat podobné výrazy:
na3- 8axdva + X3 + 5dvax - 6axdva - X3 + 3. místo3 - 5dvax - x3 + na3+ 14axdva - X3 =
= a3 + 3. místo3 + na3 - 8axdva - 6axdva+ 14axdva +5dvax - 5dvax + x3- X3- X3- X3 =
= 5a3 - 2x3
Oba termíny mají stupeň 3 v každé proměnné. Proto je absolutní stupeň polynomu 3.
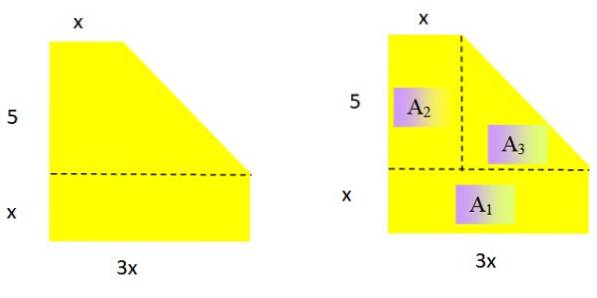
Vyjádřete oblast následujícího rovinného geometrického útvaru jako polynom (obrázek 2 vlevo). Jaký je stupeň výsledného polynomu?
Jelikož jde o oblast, výsledný polynom musí být v proměnné x stupně 2. Chcete-li určit vhodný výraz pro danou oblast, rozloží se obrázek na známé oblasti:
Plocha obdélníku a trojúhelníku jsou příslušně: základna x výška Y základna x výška / 2
NA1 = x. 3x = 3xdva; NAdva = 5. x = 5x; NA3 = 5. (2x / 2) = 5x
Poznámka: základna trojúhelníku je 3x - x = 2x a jeho výška je 5.
Nyní jsou sečteny tři získané výrazy, s tím máme plochu obrázku jako funkci X:
3xdva + 5x + 5x = 3xdva + 10x
Zatím žádné komentáře