
Ampereův zákon a rovnice, důkaz, cvičení
The Ampereův zákon uvádí, že oběh magnetického indukčního vektoru B je úměrná intenzitě I proudu protékajícího tímto proudem.
Na druhé straně oběh B je součet všech produktů mezi tangenciální složkou B║ a délka malého segmentu Δℓ uzavřené křivky C, kolem okruhu. Matematicky je to napsáno takto:
∑ B║ .Δℓ ∝ Já
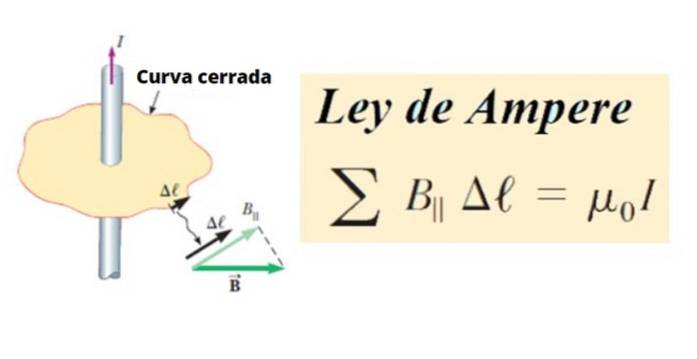
Stejně jako libovolná přímka nebo křivka C jej lze rozdělit na malé segmenty Δℓ, a ty zase mohou být nekonečně malé, pak se jim říká dℓ.
V tomto případě se součet stane liniovým integrálem skalárního součinu mezi vektory B ads. Uvedený produkt obsahuje tangenciální složku B, kterou je B cosθ, kde θ je úhel mezi vektory:
Malý kruh procházející integrálem znamená, že integrace probíhá přes uzavřenou cestu C, což v tomto případě zahrnuje proud protékající průřezem vodiče.
Konstanta proporcionality nezbytná k nastolení rovnosti je μnebo, propustnost vakua. Tímto způsobem Ampereův zákon zní:

Ampereův zákon nám říká, že přímka je integrální ∫C B ∙ ds je přesně μneboJá, ale neposkytuje nám podrobnosti o tom, jak je magnetické pole orientováno B s ohledem na křivku C v každém bodě, ani na to, jak vypočítat integrál. Pouze nám říká, že výsledek je vždy μneboJá.
Rejstřík článků
- 1 Důkaz Ampereova zákona
- 1.1 Magnetické pole přímočarého a nekonečného drátu
- 2 Vyřešená cvičení
- 2.1 - Cvičení 1
- 2.2 - Cvičení 2
- 3 Odkazy
Demonstrace Ampereova zákona
Ampereův zákon je ověřen experimentálně kontrolou magnetického pole vytvářeného velmi dlouhým přímým vodičem. Před řešením problému musíme zdůraznit dva případy zvláštního zájmu v předchozí rovnici:
-První je kdy B ads jsou paralelní, což znamená, že B je tangenciální vůči C. Pak je úhel mezi oběma vektory 0 ° a skalární součin je jednoduše součinem velikostí B.ds.
-Druhý nastane, pokud B ads jsou kolmé, v takovém případě je skalární součin 0, protože úhel mezi vektory je 90 °, jehož kosinus je 0.
Dalším důležitým detailem je volba křivky C, na které se vyhodnocuje cirkulace pole. Ampereův zákon neurčuje, co to může být, ale musí zahrnovat současnou distribuci. Rovněž neříká, kterým směrem se má křivka pohybovat, a existují dvě možnosti.
Řešením je přiřadit znaménka podle pravidla pravého palce. Čtyři prsty jsou zakřivené ve směru, ve kterém se chcete integrovat, obvykle to bude stejné jako pole B obíhat. Pokud aktuální ukazuje ve směru pravého palce, je mu přiřazeno znaménko + a pokud ne, znaménko -.
To platí, pokud existuje distribuce s několika proudy, některé mohou být kladné a jiné negativní. Algebraický součet z nich je ten, který umístíme do Ampereho zákona, který se obvykle nazývá proud uzamčen (křivkou C).
Nekonečné přímé magnetické pole drátu
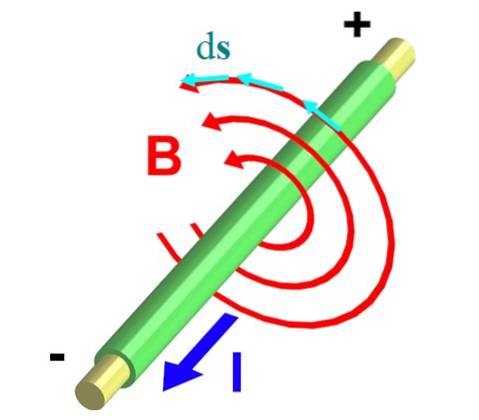
Obrázek 2 ukazuje vodič nesoucí proud I mimo rovinu. Pravidlo pravého palce to zajišťuje B cirkuluje proti směru hodinových ručiček, což popisuje obvody, jak je znázorněno červenými šipkami.

Vezměme si jeden z nich, jehož poloměr je r. Rozdělíme to na malé diferenciální segmenty ds, reprezentované vektory v modré barvě. Oba vektory, B ads, jsou rovnoběžné v každém bodě na obvodu, a tedy integrál ∫C B ∙ ds Transformuje se do:
∫C BDS
Je to proto, jak jsme již řekli, tečkovaný produkt B ∙ ds je součin velikostí vektorů kosinusem 0 °. Výsledek integrálu známe díky Ampèrovu zákonu, proto píšeme:
∫C Bds = μneboJá
Protože velikost pole je konstantní po celé trajektorii, opouští integrál:
B ∫C ds = μneboJá
Integrál ∫C ds představuje součet všech nekonečně malých segmentů, které tvoří obvod poloměru r, ekvivalent jeho délky, součin jeho poloměru o 2π:
B.2πr = μneboJá
A odtud zjistíme, že velikost B je:
B = μneboI / 2πr
Je třeba zdůraznit, že i když je zvolená cesta (nebo ampereiánský obvod) nebyl kruhový, výsledek integrálu zůstává μneboJá však ∫C B ∙ ds už by to nebylo B.2πr.
Užitečnost Ampèrova zákona pro určení magnetického pole proto spočívá ve volbě distribucí s vysokou symetrií, takže integrál lze snadno vyhodnotit. Kruhové a přímočaré cesty tento požadavek splňují.
Vyřešená cvičení
- Cvičení 1
Zvažte křivky a, b, c a d zobrazené na obrázku 3. Zahrnují tři proudy, dva opouštějící rovinu, symbolizované bodem ( . ), jehož intenzity jsou 1 A a 5 A, a proud, který vstupuje do roviny, který je označen křížkem a jehož velikost je 2 A.
Najděte aktuální uzavřený každou křivkou.
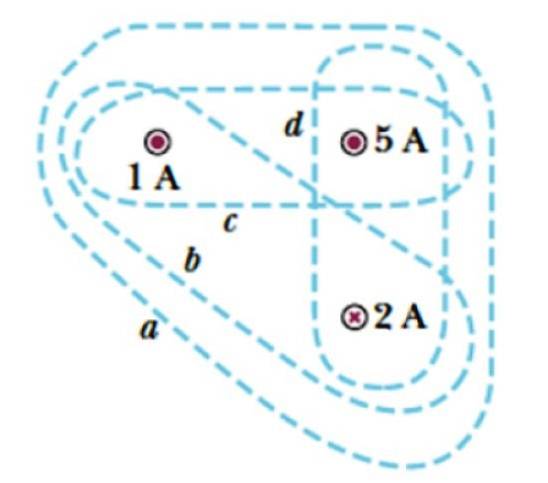
Řešení
Proudům vycházejícím z papíru je přiřazeno znaménko +. Podle tohoto:
Křivka a
Zahrnuje tři proudy, proto je uzavřený proud + 1 A + 5 A - 2 A = 4 A.
Křivka b
V této křivce jsou pouze proudy 1 A a - 2 A, proto je uzavřený proud - 2 A.
Křivka c
Uzavírá odchozí proudy 1A a 5 A, proto je proud uzamčen 6 A.
Zakřivený
Proudy uvnitř jsou +5 A a - 2 A, takže obsahuje síťový proud 3 A.
- Cvičení 2
Vypočítejte velikost magnetického pole vytvářeného velmi dlouhým přímým vodičem v bodě vzdáleném 1 metr od něj, pokud vodič vede proud 1 A.
Řešení
Podle Ampereova zákona je pole drátu dáno:
B = μneboI / 2πr = (4π x 10-7 x 1 / 2π x 1) T = 2 x 10-7 T.
Reference
- Figueroa, D. (2005). Série: Fyzika pro vědu a techniku. Svazek 6. Elektromagnetismus. Upravil Douglas Figueroa (USB).
- Knight, R. 2017. Fyzika pro vědce a inženýrství: strategický přístup. Pearson.
- Sears, Zemansky. 2016. Univerzitní fyzika s moderní fyzikou. 14. Vydání Volume 2.
- Serway, R. 2009. College Physics. Cengage Learning.
- Tipler, P. (2006) Fyzika pro vědu a technologii. 5. vydání, svazek 2. Redakční reverté.


Zatím žádné komentáře