Gaussův zákon

Co je Gaussův zákon?

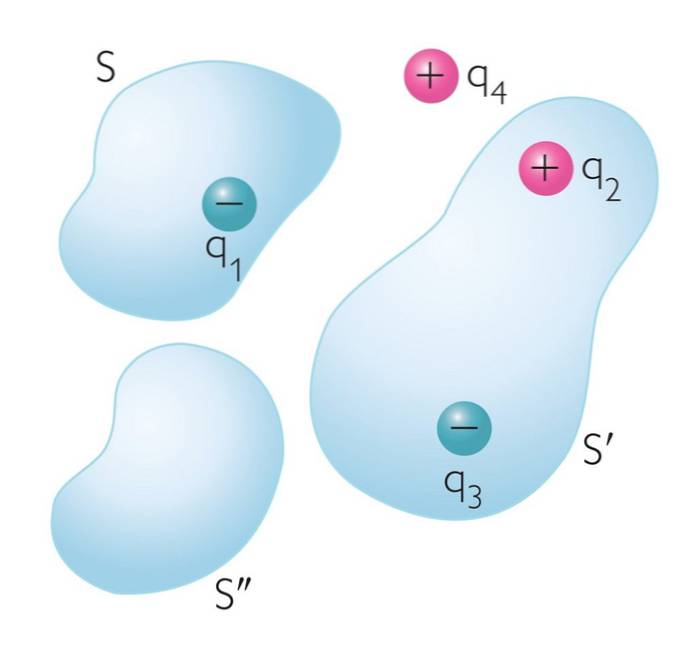
The Gaussův zákon stanoví, že tok elektrického pole imaginárním uzavřeným povrchem je úměrný hodnotě čistého náboje částic nalezených uvnitř uvedeného povrchu.

Označujeme elektrický tok uzavřeným povrchem jako Φ_A a síťový náboj uzavřený povrchem Q_příloha, pak se vytvoří následující matematický vztah:

Φ_A = c ∙ Q_příloha

Kde C je konstanta proporcionality.

Vysvětlení Gaussova zákona

Abychom pochopili význam Gaussova zákona, je nutné vysvětlit pojmy obsažené v jeho tvrzení: elektrický náboj, elektrické pole a tok elektrického pole povrchem..

Elektrický náboj

Elektrický náboj je jednou ze základních vlastností hmoty. Nabitý objekt může mít jeden ze dvou typů náboje: kladný nebo záporný, i když jsou objekty obvykle neutrální, to znamená, že mají stejné množství záporného náboje jako kladný..

Dva nabité objekty stejného typu se navzájem odpuzují, i když mezi nimi nedochází ke kontaktu a jsou ve vakuu. Naopak, když každé z těl má náboje jiného znamení, přitahují se navzájem. Tento typ interakce na dálku je známý jako elektrická interakce..

V mezinárodním systému jednotek SI se elektrický náboj měří v coulombs (C). Negativním nosičem elementárního náboje je elektron s nákladem -1,6 x 10^-19C a kladným nosičem elementárního náboje je proton s hodnotou náboje +1,6 x 10^-19C. Typicky nabité subjekty mají mezi 10^-9C Y 10^-3C.

elektrické pole

Elektricky nabité tělo mění prostor ve svém prostředí a plní ho něčím neviditelným, které se říká elektrické pole. Vědět, že toto pole je přítomno, vyžaduje kladný testovací náboj.

Pokud je zkušební náboj umístěn na místě, kde je elektrické pole, objeví se na něj síla v určitém směru, který je stejný jako v elektrickém poli. Intenzita pole je síla na testovací náboj dělená množstvím náboje na testovacím náboji. Pak jednotky elektrického pole A v mezinárodním systému jednotek jsou Newton Pojď dovnitř coulomb: [E] = N / C.

Poplatky kladného bodu vytvářejí radiální pole směrem ven, zatímco záporné náboje vytvářejí radiálně směrem dovnitř pole. Kromě toho se pole produkované bodovým nábojem rozpadá s inverzí druhé mocniny vzdálenosti k uvedenému náboji.

Elektrické siločáry

Michael Faraday (1791 - 1867) byl první, kdo měl mentální obraz elektrického pole a představoval si ho jako čáry, které sledují směr pole. V případě kladného bodového náboje jsou tyto čáry radiální a začínají od středu ven. Tam, kde jsou čáry blíže k sobě, je pole intenzivnější a méně intenzivní tam, kde jsou dále od sebe.

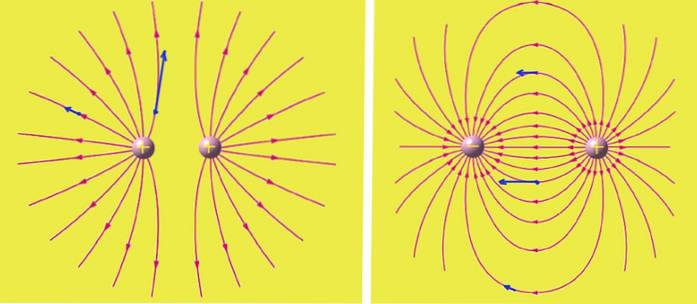
Kladné náboje jsou zdroje, ze kterých vycházejí čáry elektrického pole, zatímco záporné náboje jsou výlevky čar..

Elektrické siločáry se do sebe neuzavírají. V sadě nábojů čáry opouštějí kladné náboje a vstupují do kladných, ale mohou také dosáhnout nebo pocházet z nekonečna.

Rovněž se neprotínají a v každém bodě vesmíru je vektor elektrického pole tečný k polní čáře a úměrný hustotě čar tam..

Tok elektrického pole

Čáry elektrického pole se podobají proudnicím mírně tekoucí řeky, proto se zrodila koncepce toku elektrického pole..

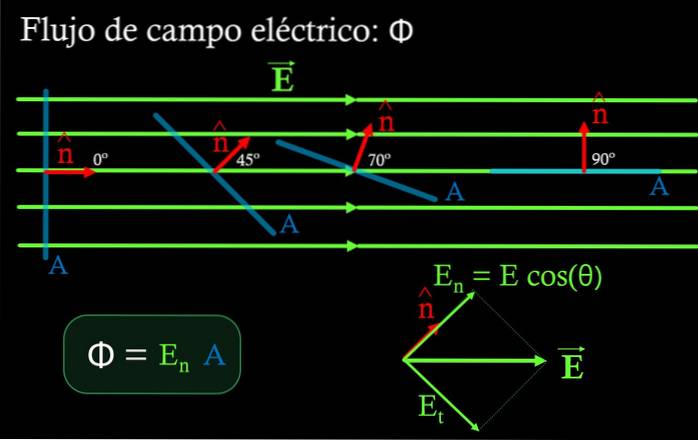
V oblasti, kde je elektrické pole rovnoměrné, je tok Φ přes rovný povrch produktem normální složky pole E_n na tento povrch, vynásobený plochou NA Ze stejného:

Φ = E_n ∙ A

Složka E_n se získá vynásobením velikosti elektrického pole kosinem úhlu vytvořeného mezi polem a jednotkovým normálovým vektorem k ploše NA. (viz obrázek 4).

Gaussovy právní aplikace

Gaussův zákon lze použít k určení elektrického pole produkovaného distribucí nábojů s vysokým stupněm symetrie.

Elektrické pole bodového náboje

Bodový náboj vytváří radiální elektrické pole, které je odchozí, pokud je náboj kladný a jinak přichází..

Zvolíme-li jako Gaussovu plochu imaginární sféru o poloměru R a soustřednou k náboji Q, bude mít elektrické pole ve všech bodech na povrchu uvedené koule stejnou velikost a jeho směr je vždy kolmý k povrchu. Takže v tomto případě je tok elektrického pole produktem velikosti pole a celkové plochy sférického povrchu:

Φ = E ∙ A = E ∙ 4πR^dva

Na druhou stranu Gaussův zákon říká, že: Φ = c ∙ Q, což je konstanta proporcionality C. Při práci v jednotkách mezinárodního měřicího systému konstanta C je inverzní k permitivitě vakua a Gaussův zákon je formulován takto:

Φ = (1 / ε_nebo) ∙ Q

Začleněním výsledku získaného pro tok ke Gaussovu zákonu máme:

E ∙ 4πR^dva = (1 / ε_nebo) ∙ Q

A pro velikost A výsledek:

E = (1 / 4πε_nebo) ∙ (Q / R^dva)

Což plně souhlasí s Coulombovým zákonem elektrického pole bodového náboje.

Výcvik

Cvičení 1

Dva bodové náboje leží libovolně uvnitř Gaussova povrchu S. O jednom z nich je známo, že mají hodnotu +3 nC (3 nano-coulomb). Pokud je tok čistého elektrického pole Gaussovým povrchem 113 (N / C) m^dva, Jaká bude hodnota druhého zatížení?

Řešení

Gaussův zákon to říká

Φ_A = (1 / ε_nebo) ∙ Q_příloha

Čistý uzavřený poplatek je tedy:

Q_příloha = Φ_A ∙ ε_nebo

Nahrazení výsledků dat:

Q_příloha = 113 (N / C) m^dva ∙ 8,85 x 10^-12 (C^dva m^-dva N^-1) = 1 x 10^-9 C = 1 nC.

Ale Q_příloha = + Q - q, kde kladný náboj má známou hodnotu +3 nC, bude tedy náboj nutně -2 nC.

Cvičení 2

Na obrázku 2 je uspořádání (vlevo) dvou kladných nábojů, každý s hodnotou + q a další uspořádání (vpravo) s nábojem + q a druhý -q. Každé uspořádání je uzavřeno v imaginární krabičce se všemi svými 10 cm okraji. Pokud | q | = 3 μC, najděte čistý tok elektrického pole skrz krabici pro každé uspořádání.

Řešení

V prvním uspořádání je čistý tok:

Φ_A = (1 / ε_nebo) ∙ (+ q + q) = 678000 (N / C) m^dva

V uspořádání vpravo je čistý tok pomyslným rámečkem obsahujícím dvojici nábojů nulový..

Reference

1. Cosenza, M. Elektromagnetismus. Univerzita v Andách.
2. Díaz, R. Elektrodynamika: poznámky třídy. Kolumbijská národní univerzita.
3. Figueroa, D. (2005). Série: Fyzika pro vědu a techniku. Svazek 6. Elektromagnetismus. Upravil Douglas Figueroa (USB).
4. Jackson, J. D. Classical Electrodynamics. 3. místo Ed. Wiley.
5. Tarazona, C. Úvod do elektrodynamiky. Redakční univerzita Manuela Beltrán.