The zákon o ideálním plynu je stavová rovnice, která popisuje vztah mezi stavovými funkcemi spojenými s ideálním plynem; jako je teplota, tlak, objem a počet krtků. Tento zákon umožňuje studovat skutečné plynné systémy jejich porovnáním s idealizovanými verzemi..
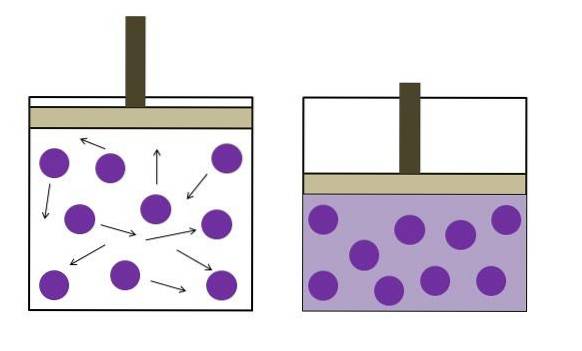
Ideálním plynem je teoretický plyn složený z bodových nebo sférických částic, které se náhodně pohybují; s velkou kinetickou energií, kde jedinou interakcí mezi nimi jsou zcela pružné rázy. Kromě toho dodržují zákon o ideálním plynu.
Při standardním tlaku a teplotě (STP): 1 atm tlaku a teplotě 0 ° C se většina skutečných plynů chová kvalitativně jako ideální plyny; pokud jsou jejich hustoty nízké. Velké mezimolekulární nebo interatomové vzdálenosti (pro vzácné plyny) takové aproximace usnadňují..
Za podmínek STP se kyslík, dusík, vodík, ušlechtilé plyny a některé plyny ve formě sloučenin, jako je oxid uhličitý, chovají jako ideální plyn..
Model ideálního plynu má tendenci selhat při nízkých teplotách, vysokých tlacích a vysokých hustotách částic; když se stávají důležité mezimolekulární interakce, stejně jako velikost částic.
Zákon o ideálním plynu je složen ze tří zákonů o plynu: Boyleova a Mariottova zákona, Charlesova a Gay-Lusscova zákona a Avogadrova zákona..
Rejstřík článků
Zákon o plynu je matematicky vyjádřen vzorcem:
PV = nRT
Kde P je tlak vyvíjený plynem. Obvykle se vyjadřuje jednotkou atmosféry (atm), i když lze vyjádřit i v jiných jednotkách: mmHg, pascal, bar atd..
Objem V obsazený plynem je obvykle vyjádřen v jednotkách litru (L). Zatímco n je počet molů, R univerzální plynová konstanta a T teplota vyjádřená v Kelvinech (K).
Nejpoužívanější výraz v plynech pro R se rovná 0,08206 L atm K-1Krtek-1. Ačkoli jednotka SI pro plynovou konstantu má hodnotu 8,3145 J mol-1K.-1. Obě jsou platné, pokud je věnována pozornost jednotkám ostatních proměnných (P, T a V).
Zákon o ideálním plynu je kombinací zákona Boylea-Mariotta, zákona Charlese-Gaye-Lussaca a zákona Avogadra.
Nezávisle jej formulovali fyzik Robert Boyle (1662) a fyzik a botanik Edme Mariotte (1676). Zákon je stanoven následovně: při konstantní teplotě je objem stálé hmotnosti plynu nepřímo úměrný tlaku, který vyvíjí.
PV ∝ k
Pomocí dvojtečky:
P1PROTI1 = PdvaPROTIdva
Zákon publikoval Gay-Lussac v roce 1803, odkazoval však na nepublikované dílo Jacquese Charlese (1787). Z tohoto důvodu je zákon znám jako Charlesův zákon..
Zákon stanoví, že při konstantním tlaku existuje přímý proporcionální vztah mezi objemem obsazeným plynem a jeho teplotou.
V ∝ kdvaT
Pomocí dvojtečky:
PROTI1/ T1 = Vdva/ Tdva
PROTI1Tdva = VdvaT1
Zákon vyhlásil Amadeo Avogadro v roce 1811 a poukázal na to, že stejné objemy všech plynů při stejném tlaku a teplotě mají stejný počet molekul.
PROTI1/ n1 = Vdva/ ndva
Zákon ideálního plynu stanoví vztah mezi čtyřmi nezávislými fyzikálními vlastnostmi plynu: tlakem, objemem, teplotou a množstvím plynu. Stačí znát hodnotu tří z nich, abychom mohli získat hodnotu zbývajících.
Zákon stanoví podmínky, které určují, kdy se plyn chová ideálně a kdy se od tohoto chování vzdaluje.
Například takzvaný kompresní faktor (PV / nRT) má pro ideální plyny hodnotu 1. Odchylka od hodnoty 1 pro kompresní faktor naznačuje, že chování plynu je daleko od chování, které ukazuje ideální plyn.
Proto by došlo k chybě při aplikaci rovnice ideálního plynu na plyn, který se nechová podle modelu.
Rovnici zákona ideálního plynu lze použít k výpočtu hustoty plynu a jeho molární hmotnosti. Jednoduchou modifikací lze nalézt matematický výraz, který souvisí s hustotou (d) plynu a jeho molární hmotou (M):
d = MP / RT
A čištění M:
M = dRT / P
Stechiometrie je odvětví chemie, které se týká množství každého z reaktantů přítomných v produktech, které se účastní chemické reakce, obecně vyjádřeno v molech..
Použití rovnice ideálního plynu umožňuje stanovení objemu plynu produkovaného chemickou reakcí; protože počet molů lze získat chemickou reakcí. Poté lze vypočítat objem plynu:
PV = nRT
V = nRT / P
Měřením V lze určit výtěžek nebo postup uvedené reakce. Pokud již nejsou žádné plyny, znamená to, že činidla jsou zcela vyčerpána.
Zákon ideálního plynu lze použít společně s Daltonovým zákonem o parciálním tlaku k výpočtu parciálních tlaků různých plynů přítomných ve směsi plynů..
Vztah platí:
P = nRT / V
Zjistit tlak každého z plynů přítomných ve směsi.
Provádí se reakce, při které se vytváří plyn, který se shromažďuje pomocí experimentálního návrhu ve vodě. Celkový tlak plynu plus tlak vodní páry je známý. Jeho hodnotu lze získat v tabulce a odečtením tlaku plynu lze vypočítat.
Ze stechiometrie chemické reakce lze získat počet molů plynu a použít vztah:
V = nRT / P
Vypočítá se objem vyrobeného plynu.
Plyn má hustotu 0,0847 g / l při 17 ° C a tlak 760 torr. Jaká je jeho molární hmotnost? Co je to plyn?
Vycházíme z rovnice
M = dRT / P
Nejprve převedeme jednotky teploty na kelvin:
T = 17 ° C + 273,15 K = 290,15 K.
A tlak 760 torr odpovídá tlaku 1 atm. Nyní musíte pouze nahradit hodnoty a vyřešit:
M = (0,0847 g / l) (0,08206 l atm K.-1Krtek-1) (290,15 K) / 1 atm
M = 2,016 g / mol
Tato molární hmotnost může odpovídat jedinému druhu: rozsivkové molekule vodíku, Hdva.
Hmotnost 0,00553 g rtuti (Hg) v plynné fázi se nachází v objemu 520 litrů a při teplotě 507 K. Vypočítejte tlak vyvíjený pomocí Hg. Molární hmotnost Hg je 200,59 g / mol.
Problém je vyřešen pomocí rovnice:
PV = nRT
Informace o počtu molů Hg se nezobrazí; ale lze je získat použitím jejich molární hmotnosti:
Počet mol Hg = (0,00553 g Hg) (1 mol Hg / 200,59 g)
= 2757 10-5 krtci
Nyní musíme vyřešit P a nahradit hodnoty:
P = nRT / V
= (2757 10-5 krtci) (8,20610-dva L atm K.-1Krtek-1) (507 K) / 520 l
= 2,2 10-6 bankomat
Vypočítejte tlak generovaný kyselinou chlorovodíkovou produkovanou reakcí 4,8 g plynného chloru (Cldva) s plynným vodíkem (Hdva), v objemu 5,25 L a při teplotě 310 K. Molární hmotnost Cldva je 70,9 g / mol.
H2 g) + Cl2 g) → 2 HCl(G)
Problém je vyřešen pomocí rovnice ideálního plynu. Ale množství HCl je vyjádřeno v gramech a ne v molech, takže je provedena správná transformace.
Mole HCl = (4,8 g Cldva) (1 mol Cldva/ 70,9 g Cldva) (2 mol HCl / 1 mol Cl.)dva)
= 0,135 mol HC1
Uplatnění rovnice zákona o ideálním plynu:
PV = nRT
P = nRT / V
= (0,135 mol HCl) (0,08206 l atm K.-1Krtek-1) (310 K) / 5,25 l
= 0,65 atm
Vzorek 0,130 g plynné sloučeniny zaujímá při teplotě 70 ° C a tlaku 720 torr objem 140 ml. Jaká je jeho molární hmotnost?
Chcete-li použít rovnici ideálního plynu, je třeba nejprve provést několik změn:
V = (140 ml) (1 l / 1000 ml)
= 0,14 litru
Když vezmeme objem v litrech, musíme nyní vyjádřit teplotu v kelvinech:
T = 70 ° C + 273,15 K = 243,15 K
A nakonec musíme převést tlak v jednotkách atmosféry:
P = (720 torr) (1 atm / 760 torr)
= 0,947 atm
Prvním krokem při řešení problému je získání počtu molů sloučeniny. K tomu se používá rovnice ideálního plynu, kterou vyřešíme pro n:
PV = nRT
n = PV / RT
= (0,947 atm) (0,14 l) / (0,08206 l atm K.-1Krtek-1) (243,15 K)
= 0,067 mol
Musíte pouze vypočítat molární hmotnost dělením gramů získanými moly:
Molární hmotnost = gramy sloučeniny / počet molů.
= 0,130 g / 0,067 mol
= 19,49 g / mol
Zatím žádné komentáře