Blokové algebrické prvky, příklady, řešená cvičení

The bloková algebra odkazuje na sadu operací, které jsou prováděny prostřednictvím bloků. Tyto a některé další prvky slouží k schematickému znázornění systému a snadné vizualizaci jeho odezvy na daný vstup..

Obecně platí, že systém obsahuje různé elektrické, elektronické a elektromechanické prvky a každý z nich, s příslušnou funkcí a polohou v systému, jakož i způsobem, jakým spolu souvisejí, je načrtnut funkčními bloky.

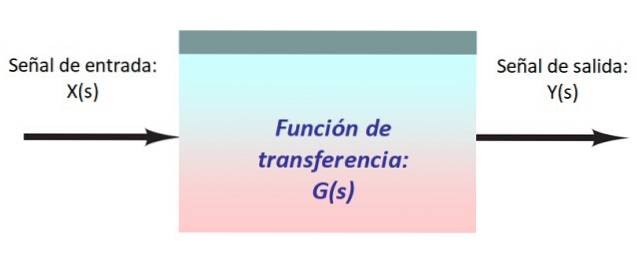
Na obrázku výše je velmi jednoduchý systém, který se skládá ze vstupního signálu X (s), který vstupuje do bloku s přenosovou funkcí G (s), která jej upravuje a vytváří výstup Y (y).

Je vhodné reprezentovat signály a jejich cestu systémem pomocí šipek, které vstupují a opouštějí každý blok. Tok signálu je obvykle směrován zleva doprava.

Výhodou tohoto druhu schématu je vizuální pomůcka, která poskytuje porozumění systému, i když nejde o fyzickou reprezentaci systému. Blokové schéma ve skutečnosti není jedinečné, protože v závislosti na úhlu pohledu lze dokonce nakreslit několik diagramů stejného systému..

Může se také stát, že stejný diagram slouží několika systémům, které spolu nemusí nutně souviset, pokud dostatečně popisuje jejich chování. Existují různé systémy, jejichž odezva je v mnoha ohledech podobná, například LC obvod (induktor-kondenzátor) a systém s hmotnou pružinou..

Rejstřík článků

• 1 Co je to blokové schéma?
• 2 Prvky blokového diagramu
  • 2.1 Signál
  • 2.2 Blok
  • 2.3 Součet bodů
  • 2.4 Bod odbočky
• 3 Příklady pravidel blokové algebry
  • 3.1 Kaskádové bloky
  • 3.2 Bloky paralelně
  • 3.3 Přesuňte zmije doleva
  • 3.4 Přesuňte zmije doprava
  • 3.5 Posun větvícího bodu zleva doprava
  • 3.6 Posuňte bod větvení zprava doleva
  • 3.7 Systém zpětné vazby
  • 3.8 Systém se zpětnou vazbou a převodníkem
• 4 Vyřešená cvičení
  • 4.1 Cvičení 1
  • 4.2 Cvičení 2
• 5 Reference

Co je to blokové schéma?

Systémy jsou obecně komplikovanější než na obrázku 1, ale bloková algebra poskytuje řadu jednoduchých pravidel pro manipulaci se systémovým schématem a jeho redukci na nejjednodušší verzi..

Jak bylo vysvětleno na začátku, diagram používá bloky, šipky a kruhy k navázání vztahu mezi každou komponentou systému a tokem signálů, které jím procházejí..

Bloková algebra vám umožňuje porovnat dva nebo více signálů jejich přidáním, odečtením a vynásobením a také analýzou příspěvku jednotlivých komponent do systému..

Díky tomu je možné redukovat celý systém na jediný vstupní signál, jedinou přenosovou funkci, která plně popisuje činnost systému a odpovídající výstup..

Prvky blokového diagramu

Prvky blokového diagramu jsou následující:

Signál

Signály jsou velmi rozmanité povahy, například je běžné, že jde o elektrický proud nebo napětí, ale může to být světlo, zvuk a další. Důležité je, že obsahuje informace o určitém systému.

Signál je označen velkým písmenem, pokud je funkcí proměnné s Laplaceovy transformace: X (s) (viz obrázek 1) nebo s malými písmeny, pokud je to funkce času t, jako x (t).

V blokovém diagramu je vstupní signál reprezentován šipkou směřující k bloku, zatímco výstupní signál, označený jako Y (s) nebo y (t), je označen odchozí šipkou.

Vstupní i výstupní signály jsou jedinečné a směr toku informací je určen směrem šipky. A algebra je stejná pro každou ze dvou proměnných.

Blok

Blok je reprezentován čtvercem nebo obdélníkem (viz obrázek 1) a lze jej použít k provádění operací nebo implementaci přenosové funkce, která je obvykle označena velkým písmenem G. Tato funkce je matematický model, který popisuje reakci nabízené systémem na vstupní signál.

Přenosovou funkci lze vyjádřit z hlediska času t jako G (t) nebo proměnná s jako G (s).

Když vstupní signál X (y) dosáhne bloku, je vynásoben přenosovou funkcí a transformován na výstupní signál Y (y). Matematicky je to vyjádřeno takto:

Y (s) = X (s). G (s)

Ekvivalentně je přenosová funkce poměr mezi Laplaceovou transformací výstupního signálu a Laplaceovou transformací vstupního signálu za předpokladu, že počáteční podmínky systému jsou nulové:

G (s) = Y (s) / X (s)

Součet bodů

Sčítací bod nebo sčítač je symbolizován kruhem s křížem uvnitř. Používá se ke kombinování dvou nebo více signálů pomocí sčítání a odčítání. Na konec šipky, která symbolizuje znaménko, je znaménko + umístěno přímo, pokud je přidáno zmíněné znaménko, nebo znaménko -, pokud je odečteno..

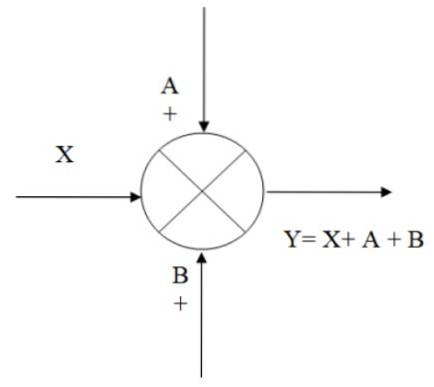
Na následujícím obrázku je příklad fungování sčítače: máme vstupní signál X, ke kterému jsou přidány signály A a B, čímž získáme výstup Y, který je algebraicky ekvivalentní:

Y = X + A + B

Bod odbočky

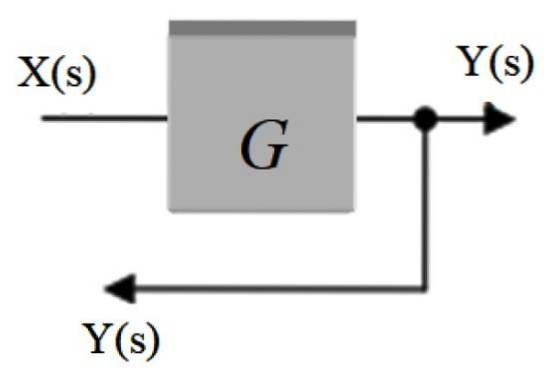
Také se tomu říká bifurkační bod. V něm je signál, který vychází z bloku, distribuován do dalších bloků nebo do sčítače. Je reprezentován bodem umístěným na signální šipce a vychází z ní další šipka, která přesměruje signál do jiné části.

Příklady pravidel blokové algebry

Jak bylo vysvětleno dříve, myšlenkou je vyjádřit systém pomocí blokového diagramu a zmenšit jej tak, aby našel přenosovou funkci, která ho popisuje. Níže jsou uvedena pravidla blokové algebry pro zjednodušení diagramů:

Kaskádové bloky

Když máte signál, který postupně prochází G bloky₁, G_dva, G₃..., je redukován na jeden blok, jehož přenosová funkce je produktem G₁, G_dva, G₃...

V následujícím příkladu vstupuje signál X do prvního bloku a jeho výstup je:

Y₁(s) = X (s) .G₁(s)

Otočte Y₁vstupuje do bloku G_dvas), jejichž výstup je:

Y_dva(s) = X (s) .G₁(s). G_dva(s)

Postup je platný pro n kaskádových bloků:

Y_n (s) = X (s). G₁(s) .G_dvas) ... G_n(s)

Paralelní bloky

V diagramu vlevo se signál X (y) rozvětvuje a vstupuje do G bloků₁s) a G._dva(s):

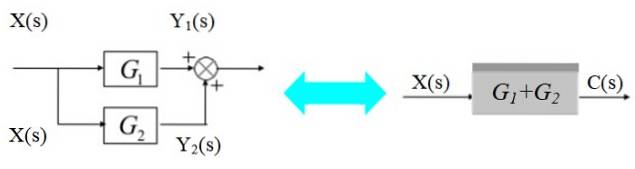
Příslušné výstupní signály jsou:

Y₁(s) = X (s) .G₁(s)

Y_dva(s) = X (s) .G_dva(s)

Tyto signály se sčítají, aby se získalo:

C (s) = Y₁(s) + Y._dva(s) = X (s). [G₁(s) + G_dva(s)]

Jak je znázorněno na obrázku vpravo.

Přesuňte zmije doleva

Sčítačku lze posunout nalevo od bloku takto:

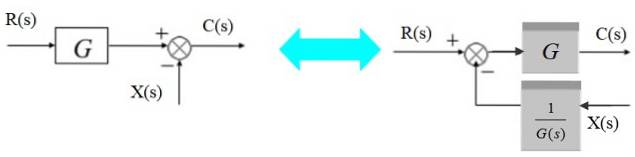
Vlevo je výstupní signál:

C (s) = R (s). G (s) - X (s)

Rovnocenně vpravo:

C (s) = [R (s) - X (s) / G (s)]. G (s)

Přesuňte zmije doprava

Sčítačku lze přesunout napravo od bloku takto:

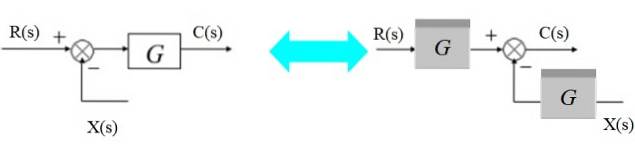
Vlevo máme: [R (s) - X (s)]. G (s) = C (s)

A vpravo:

R (s). G (s) - X (s). G (s) = C (s)

Posuňte bod větvení zleva doprava

Chcete-li přesunout bod větvení zleva doprava z bloku, pozorujte, že výstup C (s) doprava je produkt X (s) .G (s). Vzhledem k tomu, že jej chcete převést na X (s) znovu, vynásobte inverzí G (s).

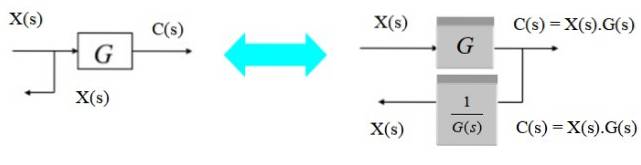
Posuňte bod větvení zprava doleva

Alternativně lze bod větvení posunout zprava doleva takto:

Protože na výstupu z větve chceme získat C (s), jednoduše vložte nový blok G (s) do bodu větve nalevo od původního bloku.

Systém zpětné vazby

V následujícím systému je výstupní signál C (y) přiváděn zpět sčítačkou vlevo:

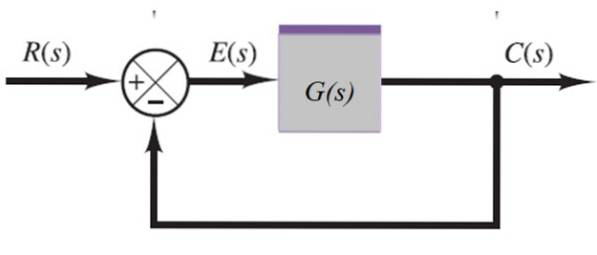
C (s) = E (s). G (s)

Ale:

E (s) = R (s) -C (s)

Nahrazením tohoto výrazu v předchozí rovnici zůstává: C (s) = [R (s) -C (s)]. G (s), ze kterých lze vyřešit C (s):

C (s) + C (s). G (s) = R (s). G (s) → C (s). [1 + G (s)] = R (s). G (s)

C (s) = R (s). G (s) / [1 + G (s)]

Nebo alternativně:

C (s) / R (s) = G (s) / [1 + G (s)]

V grafické podobě po zjednodušení zůstává:

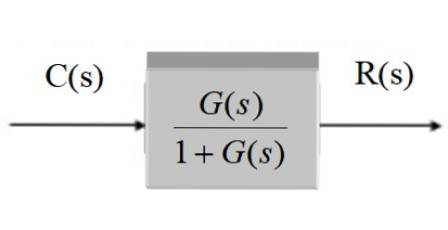
Systém se zpětnou vazbou a převodníkem

Převodník se skládá z přenosové funkce H (s):

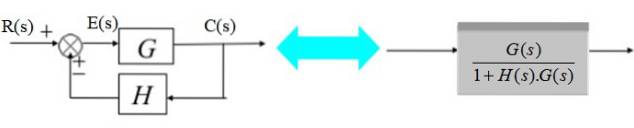
V diagramu vpravo je výstupní signál C (s):

C (s) = E (s). G (s) s E (s) = R (s) - C (s). H (s)

Pak:

C (s) = [R (s) - C (s). H (s)]. G (s)

C (s) [1+ H (s) .G (s)] = R (s) .G (s)

C (s) lze tedy vyřešit:

C (s) = G (s). R (s) / [1+ H (s) .G (s)]

A funkce přenosu bude:

G (s) / [1+ H (s). G (s)]

Jak je znázorněno na zjednodušeném diagramu vpravo.

Vyřešená cvičení

Cvičení 1

Najděte přenosovou funkci následujícího systému:

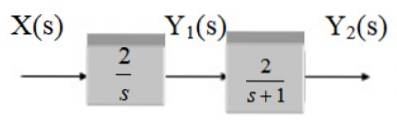
Řešení

Zachází dva bloky v kaskádě, proto je přenosová funkce součinem funkcí G₁ a G._dva.

Musí:

G₁ = 2 / s

G_dva = 2 / (s + 1)

Hledaná funkce přenosu je tedy:

G (s) = 4 / [s (s + 1)]

Cvičení 2

Snižte následující systém:

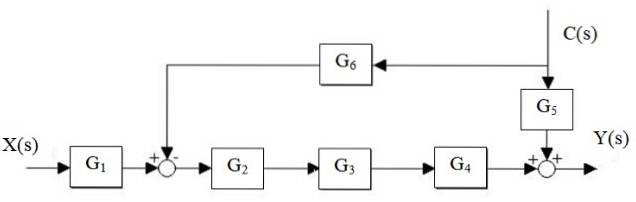
Řešení

Nejprve se sníží G kaskáda_dva, G₃ a G._4, a rovnoběžka G je oddělena₅ a G.₆:

Potom zmije nalevo od bloku G_dva ⋅G₃ ⋅ G₄ pohybuje se doprava:

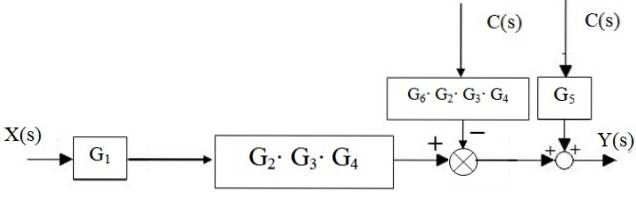
Složky na pravé straně jsou omezeny pouze na jeden, stejně jako kaskádové bloky:

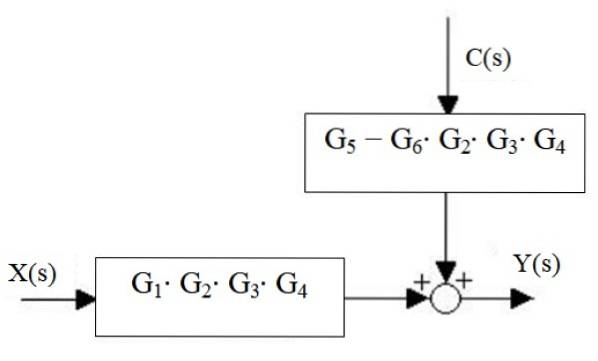
Nakonec je výstup systému:

Y (s) = X (s) ⋅G₁⋅ G_dva ⋅G₃ ⋅ G₄ + C (s) ⋅ [G₅ - G₆ ⋅ G_dva ⋅G₃ ⋅ G₄]

Reference

1. Alaydi, J. Blokové schéma řídicího systému. Obnoveno z: site.iugaza.edu.ps.
2. Bolton, W. 2006. Řídicí technika. 2. místo Edice. Alfa Omega.
3. Cwalinsky, J. Úvod do systémové blokové algebry. Obnoveno z: cedengineering.com.
4. Spojení otce. Blokový diagram. Obnoveno z: dademuch.com.
5. Ogata, K. 2010. Moderní řídicí technika. 5. Edice. Pearson.