
Vektorové základy algebry, veličiny, vektory
The vektorová algebra je obor matematiky odpovědný za studium systémů lineárních rovnic, vektorů, matic, vektorových prostorů a jejich lineárních transformací. Souvisí to s oblastmi, jako je strojírenství, řešení diferenciálních rovnic, funkční analýza, operační výzkum, počítačová grafika..
Další oblastí, kterou si lineární algebra osvojila, je fyzika, protože díky ní bylo možné vyvinout studium fyzikálních jevů a popsat je pomocí vektorů. To umožnilo lepší pochopení vesmíru.

Rejstřík článků
- 1 Základy
- 1.1 Geometricky
- 1.2 Analyticky
- 1.3 Axiomaticky
- 2 velikosti
- 2.1 Skalární velikost
- 2.2 Vektorová velikost
- 3 Co jsou vektory?
- 3.1 Modul
- 3.2 Adresa
- 3.3 Smysl
- 4 Klasifikace vektorů
- 4.1 Opravený vektor
- 4.2 Volný vektor
- 4.3 Posuvný vektor
- 5 Vlastnosti vektorů
- 5.1 vektory týmových čoček
- 5.2 Ekvivalentní vektory
- 5.3 Rovnost vektorů
- 5.4 Opačné vektory
- 5.5 Jednotkový vektor
- 5.6 Nulový vektor
- 6 Složky vektoru
- 6.1 Příklady
- 7 Operace s vektory
- 7.1 Sčítání a odčítání vektorů
- 7.2 Násobení vektorů
- 8 Reference
Základy
Vektorová algebra pocházela ze studia čtveřic (rozšíření reálných čísel) 1, i, j a k, stejně jako z karteziánské geometrie propagované Gibbsem a Heavisidem, kteří si uvědomili, že vektory budou sloužit jako nástroj pro reprezentaci různých fyzikálních jevů.
Vektorová algebra je studována na třech základních principech:
Geometricky
Vektory jsou reprezentovány čarami, které mají orientaci, a operace, jako je sčítání, odčítání a násobení reálnými čísly, jsou definovány geometrickými metodami..
Analyticky
Popis vektorů a jejich operací se provádí pomocí čísel, nazývaných komponenty. Tento typ popisu je výsledkem geometrické reprezentace, protože se používá souřadnicový systém.
Axiomaticky
Je vytvořen popis vektorů, bez ohledu na souřadnicový systém nebo jakýkoli typ geometrické reprezentace.
Studium postav ve vesmíru se provádí jejich reprezentací v referenčním systému, který může být v jedné nebo více dimenzích. Mezi hlavní systémy patří:
- Jednorozměrný systém, což je čára, kde bod (O) představuje počátek a další bod (P) určuje měřítko (délku) a jeho směr:
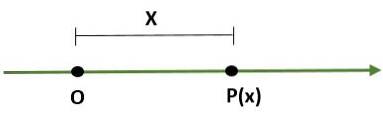
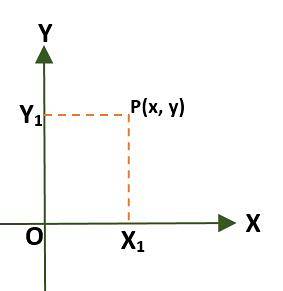
- Obdélníkový souřadnicový systém (dvourozměrný), který se skládá ze dvou kolmých čar zvaných osa x a osa y, které procházejí počátkem bodu (O); tímto způsobem je letadlo rozděleno do čtyř oblastí zvaných kvadranty. V tomto případě je bod (P) v rovině dán vzdálenostmi, které existují mezi osami a P.
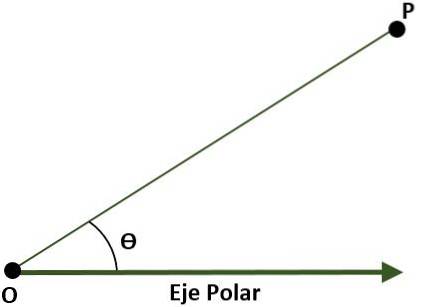
- Polární souřadnicový systém (dvourozměrný). V tomto případě se systém skládá z bodu O (počátek), který se nazývá pól, a paprsku s počátkem v O, který se nazývá polární osa. V tomto případě je bod P roviny vzhledem k pólu a polární ose dán úhlem (Ɵ), který je tvořen vzdáleností mezi počátkem a bodem P.
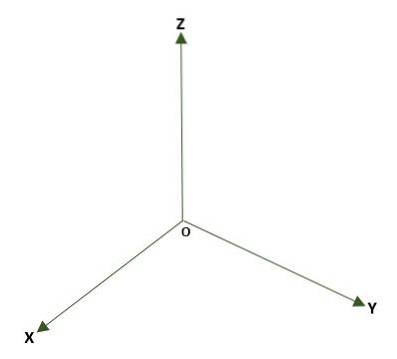
- Obdélníkový trojrozměrný systém, tvořený třemi kolmými čarami (x, y, z), jejichž počátkem je bod O v prostoru. Jsou vytvořeny tři roviny souřadnic: xy, xz a yz; prostor bude rozdělen do osmi oblastí zvaných oktanty. Odkaz na bod P v prostoru je dán vzdálenostmi, které existují mezi rovinami a P.
Veličiny
Velikost je fyzikální veličina, kterou lze spočítat nebo měřit pomocí číselné hodnoty, jako v případě některých fyzikálních jevů; často je však nutné umět popsat tyto jevy jinými než číselnými faktory. Proto jsou velikosti rozděleny do dvou typů:
Skalární velikost
Jsou to ty veličiny, které jsou definovány a reprezentovány numericky; tj. modulem spolu s měrnou jednotkou. Například:
a) Čas: 5 sekund.
b) Hmotnost: 10 kg.
c) Objem: 40 ml.
d) Teplota: 40 ° C.
Vektorová velikost
Jsou to ty veličiny, které jsou definovány a reprezentovány modulem společně s jednotkou, stejně jako smyslem a směrem. Například:
a) Rychlost: (5ȋ - 3ĵ) m / s.
b) Zrychlení: 13 m / sdva; S 45º E.
c) Síla: 280 N, 120 °.
d) Hmotnost: -40 ĵ kg-f.
Vektorové veličiny jsou graficky znázorněny vektory.
Co jsou vektory?
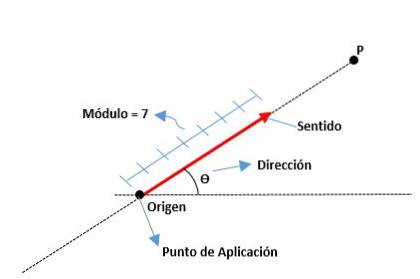
Vektory jsou grafická znázornění vektorové veličiny; to znamená, že jsou to úsečky, u nichž je jejich konečný konec špičkou šipky.
Ty jsou určeny jeho modulem nebo délkou segmentu, jeho směrem, který je označen špičkou jeho šipky, a jeho směrem podle čáry, ke které patří. Počátek vektoru je také znám jako bod aplikace.
Prvky vektoru jsou následující:
Modul
Je to vzdálenost od počátku do konce vektoru, reprezentovaná reálným číslem spolu s jednotkou. Například:
| OM | = | A | = A = 6 cm
Směr
Je to míra úhlu, která existuje mezi osou x (od kladného) a vektorem, a také se používají hlavní body (sever, jih, východ a západ).
Smysl
Je to dáno šipkou umístěnou na konci vektoru, což naznačuje, kam směřuje.
Klasifikace vektorů
Obecně jsou vektory klasifikovány jako:
Opravený vektor
Je to ten, jehož místo aplikace (původ) je pevné; to znamená, že zůstává spojeno s bodem v prostoru, takže se v něm nemůže pohybovat.
Volný vektor
Může se volně pohybovat v prostoru, protože jeho počátek se přesune do libovolného bodu, aniž by změnil svůj modul, směr nebo směr..
Jezdec vektor
Je to ten, který může přenést svůj původ podél své linie činnosti, aniž by změnil svůj modul, směr nebo směr..
Vlastnosti vektorů
Mezi hlavní vlastnosti vektorů patří:
Vektory týmové čočky
Jsou to ty volné vektory, které mají stejný modul, směr (nebo jsou rovnoběžné) a mají smysl jako posuvný vektor nebo pevný vektor.
Ekvivalentní vektory
Nastane, když dva vektory mají stejný směr (nebo jsou rovnoběžné), stejný smysl a navzdory tomu, že mají různé moduly a body aplikace, způsobují stejné efekty.
Vektorová rovnost
Ty mají stejný modul, směr a smysl, i když jsou jejich výchozí body odlišné, což umožňuje paralelnímu vektoru překládat se, aniž by to ovlivnilo..
Naproti vektory
Jsou to ti, kteří mají stejný modul a směr, ale jejich smysl je opačný.
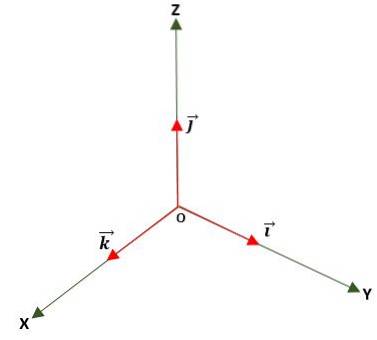
Jednotkový vektor
Je to modul, ve kterém se modul rovná jednotce (1). To se získá vydělením vektoru jeho modulem a používá se k určení směru a smyslu vektoru, a to buď v rovině, nebo v prostoru, pomocí základních nebo normalizovaných jednotkových vektorů, kterými jsou:
Nulový vektor
Je to ten, jehož modul je roven 0; to znamená, že jeho počátek a konec se shodují ve stejném bodě.
Složky vektoru
Komponenty vektoru jsou hodnoty projekcí vektoru na osy referenčního systému; V závislosti na rozkladu vektoru, který může být na dvou nebo trojrozměrných osách, budou získány dvě nebo tři složky..
Složky vektoru jsou reálná čísla, která mohou být kladná, záporná nebo dokonce nulová (0).
Pokud tedy máme vektor Ā s počátkem v pravoúhlém souřadném systému v rovině xy (dvourozměrném), projekce na ose x je Āx a projekce na ose y je Āy. Vektor bude tedy vyjádřen jako součet jeho složkových vektorů.
Příklady
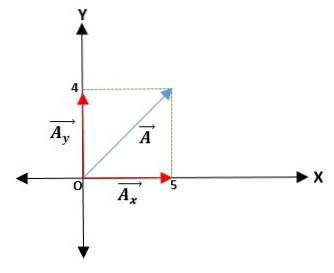
První příklad
Máme vektor Ā, který začíná od počátku a jsou uvedeny souřadnice jeho konců. Vektor Ā = (ĀX; NAY) = (4; 5) cm.
Pokud vektor Ā působí na počátku trojrozměrného trojúhelníkového souřadného systému (v prostoru) x, y, z, do jiného bodu (P), budou projekce na jeho osách Āx, Āy a Āz; vektor bude tedy vyjádřen jako součet jeho třísložkových vektorů.
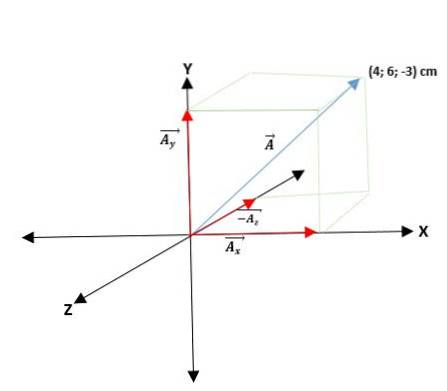
Druhý příklad
Máme vektor Ā, který začíná od počátku a jsou uvedeny souřadnice jeho konců. Vektor Ā = (AX; NAY; NAz) = (4; 6; -3) cm.
Vektory, které mají své obdélníkové souřadnice, lze vyjádřit pomocí jejich základních vektorů. K tomu musíte pouze vynásobit každou souřadnici příslušným jednotkovým vektorem takovým způsobem, že pro rovinu a prostor budou následující:
Pro rovinu: Ā = AXi + AYj.
Pro prostor: Ā = AXi + AYj + Azk.
Vektorové operace
Existuje mnoho veličin, které mají modul, smysl a směr, jako je mimo jiné zrychlení, rychlost, posunutí, síla..
Ty se používají v různých oblastech vědy a pro jejich použití je v některých případech nutné provádět operace, jako je sčítání, odčítání, násobení a dělení vektorů a skalárů..
sčítání a odčítání vektorů
Sčítání a odčítání vektorů je považováno za jedinou algebraickou operaci, protože odčítání lze zapsat jako součet; například odčítání vektorů Ā a Ē lze vyjádřit jako:
Ā - Ē = Ā + (-Ē)
Existují různé metody pro sčítání a odčítání vektorů: mohou být grafické nebo analytické.
Grafické metody
Používá se, když má vektor modul, smysl a směr. K tomu jsou nakresleny čáry, které tvoří postavu, která později pomůže určit výsledek. Mezi nejznámější patří:
Metoda rovnoběžníku
Aby bylo možné sčítat nebo odečítat dva vektory, je na ose souřadnic zvolen společný bod, který bude představovat výchozí bod vektorů, přičemž bude zachován jeho modul, směr a směr..
Čáry jsou poté nakresleny rovnoběžně s vektory, aby vytvořily rovnoběžník. Výsledný vektor je úhlopříčka, která vede od počátečního bodu obou vektorů k vrcholu rovnoběžníku:
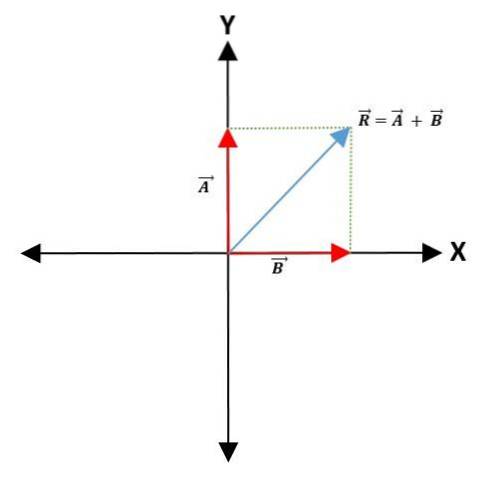
Metoda trojúhelníku
V této metodě jsou vektory umístěny jeden po druhém, přičemž si zachovávají své moduly, směry a směry. Výsledný vektor bude spojením počátku prvního vektoru s koncem druhého vektoru:
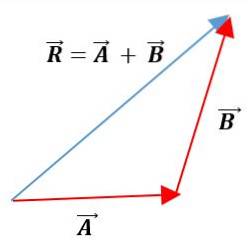
Analytické metody
Dva nebo více vektorů lze přidat nebo odečíst pomocí geometrické nebo vektorové metody:
Geometrická metoda
Když dva vektory tvoří trojúhelník nebo rovnoběžník, lze modul a směr výsledného vektoru určit pomocí zákonů sinu a kosinu. Modul výsledného vektoru je tedy pomocí kosinového zákona a metodou trojúhelníku dán vztahem:
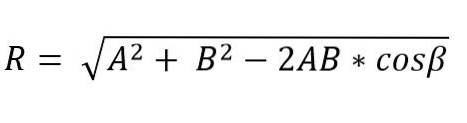
V tomto vzorci je β úhel opačný ke straně R, který se rovná 180 ° - Ɵ.
Místo toho metodou rovnoběžníku je modul výsledného vektoru:
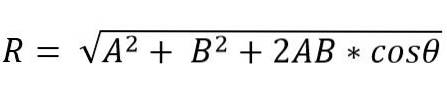
Směr výsledného vektoru je dán úhlem (α), který tvoří výslednici s jedním z vektorů.
Podle zákona sinu lze sčítání nebo odčítání vektorů provádět také metodou trojúhelníku nebo rovnoběžníku s vědomím, že v každém trojúhelníku jsou strany úměrné sinusům úhlů:
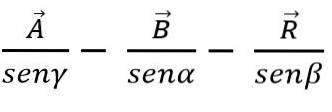
Vektorová metoda
To lze provést dvěma způsoby: v závislosti na jeho obdélníkových souřadnicích nebo základních vektorech.
Lze to provést překladem vektorů, které mají být přidány nebo odečteny směrem k počátku souřadnic, a poté všechny projekce na každou z os pro rovinu (x, y) nebo prostor (x a Z); nakonec jsou jeho komponenty přidány algebraicky. Takže pro letadlo to je:
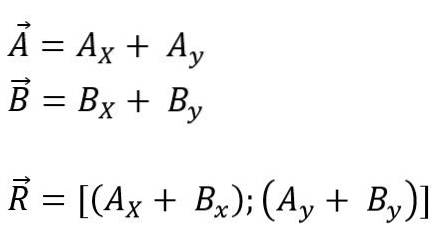
Modul výsledného vektoru je:
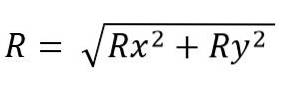
Zatímco pro prostor je to:
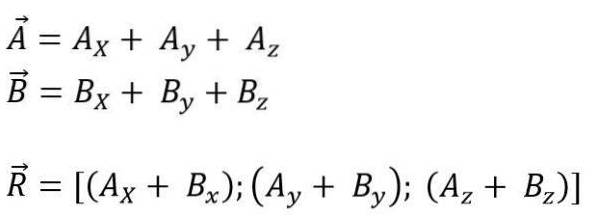
Modul výsledného vektoru je:
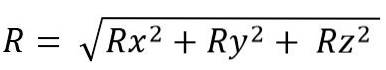
Při provádění vektorových součtů se použije několik vlastností, kterými jsou:
- Asociativní vlastnost: výslednice se nezmění, když nejprve přidáte dva vektory a poté přidáte třetí vektor.
- Komutativní vlastnost: pořadí vektorů nemění výslednici.
- Vektorová distribuční vlastnost: pokud je skalár vynásoben součtem dvou vektorů, je roven násobení skaláru každým vektorem.
- Skalární distribuční vlastnost: je-li vektor vynásoben součtem dvou skalárů, rovná se násobení vektoru pro každý skalár.
Násobení vektorů
Násobení nebo součin vektorů lze provést jako sčítání nebo odčítání, ale dělat to tímto způsobem ztrácí fyzický význam a v aplikacích se téměř nikdy nenachází. Obecně nejpoužívanějšími typy produktů jsou tedy skalární a vektorové produkty.
Skalární součin
To je také známé jako bodový produkt dvou vektorů. Když jsou moduly dvou vektorů vynásobeny kosinem nejmenšího úhlu vytvořeného mezi nimi, získá se skalární. Pro vyjádření skalárního součinu mezi dvěma vektory je mezi ně umístěn bod, který lze definovat jako:
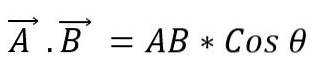
Hodnota úhlu, který existuje mezi dvěma vektory, bude záviset na tom, zda jsou rovnoběžné nebo kolmé; tedy musíte:
- Pokud jsou vektory paralelní a mají stejný smysl, kosinus 0 ° = 1.
- Pokud jsou vektory paralelní a mají opačné směry, kosinus 180 ° = -1.
- Pokud jsou vektory kolmé, kosinus 90 ° = 0.
Tento úhel lze také vypočítat s vědomím, že:

Tečkovaný produkt má následující vlastnosti:
- Komutativní vlastnost: pořadí vektorů nemění skalár.
-Distribuční vlastnost: pokud je skalár vynásoben součtem dvou vektorů, rovná se násobení skaláru každým vektorem.
Vektorový produkt
Násobení vektorů nebo součin dvou vektorů A a B povede k novému vektoru C a je vyjádřeno křížením mezi vektory:
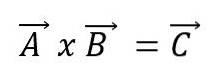
Nový vektor bude mít své vlastní charakteristiky. Tímto způsobem:
- Směr: tento nový vektor bude kolmý k rovině, která je určena původními vektory.
- Směr: toto je určeno pravidlem pravé ruky, kde se vektor A otáčí směrem k B, což ukazuje směr otáčení prsty, a směr vektoru je označen palcem.
- Modul: je určen vynásobením modulů vektorů AxB, sinusem nejmenšího úhlu, který existuje mezi těmito vektory. Vyjadřuje se:
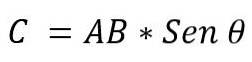
Hodnota úhlu, který existuje mezi dvěma vektory, bude záviset na tom, zda jsou rovnoběžné nebo kolmé. Je tedy možné uvést následující:
- Pokud jsou vektory paralelní a mají stejný smysl, sine 0 ° = 0.
- Pokud jsou vektory paralelní a mají opačné směry, sinus 180 ° = 0.
- Pokud jsou vektory kolmé, sinus 90 ° = 1.
Když je vektorový produkt vyjádřen jako funkce jeho základních vektorů, máme:
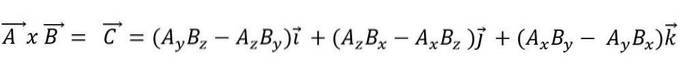
Tečkovaný produkt má následující vlastnosti:
- Není to komutativní: pořadí vektorů mění skalární.
- Distribuční vlastnost: pokud je skalár vynásoben součtem dvou vektorů, rovná se násobení skaláru každým vektorem.
Reference
- Altman Naomi, M. K. (2015). „Jednoduchá lineární regrese.“ Přírodní metody .
- Angel, A. R. (2007). Elementární algebra. Pearson Education,.
- Arthur Goodman, L. H. (1996). Algebra a trigonometrie s analytickou geometrií. Pearson Education.
- Gusiatnikov, P., & Reznichenko, S. (s.f.). Vektorová algebra v příkladech. Moskva: Mir.
- Lay, D.C. (2007). Lineární algebra a její aplikace. Pearson Education.
- Llinares, J. F. (2009). Lineární algebra: Vektorový prostor. Euklidovský vektorový prostor. University of Alicante.
- Mora, J. F. (2014). Lineární algebra. Vlast.



Zatím žádné komentáře