
Fermat omezuje to, z čeho se skládá, a vyřešená cvičení
The Fermatův limit je numerická metoda používaná k získání hodnoty sklonu úsečky, která je tečná k funkci v daném bodě v její doméně. Používá se také k získání kritických bodů funkce. Jeho výraz je definován jako:
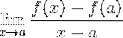
Je zřejmé, že Fermat neznal základy derivace, ale právě jeho studie podnítily skupinu matematiků k dotazování na tečny a jejich aplikace v počtu..
Rejstřík článků
- 1 Co je to Fermatův limit?
- 2 Použití Fermatova limitu pro maxima a minima
- 2.1 Kubická parabola
- 2.2 Maximum a minimum
- 2.3 Metoda
- 3 Historie
- 4 cvičení
- 4.1 Cvičení 1
- 4.2 Cvičení 2
- 5 Reference
Co je to Fermatův limit?

Skládá se z přístupu 2 bodů, které za dřívějších podmínek tvoří sečnickou čáru k funkci s průnikem v párech hodnot.
Přiblížením proměnné k hodnotě „a“ je dvojice bodů nucena se setkat. Tímto způsobem se dříve sečmá přímka stane tečnou k bodu (a; f (a)).
Hodnota kvocientu (x - a) při hodnocení v bodě „a“ poskytuje neurčitost limitů typu K mezi nulou (K / 0). Pokud je možné tyto neurčité faktory prolomit pomocí různých faktoringových technik.
Nejčastěji používané operační techniky jsou:
-Rozdíl čtverců (adva - bdva ) = (a + b) (a - b); Existence prvku (a-b) implikuje ve většině případů faktor, který zjednodušuje výraz (x-a) v kvocientu Fermatova limitu.
- Dokončení čtverců (sekeradva + bx); Po dokončení čtverců se získá Newtonův binomik, kde je jeden z jeho 2 faktorů zjednodušen výrazem (x - a), čímž dojde k prolomení neurčitosti.
- Konjugát (a + b) / (a + b); Násobení a dělení výrazu konjugátem nějakého faktoru může být velkou pomocí k prolomení neurčitosti.
- Společný faktor; V mnoha případech výsledek operace čitatele limitu Fermat f (x) - f (a) skrývá faktor (x - a) nezbytný pro faktor. Za tímto účelem je pečlivě sledováno, které prvky se opakují v každém faktoru výrazu.
Uplatnění Fermatova limitu pro maxima a minima
I když Fermatův limit nerozlišuje mezi maximem a minimem, protože dokáže identifikovat pouze kritické body podle jeho definice, běžně se používá při výpočtu omezení nebo podlaží funkcí v rovině..
Základní znalost grafické teorie funkcí ve spojení s touto větou může stačit k určení maximální a minimální hodnoty mezi funkcemi. Ve skutečnosti lze inflexní body definovat pomocí Fermatovy věty pomocí věty o střední hodnotě.
Kubická parabola
Nejvýznamnějším paradoxem pro Fermata bylo studium kubické paraboly. Protože jeho pozornost byla zaměřena na tečny čáry funkce pro daný bod, narazil na problém definování uvedené tečny v inflexním bodě funkce.
Zdálo se nemožné určit tečnou přímku k bodu. Tím začíná vyšetřování, které by vedlo k diferenciálnímu počtu. Definováno později důležitými exponenty matematiky.
Maximus a minimální
Studium maxim a minim funkce bylo výzvou pro klasickou matematiku, kde k jejich definování byla nutná jednoznačná a praktická metoda.
Fermat vytvořil metodu založenou na provozu malých diferenciálních hodnot, které jsou po faktoringových procesech eliminovány, čímž ustupuje hledané maximální a minimální hodnotě.
Tato proměnná bude muset být vyhodnocena v původním výrazu, aby se určila souřadnice uvedeného bodu, který bude společně s analytickými kritérii definován jako maximální nebo minimální výraz.
Metoda
Ve své metodě Fermat používá doslovnou symboliku Viety, která spočívá ve výlučném použití velkých písmen: samohlásky, pro neznámé a souhlásky pro známá množství.
V případě radikálních hodnot zavedl Fermat konkrétní proces, který by později byl použit při faktorizaci limitů neurčitosti nekonečno mezi nekonečny.
Tento proces spočívá v dělení každého výrazu hodnotou použitého diferenciálu. V případě Fermata použil písmeno E, kde po vydělení nejvyšší silou E se hodnota hledaná pro kritický bod stává odstranitelnou..
Příběh
Fermatův limit je ve skutečnosti jedním z nejméně renomovaných příspěvků v dlouhém seznamu matematiků. Jeho studie šla od prvočísel, aby v zásadě vytvořila základy pro výpočet.
Fermat byl zase známý svými výstřednostmi týkajícími se jeho hypotéz. Bylo běžné, že nechal nějakou výzvu ostatním matematikům té doby, když už měl řešení nebo důkaz.
Měl nejrůznější spory a spojenectví s různými matematiky té doby, kteří s ním rádi nebo nenáviděli práci.
Jeho poslední věta byla hlavní zodpovědnou za jeho světovou slávu, kde uvedl, že zobecnění Pythagorova věta pro jakýkoli stupeň „n“ to bylo nemožné. Tvrdil, že o tom má platný důkaz, ale před zveřejněním zemřel.
Tato demonstrace musela čekat přibližně 350 let. V roce 1995 matematici Andrew Wiles a Richard Taylor ukončili úzkost, kterou zanechal Fermat, a ukázali, že měl pravdu díky platnému důkazu své poslední věty.
Výcvik
Cvičení 1
Definujte sklon tečny ke křivce f (x) = xdva v bodě (4, 16)
Dosazení ve výrazu Fermatova limitu máme:
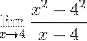
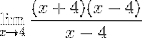
Faktory (x - 4) jsou zjednodušeny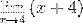
Při hodnocení máte
M = 4 + 4 = 8
Cvičení 2
Definujte kritický bod výrazu f (x) = xdva + 4x pomocí limitu Fermat
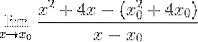
Provádí se strategické seskupování prvků, které se snaží seskupit páry X-X0
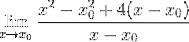
Nejmenší čtverce jsou rozvinuty
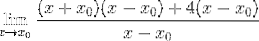
Je pozorován společný faktor X-X0 a je extrahován
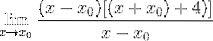
Výraz lze nyní zjednodušit a neurčitost prolomit
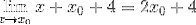
V minimálních bodech je známo, že sklon tečny je roven nule. Tímto způsobem můžeme vyrovnat nalezený výraz na nulu a vyřešit pro hodnotu X0
2 X0 + 4 = 0
X0 = -4/2 = -2
Chcete-li získat chybějící souřadnici, je nutné pouze vyhodnotit bod v původní funkci
F (-2) = (-2)dva + 4 (-2) = 4 - 8 = - 4
Kritický bod je P (-2, -4).
Reference
- Skutečná analýza. Historický přístup Sauhl Stahl, John Wiley & Sons, 5. srpna. 1999.
- Matematická kariéra Pierra de Fermata, 1601-1665: Druhé vydání. Michael Sean Mahoney. Princeton University Press, 5. června. 2018
- Od Fermata k Minkowskému: Přednášky o teorii čísel a jejím historickém vývoji. W. Scharlau, H. Opolka, Springer Science & Business Media, 1985
- Fermatova poslední věta: Genetický úvod do teorie algebraických čísel. Harold M. Edwards. Springer Science & Business Media, 14. ledna 2000
- Fermat Days 85: Mathematics for Optimization. J.-B. Hiriart-Urruty Elsevier, 1. ledna. 1986



Zatím žádné komentáře