
Měření centrální tendence pro seskupené datové vzorce, cvičení

The trendová opatření centrální označují hodnotu, kolem které jsou data distribuce. Nejznámější je průměrný nebo aritmetický průměr, který se skládá sečtením všech hodnot a vydělením výsledku celkovým počtem dat.
Pokud se však distribuce skládá z velkého počtu hodnot a nejsou prezentovány řádně, není snadné provést nezbytné výpočty k získání cenných informací, které obsahují..

Proto jsou seskupeny do tříd nebo kategorií, aby vytvořily a distribuce frekvence. Provedením tohoto předchozího uspořádání dat je pak snazší vypočítat míry centrální tendence, mezi které patří:
-Polovina
-Medián
-móda
-Geometrický průměr
-Harmonický průměr
Vzorce
Zde jsou vzorce pro míry centrální tendence pro seskupená data:
Aritmetický průměr
Průměr je nejpoužívanější pro charakterizaci kvantitativních dat (číselných hodnot), i když je docela citlivý na extrémní hodnoty distribuce. Vypočítává se podle:

S:
-X: průměrný nebo aritmetický průměr
-Fi: frekvence třídy
-mi: známka třídy
-g: počet tříd
-n: celková data
Medián
Pro jeho výpočet je nutné najít interval, který obsahuje pozorování n / 2, a interpolovat k určení numerické hodnoty uvedeného pozorování pomocí následujícího vzorce:

Kde:
-c: šířka intervalu, ke kterému medián patří
-BM: dolní mez uvedeného intervalu
-Fm: počet pozorování obsažených v intervalu
-n / 2: celková data dělená 2.
-FBM: počet pozorování před intervalu obsahujícího medián.
Medián je tedy míra polohy, to znamená, že rozděluje soubor dat na dvě části. Mohou být také definovány kvartily, decilů Y percentily, které rozdělují distribuci na čtyři, deset a sto částí.
móda
Ve sdružených datech se prohledává třída nebo kategorie, která obsahuje nejvíce pozorování. To je modální třída. Distribuce může mít dva nebo více režimů, v takovém případě se nazývá bimodální Y multimodální, resp.
Režim můžete také vypočítat ve seskupených datech podle rovnice:

S:
-L1: spodní limit třídy, kde je režim nalezen
-Δ1: odečíst mezi frekvencí modální třídy a frekvencí třídy, která jí předchází.
-Δdva: odečíst mezi frekvencí modální třídy a frekvencí následující třídy.
-c: šířka intervalu obsahujícího režim
Harmonický průměr
Harmonický průměr je označen H. Když máte množinu n hodnoty x1, Xdva, X3..., Harmonický průměr je inverzní nebo převrácený k aritmetickému průměru inverzních hodnot.
Je to jednodušší vidět pomocí vzorce:

A když jsou k dispozici seskupená data, výraz se stává:

Kde:
-H: harmonický průměr
-Fi: frekvence třídy
-mi: značka třídy
-g: počet tříd
-N = f1 + Fdva + F3 +...
Geometrický průměr
Pokud ano n kladná čísla x1, Xdva, X3…, Jeho geometrický průměr G se vypočítá n-tou odmocninou součinu všech čísel:

V případě seskupených dat lze ukázat, že dekadický logaritmus geometrického průměru log G je dán vztahem:

Kde:
-G: geometrický průměr
-Fi: frekvence třídy
-mi: známka třídy
-g: počet tříd
-N = f1 + Fdva + F3 +...
Vztah mezi H, G a X
Vždy platí, že:
H ≤ G ≤ X
Nejpoužívanější definice
K vyhledání hodnot popsaných ve vzorcích výše jsou vyžadovány následující definice:
Frekvence
Frekvence je definována jako počet opakování části dat.
Hodnost
Je to rozdíl mezi nejvyšší a nejnižší hodnotou přítomnou v distribuci.
Počet tříd
Abychom věděli, do kolika tříd seskupujeme data, použijeme některá kritéria, například následující:

Limity
Jsou volány extrémní hodnoty každé třídy nebo intervalu limity a každá třída může mít jak dobře definované limity, v takovém případě má nižší a vyšší limit. Nebo může mít otevřené limity, když je uveden rozsah, například hodnot větších nebo menších než určitý počet.
Značka třídy
Jednoduše se skládá ze středu intervalu a vypočítá se zprůměrováním horní a dolní meze.
Šířka mezery
Data lze seskupit do tříd stejné nebo různé velikosti, to je šířka nebo šířka. První možnost je nejpoužívanější, protože výrazně usnadňuje výpočty, i když v některých případech je nutné, aby třídy měly různé šířky.
Šířka C Interval lze určit podle následujícího vzorce:
c = Rozsah / NC
KdeC je počet tříd.
Cvičení vyřešeno
Níže máme sérii měření rychlosti v km / h, pořízených radarem, což odpovídá 50 autům, která prošla ulicí v určitém městě:
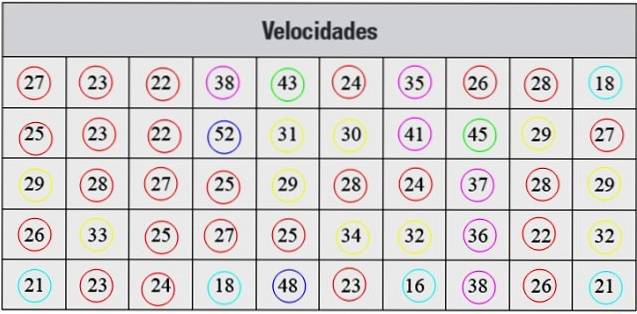
Řešení
Takto prezentovaná data nejsou organizována, takže prvním krokem je jejich seskupení do tříd.
Kroky ke seskupení dat a sestavení tabulky
Krok 1
Najděte rozsah R:
R = (52-16) km / h = 36 km / h
Krok 2
Vyberte počet tříd NC, podle daných kritérií. Jelikož existuje 50 dat, můžeme zvolit NC = 6.
Krok 3
Vypočítejte šířku C intervalu:
c = Rozsah / NC = 36/6 = 6
Krok 4
Třídy formulářů a skupinová data následovně: pro první třídu je jako dolní mez zvolena hodnota o něco menší než nejnižší hodnota uvedená v tabulce, k této hodnotě je přidána hodnota c = 6, která byla dříve vypočítána, tedy získá horní hranici první třídy.
Stejným způsobem postupujeme při sestavování zbytku tříd, jak ukazuje následující tabulka:
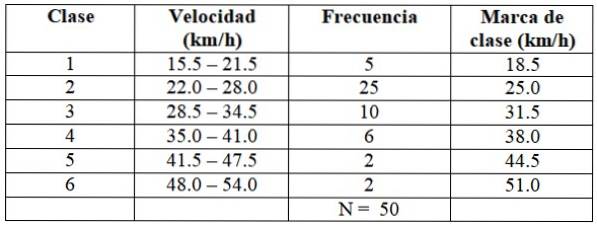
Každá frekvence odpovídá barvě na obrázku 2, čímž je zajištěno, že z počítání neunikne žádná hodnota..
Výpočet střední hodnoty

X = (5 x 18,5 +25 x 25,0 + 10 x 31,5 + 6 x 38,0 + 2 x 44,5 + 2 x 51,0) ÷ 50 = 29,03 km / h
Výpočet mediánu

Medián je ve třídě 2 tabulky, protože existuje prvních 30 dat distribuce.
-Šířka intervalu, ke kterému medián patří: c = 6
-Dolní hranice intervalu, kde je medián: BM = 22,0 km / h
-Počet pozorování, která obsahuje interval fm = 25
-Celková data dělená 2: 50/2 = 25
-Počet pozorování je před intervalu obsahujícího medián: fBM = 5
A operace je:
Medián = 22,0 + [(25-5) ÷ 25] × 6 = 26,80 km / h
Výpočet módy

Móda je také ve třídě 2:
-Šířka intervalu: c = 6
-Dolní mez třídy, kde se režim nachází: L1 = 22,0
-Odečtěte mezi frekvencí modální třídy a frekvencí třídy, která jí předchází: Δ1 = 25-5 = 20
-Odečtěte mezi frekvencí modální třídy a frekvencí následující třídy: Δdva = 25 - 10 = 15
S těmito daty je operace:
Režim = 22,0 + [20 ÷ (20 + 15)] x6 = 25,4 km / h
Výpočet geometrického průměru
N = f1 + Fdva + F3 +… = 50
log G = (5 x log 18,5 + 25 x log 25 + 10 x log 31,5 + 6 x log 38 + 2 × log 44,5 + 2 x log 51) / 50 =
log G = 1,44916053
G = 28,13 km / h
Výpočet harmonického průměru

1 / V = (1/50) x [(5 / 18,5) + (25/25) + (10 / 31,5) + (6/38) + (2 / 44,5) + (2/51)] = 0,0366
H = 27,32 km / h
Souhrn opatření centrální tendence
Jednotky proměnných jsou km / h:
-Průměr: 29.03
-Medián: 26,80
-Móda: 25.40
-Geometrický průměr: 28,13
-Harmonický průměr: 27,32
Reference
- Berenson, M. 1985. Statistiky pro management a ekonomiku. Interamericana S.A.
- Canavos, G. 1988. Pravděpodobnost a statistika: Aplikace a metody. Mcgraw kopec.
- Devore, J. 2012. Pravděpodobnost a statistika pro inženýrství a vědu. 8. Edice. Cengage.
- Levin, R. 1988. Statistiky pro správce. 2. místo Edice. Hala Prentice.
- Spiegel, M. 2009. Statistiky. Série Schaum. 4. místo Edice. Mcgraw kopec.
- Zpracování seskupených údajů. Obnoveno z: itchihuahua.edu.mx.
- Walpole, R. 2007. Pravděpodobnost a statistika pro strojírenství a vědy. Pearson.


Zatím žádné komentáře