The rotační pohyb Země je ten, kolem kterého naše planeta pobíhá Osa Země ve směru západ-východ a trvá přibližně jeden den, konkrétně 23 hodin, 56 minut a 3,5 sekundy.
Tento pohyb, spolu s translací kolem Slunce, jsou tím nejdůležitějším, co Země má. Zejména rotační pohyb má v každodenním životě živých bytostí velký vliv, protože vede ke vzniku dnů a nocí.
Proto má každý časový interval určité množství slunečního osvětlení, kterému se běžně říká den, a absence slunečního světla nebo noc. Rotace Země také přináší změny teploty, protože den je obdobím oteplování, zatímco noc je obdobím ochlazování..
Tyto okolnosti znamenají milník ve všech živých bytostech, které obývají planetu, což vede k mnoha adaptacím, pokud jde o životní návyky. Podle něj společnosti stanovily období činnosti a odpočinku podle svých zvyků a ovlivněných prostředím..
Je zřejmé, že se světlá a tmavá zóna mění, jak probíhá pohyb. Když rozdělíme 360 °, který má obvod, mezi 24 hodinami, na které se den zaokrouhlí, se ukáže, že za 1 hodinu se Země otočila o 15 ° ve směru západ-východ.
Pokud se tedy přesuneme na západ o 15 °, je to o hodinu dříve, k opačnému dojde, pokud cestujeme na východ.
Rychlost rotace Země na její vlastní ose byla odhadnuta na 1600 km / h na rovníku, s následným poklesem, jak se přibližuje k pólům, dokud se nezruší jen na ose rotace..
Rejstřík článků
Důvod, proč se Země otáčí kolem své osy, spočívá v počátcích sluneční soustavy. Možná, že Slunce strávilo dlouhou dobu teprve poté, co gravitace umožnila jeho zrození z amorfní hmoty, která obývá vesmír. Když se Slunce formovalo, získalo rotaci poskytovanou primitivním mrakem hmoty..
Část hmoty, která dala vzniknout hvězdě, byla zhutněna kolem Slunce a vytvořila planety, které také měly svůj podíl na momentu hybnosti původního mraku. Tímto způsobem mají všechny planety (včetně Země) svůj vlastní rotační pohyb ve směru západ-východ, kromě Venuše a Uranu, které se otáčejí opačným směrem..
Někteří věří, že Uran se srazil s jinou planetou podobné hustoty a v důsledku nárazu změnil jeho osu a směr otáčení. Na Venuši by existence plynných přílivů mohla vysvětlit, proč se směr otáčení v průběhu času pomalu obracel.
Moment hybnosti je v rotaci to, co je lineární hybnost k překladu. Pro těleso rotující kolem pevné osy, jako je Země, je jeho velikost dána vztahem:
L = Iω
V této rovnici L je moment hybnosti (kg.mdva/ s), Já je moment setrvačnosti (kg.mdva) Y w je úhlová rychlost (radiány / s).
Moment hybnosti je zachován, pokud na systém nepůsobí žádný čistý točivý moment. V případě vzniku sluneční soustavy je Slunce a hmota, která vedla k vzniku planet, považováno za izolovanou soustavu, na kterou žádná síla nezpůsobovala vnější točivý moment.
Za předpokladu, že Země je dokonalá koule a chová se jako tuhé těleso a na základě dodaných dat je třeba najít její moment hybnosti rotace: a) kolem své vlastní osy ab) v jejím translačním pohybu kolem Slunce.
Data: moment setrvačnosti koule = Ikoule = (2/5) MRdva; pevnina M = 5,9721024 Kg, poloměr Země R = 6371 Km; střední vzdálenost mezi Zemí a Sluncem Rm = 149,6 x 106 Km.
a) Nejprve je nutné mít moment setrvačnosti Země považován za kouli o poloměru R a hmotnosti M.
I = (2/5) '' 5 972 1024 Kg '(6371'103 Km)dva = 9,7 '1037 kg.mdva
Úhlová rychlost se vypočítá takto:
ω = 2π/ T
Kde T je doba pohybu, která je v tomto případě 24 hodin = 86400 s, proto:
ω = 2π/ T = 2π/ 86400 s = 0,00007272 s-1
Moment hybnosti rotace kolem vlastní osy je:
L = 9,7 '1037 kg.mdva'' 0,00007272 s-1 = 7,05'1033 kg.mdva/ s
b) Pokud jde o translační pohyb kolem Slunce, lze Zemi považovat za bodový objekt, jehož moment setrvačnosti je I = M.R.dvam
I = M.R.dvam= 5 972 1024 Kg''(149,6 '' 106 × 1000 m)dva = 1. 33'1047kg.mdva
Za rok je 365 ×24 × 86400 s = 3,1536 × 107 s, orbitální úhlová rychlost Země je:
ω = 2π/ T = 2π/3,1536 × 107 s = 1,99 ×10-7 s-1
S těmito hodnotami je orbitální moment hybnosti Země:
L = 1,33'1047kg.mdva × 1 .99 × 10-7 s-1 = 2,65 × 1040 kg.mdva/ s
Jak bylo uvedeno výše, posloupnost dnů a nocí, s jejich příslušnými změnami v hodinách světla a teploty, jsou nejdůležitějším důsledkem rotačního pohybu Země po vlastní ose. Jeho vliv však trochu přesahuje tuto rozhodující skutečnost:
- Rotace Země úzce souvisí s tvarem planety. Země není dokonalá koule jako kulečníková koule. Při otáčení se vyvíjejí síly, které jej deformují, což způsobuje vyboulení na rovníku a následné zploštění na pólech..
- Deformace Země vede k malým výkyvům hodnoty gravitačního zrychlení G na různých místech. Například hodnota G je větší na pólech než na rovníku.
- Rotační pohyb významně ovlivňuje distribuci oceánských proudů a výrazně ovlivňuje větry, vzhledem k tomu, že masy vzduchu a vody zažívají odchylky od své dráhy ve směru hodinových ručiček (severní polokoule) i ve směru hodinových ručiček..
- The časová pásma, aby bylo možné regulovat plynutí času na každém místě, protože různé oblasti Země jsou osvětlovány sluncem nebo potemňovány.
Coriolisův efekt je důsledkem rotace Země. Vzhledem k tomu, že ve všech rotacích dochází ke zrychlení, není Země považována za setrvačný referenční rámec, což je to, co je potřeba k uplatnění Newtonových zákonů.
V tomto případě se objeví takzvané pseudosíly, síly, jejichž původ není fyzický, jako je odstředivá síla, kterou cestující v automobilu zažívají, když tvoří křivku, a mají pocit, že jsou vychýleni na jednu stranu..
Chcete-li si představit jeho účinky, zvažte následující příklad: na platformě jsou dva lidé A a B v rotaci proti směru hodinových ručiček, oba v klidu s ohledem na ni. Osoba A hodí míč osobě B, ale když míč dosáhne místa, kde byl B, už se pohnul a míč je vychýlen na vzdálenost. s, procházející za B.
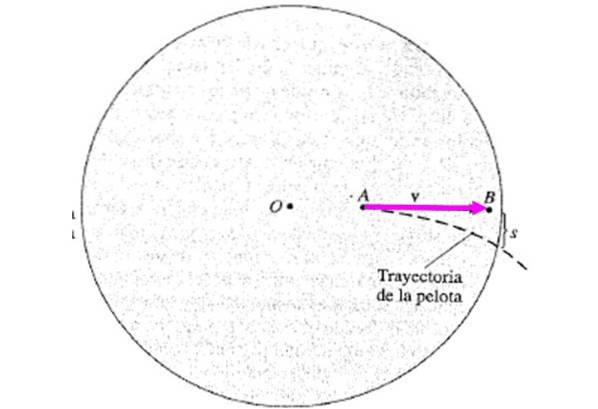
Odstředivá síla v tomto případě není odpovědná, působí již mimo střed. Toto je Coriolisova síla, jejímž účinkem je boční odklonění míče. Stává se, že A i B mají různé rychlosti vzhůru, protože jsou v různých vzdálenostech od osy otáčení. Rychlost B je vyšší a jsou dány vztahem:
protiNA = ωRNA ; protiB = ωRB
Coriolisovo zrychlení má významné účinky na pohyb vzdušných hmot, a proto ovlivňuje klima. Proto je důležité vzít v úvahu studium, jak se pohybují vzdušné proudy a oceánské proudy..
Lidé to také mohou zažít, když se pokoušejí chodit na rotující plošině, jako je pohyblivý kolotoč..
U případu zobrazeného na předchozím obrázku předpokládejme, že gravitace není brána v úvahu a pohyb je vizualizován z inerciálního referenčního systému, vně platformy. V tomto případě tah vypadá takto:
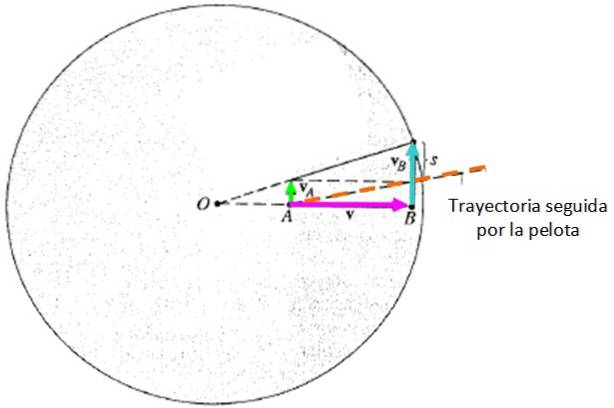
Odchylka s, kterou míč zažil z původní polohy osoby B, je:
s = sB - sNA = vt = (vB - protiNA) t = (ωRB - ωRNA) t = = ω(R.B - RNA) t
Ale RB - RNA = vt, pak:
s = ω .(vt). t = ωvtdva
Jedná se o pohyb s počáteční rychlostí 0 a konstantním zrychlením:
s = ½ aCoriolis tdva
naCoriolis = 2ω.proti
Zatím žádné komentáře