
Pohyb kyvadla
Co je to pohyb kyvadla?
The pohyb kyvadla Jedná se o pohyb tam a zpět prováděný více či méně těžkým předmětem zvaným kyvadlo, zavěšený na laně nebo lehké tyči, upevněný na druhém konci.
Kyvadlo dostane počáteční impuls a nechá se oscilovat, čímž objekt popisuje oblouky tam a zpět. To je princip, jak kyvadlové hodiny, houpačky, houpací křesla a metronomy kyvadlo, které se používá k označení časů v hudbě.
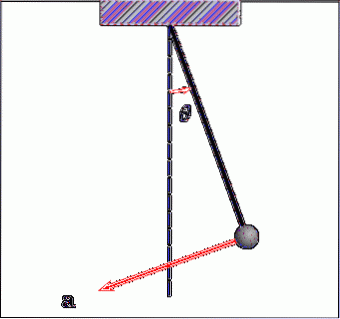
Říká se, že kolem roku 1581 pozoroval Galileo Galilei oscilaci lampy v katedrále v Pise, přičemž si všiml, že ačkoli amplituda oscilace svícen se snižovala v důsledku tření se vzduchem, nikoliv po dobu trvání cyklu lampy..
To upoutalo pozornost Galilea, který se rozhodl ve studiu pokračovat a zjistil, že doba kyvadla nezávisí na hmotnosti, ale na druhé odmocnině délky akordu, jak bude vidět později..
Charakteristika pohybu kyvadla
Kyvadlo se staví velmi snadno, protože stačí olovnice visící z bavlněné nitě a na druhém konci držená prsty nebo jej připevnit k podpěře jako hřebík..
Po malém počátečním impulsu má váha na starosti udržování oscilace kyvadla, i když tření snižuje amplitudu pohybu, až nakonec úplně ustane..
Hlavní charakteristikou kyvadlového pohybu je opakování, protože se jedná o pohyb tam a zpět. Nyní je pro usnadnění studia vhodné provést některá zjednodušení zaměřená na jednodušší model zvaný jednoduché kyvadlo.
Jednoduché kyvadlo

Je to ideální systém, který se skládá z olovnice považované za bodovou hmotu m, připevněn k lehkému, neroztažitelnému lanu délky L. Vlastnosti tohoto systému jsou:
- Mějte opakující se a periodický pohyb, který spočívá v pohybu sem a tam po obvodu oblouku o poloměru rovném L.
- Nezohledňuje tření.
- Rozsah pohybu je malý (< 5º).
- Období je nezávislé na hmotnosti m, a záleží pouze na délce L kyvadlo.
Vzorce a rovnice
Následuje diagram jednoduchého kyvadla, na které působí dvě síly: váha P o velikosti mg, která je směrována svisle dolů a napětí T Na laně. Tření se neuvažuje.
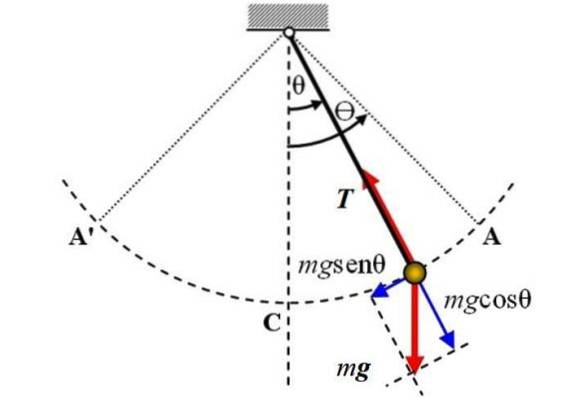
Referenční osa je svislá osa a shoduje se s polohou θ = 0, odtud se měří úhlové posunutí θ, a to buď v jednom nebo v jiném směru. Znaménko + lze přiřadit pravému posunu na obrázku.
Ke studiu pohybu kyvadla je vybrán souřadný systém s počátkem samotného kyvadla. Tento systém má tangenciální souřadnici k oblouku obvodu A'CA popsanou kyvadlem a také radiální souřadnici směřující do středu trajektorie..
V okamžiku znázorněném na obrázku se kyvadlo pohybuje doprava, ale tangenciální složka gravitace, zvaná Ft, je zodpovědný za jeho návrat. Z obrázku je patrné, že tato součást má opačný směr pohybu.
Pokud jde o napětí v laně, je vyváženo složkou hmotnosti mgcosθ.

Úhlový posun
Rovnici musíme vyjádřit pomocí jediné proměnné, pamatujeme-li, že úhlové posunutí θ a obloukový oblouk souvisejí s rovnicí:
s = L.θ
Hmota se ruší na obou stranách a pokud je amplituda malá, také úhel θ, takže platí následující aproximace:
sen θ ≈ θ
Tím se získá následující diferenciální rovnice pro proměnnou θ (t):


Tuto rovnici lze snadno vyřešit, protože jejím řešením je funkce, jejíž druhou derivací je funkce sama. Existují tři alternativy: kosinus, sinus nebo exponenciál. Kosinová funkce je vybrána pro úhlové posunutí θ (t), protože se jedná o dobře známou a snadno ovladatelnou funkci.
Čtenář může ověřit dvojím rozlišením, že následující funkce splňuje diferenciální rovnici:
θ (t) = θm cos (ωt + φ)
Kde θm je maximální úhel, kterým se kyvadlo pohybuje vzhledem k vertikále, a úhlová frekvence ω je:

Rovnice období
Období T pohybu je doba potřebná k provedení cyklu a je definována jako:

Nahrazení ω:

Jak bylo uvedeno výše, perioda nezávisí na hmotnosti kyvadla, ale pouze na jeho délce..
Příklady kyvadlového pohybu
Měření srdeční frekvence
Galileo měl nápad měřit srdeční frekvenci lidí a upravit délku kyvadla tak, aby se období shodovalo s údery srdce člověka.
Kyvadlové hodiny
Toto je nepochybně jeden z nejznámějších příkladů pohybu kyvadla. Výroba kyvadlových hodin je jak o vědě, tak o umění. Nizozemský fyzik Christian Huygens (1629-1695) vyvinul první kyvadlové hodiny v roce 1656 na základě studie provedené před lety Galileem.
Foucaultovo kyvadlo

Je to poněkud odlišné kyvadlo, než které bylo popsáno výše, protože je schopné otáčet se v jakékoli svislé rovině. Byl vytvořen francouzským fyzikem Léonem Foucaultem (1819-1868) a slouží k vizualizaci rotace Země.
Cvičení vyřešeno
Jednoduché kyvadlo prochází rovnovážnou polohou každých 0,5 s. Jaká je délka vlákna?
Řešení
Protože období je čas potřebný k dokončení úplného cyklu, ve kterém prochází rovnovážnou polohou dvakrát: jeden probíhá a druhý zpět, pak:
T = 2 × 0,5 s = 1 s
Z:

Délka L závitu je vymazána:

Nit má délku 0,25 m nebo 25 cm.
Reference
- Figueroa, D. (2005). Série: Fyzika pro vědu a techniku. Svazek 2. Dynamika. Upravil Douglas Figueroa (USB).
- Giambattista, A. 2010. Fyzika. 2. místo Ed. McGraw Hill.
- Giancoli, D. 2006. Fyzika: Principy s aplikacemi. 6.. Hala Ed Prentice.
- Katz, D. 2013. Fyzika pro vědce a inženýry. Základy a spojení. Cengage Learning.
- Knight, R. 2017. Fyzika pro vědce a inženýrství: strategický přístup. Pearson.


Zatím žádné komentáře