The rovnoměrně zrychlený přímočarý pohyb Je to ten, který běží po přímce a ve kterém mobil zvyšuje nebo snižuje svou rychlost konstantní rychlostí. Tato rychlost je velikost, která popisuje rychlost, s jakou se rychlost mění a je volána akcelerace.
V případě rovnoměrně zrychleného nebo proměnlivého přímočarého pohybu (MRUV) je za změnu velikosti rychlosti odpovědné konstantní zrychlení. U jiných typů pohybu je zrychlení také schopné změnit směr a smysl pro rychlost, nebo dokonce jen změnit směr, jako u rovnoměrného kruhového pohybu..
Protože zrychlení představuje změnu rychlosti v čase, jsou jeho jednotky v mezinárodním systému m / sdva (metrů za sekundu na druhou). Stejně jako rychlosti lze zrychlení přiřadit kladné nebo záporné znaménko v závislosti na tom, zda se rychlost zvyšuje nebo snižuje..
Zrychlení řekněme +3 m / sdva znamená, že každou sekundu se rychlost mobilního telefonu zvýší o 3 m / s. Pokud na začátku pohybu (při t = 0) byla rychlost mobilního telefonu +1 m / s, pak po jedné sekundě bude 4 m / s a po 2 sekundách bude 7 m / s.
Při rovnoměrně proměnlivém přímočarém pohybu se berou v úvahu změny rychlosti, které pohybující se objekty denně zažívají. Toto je realističtější model než rovnoměrný přímočarý pohyb. Přesto je stále poměrně omezený, protože omezuje pohyb mobilního telefonu pouze po přímce.
Rejstřík článků
Toto jsou hlavní charakteristiky rovnoměrně zrychleného přímočarého pohybu:
-Pohyb vždy probíhá po přímce.
-Zrychlení mobilního telefonu je konstantní, a to jak ve velikosti, tak ve směru a smyslu.
-Rychlost mobilních zařízení se zvyšuje (nebo snižuje) lineárně.
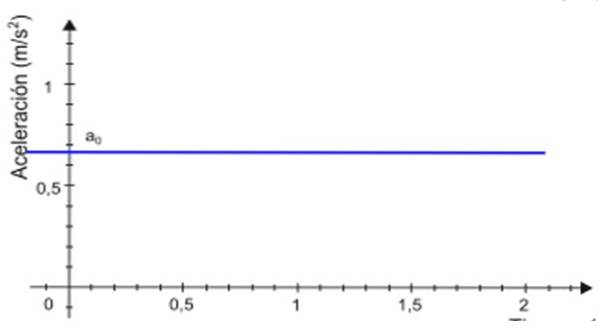
-Od zrychlení na zůstává konstantní v průběhu času t, graf jeho velikosti jako funkce času je přímka. V příkladu znázorněném na obrázku 2 je čára zbarvena modře a hodnota zrychlení se čte na svislé ose, přibližně +0,68 m / sdva.
-Graf rychlosti proti o t je to přímka (na obrázku 3 zeleně), jejíž sklon se rovná zrychlení mobilního telefonu. V příkladu je sklon kladný.
-Řez se svislou osou označuje počáteční rychlost, v tomto případě je to 0,4 m / s.
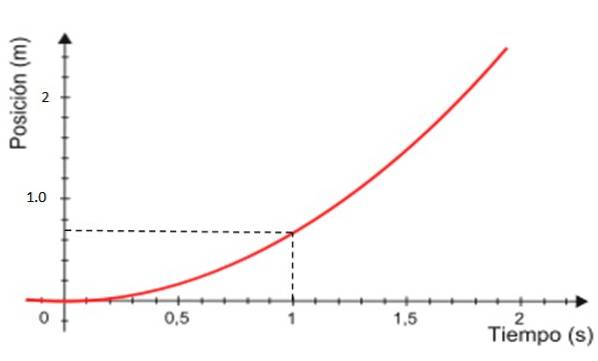
-Nakonec je grafem polohy x versus čas křivka zobrazená červeně na obrázku 4, což je vždy parabola.
Tím, že máme graf v vs. t, výpočet vzdálenosti ujeté mobilním telefonem je velmi snadný. Ujetá vzdálenost se rovná ploše pod čarou, která se nachází v požadovaném časovém intervalu.
V uvedeném příkladu předpokládejme, že chcete znát vzdálenost, kterou mobilní telefon ujel mezi 0 a 1 sekundou. Pomocí tohoto grafu viz obrázek 5.
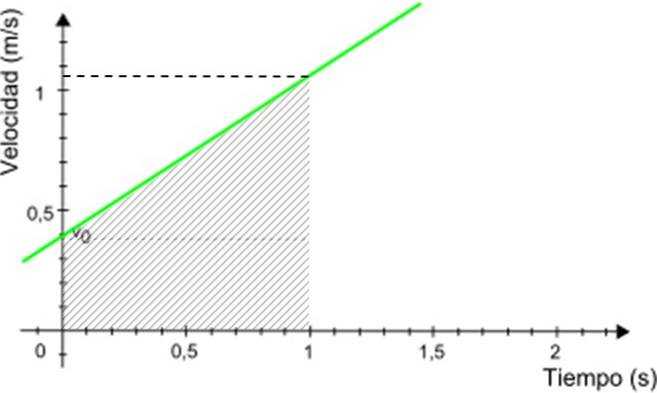
Hledaná vzdálenost je číselně ekvivalentní ploše lichoběžníku stínované na obrázku 3. Plocha lichoběžníku je dána vztahem: (hlavní základna + vedlejší základna) x výška / 2
Ujetá vzdálenost = (0,4 + 1,05) x 1/2 m = 0,725 m
Je také možné rozdělit stínovanou oblast na trojúhelník a obdélník, vypočítat odpovídající oblasti a sečíst je dohromady. Ujetá vzdálenost je kladná, i když částice jde doprava nebo doleva.
Průměrné zrychlení i okamžité zrychlení mají v MRUV stejnou hodnotu, proto:
-Akcelerace: na = konstantní
Když je zrychlení rovné 0, je pohyb rovnoměrný přímočarý, protože rychlost by v tomto případě byla konstantní. Znamení na Může to být pozitivní nebo negativní.
Protože zrychlení je sklon přímky v proti t, rovnice v (t) je:
-Rychlost jako funkce času: v (t) = vnebo + na
Kde protinebo je hodnota počáteční rychlosti mobilního telefonu
-Pozice jako funkce času: x (t) = xnebo + protinebo t + ½atdva
Když nemáte čas, ale místo toho máte rychlosti a posunutí, existuje velmi užitečná rovnice, která se získá řešením času v (t) = vnebo + na a dosadíme to do poslední rovnice. Jde o:
-Rovnice, která neobsahuje čas: protidva = vnebodva +2.a.ΔX
Při řešení kinematického cvičení je důležité zajistit, aby se situace přizpůsobila použitému modelu. Například rovnice rovnoměrného přímočarého pohybu neplatí pro zrychlený pohyb.
A ty se zrychleným pohybem neplatí například pro kruhový nebo křivočarý pohyb. První z těchto cvičení řešených níže kombinuje dva mobily s různými pohyby. K jeho správnému vyřešení je nutné přejít na příslušný model pohybu.
Chcete-li zjistit hloubku studny, dítě upustí minci a současně aktivuje svůj časovač, který se zastaví ihned poté, co uslyšíte, že mince narazí na vodu. Jeho čtení bylo 2,5 sekundy. S vědomím, že rychlost zvuku ve vzduchu je 340 m / s, vypočítejte hloubku studny.
Být h hloubka studny. Mince cestuje po této vzdálenosti volným pádem, rovnoměrně proměnlivým vertikálním pohybem, s počáteční rychlostí 0, jak je mince padána, a stálým zrychlením směrem dolů rovným 9,8 m / sdva. Udělejte si čas tm při tom.
Jakmile mince zasáhne vodu, zvuk způsobený kliknutím přejde nahoru k uchu dítěte, které zastaví stopky, jakmile to uslyší. Není důvod se domnívat, že se rychlost zvuku mění, jak stoupá studna, takže pohyb zvuku je rovnoměrný přímočarý. Zvuk chvíli trvá ts dostat se k dítěti.
h = ½.g.t.m dva = 4,9 tm dva
Kde byly nahrazeny X Y na rovnice pro polohu uvedenou v předchozí části, o h Y G.
h = vs . ts = 340 ts
Je to o známé rovnici vzdálenost = rychlost x čas. S těmito dvěma rovnicemi máme tři neznámé: h, tm a ts. V době, kdy existuje vztah, je známo, že všechno trvá 2,5 sekundy, a proto:
tm + ts = 2,5 s
Rovnice obou rovnic:
4,9 tm dva = 340 ts
Vymazání jednou a nahrazení:
4,9 tm dva= 340. (2,5 - tm)
Rozvinutím termínu vpravo a transpozicí termínů získáme:
4,9 tm dva+340 tm - 850 = 0
Toto je kvadratická rovnice se dvěma řešeními: 2.416 a -71.8. Je zvoleno pozitivní řešení, které dává smysl, protože čas nemůže být záporný a v každém případě musí být kratší než 2,5 sekundy. Pro tuto dobu se získá nahrazením hloubky studny:
4,9 tm dva= 4,9 x 2,416dva m = 28,6 m
Auto jedoucí rychlostí 90 km / h se blíží křižovatce se semaforem. Když je to 70 m odtud, rozsvítí se žluté světlo, které trvá 4 sekundy. Vzdálenost mezi semaforem a další zatáčkou je 50 m.
Řidič má tyto dvě možnosti: a) brzdit rychlostí - 4 m / sdva nebo b) zrychlit na + 2 m / sdva. Která ze dvou možností umožňuje řidiči zastavit nebo projet celou cestu, než se světlo zčervená?
Výchozí poloha řidiče je x = 0, když vidí rozsvícení žlutého světla. Je důležité správně převést jednotky: 90 km / h se rovná 25 m / s.
Podle možnosti a) řidič za 4 sekundy, které vydrží žluté světlo, jede:
x (t) = vnebo t + ½atdva= 25,4 - 1/2. (- 4) .4dvam = 68 m (Zastaví se 2 metry před semaforem)
Analýza možnosti b) máme:
x (t) = vnebo t + ½atdva= 25.t + ½.2.tdva
Zatímco žluté světlo trvá, řidič jede tímto způsobem:
x = 25,4 + ½.2.4dvam = 116 m
Ale 116 m je méně, než je dostupná vzdálenost k dalšímu rohu, což je 70 + 50 m = 120 m, proto nemůže projít celou ulici, dokud se nerozsvítí červené světlo. Doporučená akce je zabrzdit a zůstat 2 metry od semaforu.
Lidé zažívají účinky zrychlení na denní bázi: když cestují autem nebo autobusem, musí neustále brzdit a zrychlovat, aby přizpůsobili rychlost překážkám na silnici. Zrychlení se projeví také při jízdě nahoru nebo dolů ve výtahu.
Zábavní parky jsou místa, kde lidé platí za to, aby zažili účinky zrychlení a pobavili se.
V přírodě je rovnoměrně změněný přímočarý pohyb pozorován, když předmět spadne volně, nebo když je hozen svisle nahoru a čeká, až se vrátí na zem. Pokud je zanedbán odpor vzduchu, je hodnota zrychlení gravitační: 9,8 m / s2.
Zatím žádné komentáře