
Vysvětlení metody Gauss-Seidel, aplikace, příklady
The Gauss-Seidelova metoda je iterační postup k nalezení přibližného řešení systému lineárních algebraických rovnic s libovolně zvolenou přesností. Metoda se aplikuje na čtvercové matice s nenulovými prvky v jejich úhlopříčkách a konvergence je zaručena, pokud je matice diagonálně dominantní.
Vytvořil jej Carl Friedrich Gauss (1777-1855), který v roce 1823 předvedl soukromou demonstraci jednomu ze svých studentů. Později ho formálně publikoval Philipp Ludwig von Seidel (1821-1896) v roce 1874, odtud pochází jméno obou matematiků..
Pro úplné pochopení metody je nutné vědět, že matice je diagonálně dominantní, když je absolutní hodnota diagonálního prvku každé řady větší nebo rovna součtu absolutních hodnot ostatních prvků stejného řádku..
Matematicky je to vyjádřeno takto:
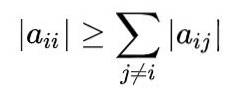
Rejstřík článků
- 1 Vysvětlení pomocí jednoduchého případu
- 1.1 Další kroky
- 1.2 Analýza metody
- 2 Aplikace
- 3 Příklady Gauss-Seidelovy metody
- 3.1 - Příklad 1
- 3.2 - Příklad 2
- 3.3 - Příklad 3
- 3.4 - Příklad 4
- 4 Odkazy
Vysvětlení pomocí jednoduchého případu
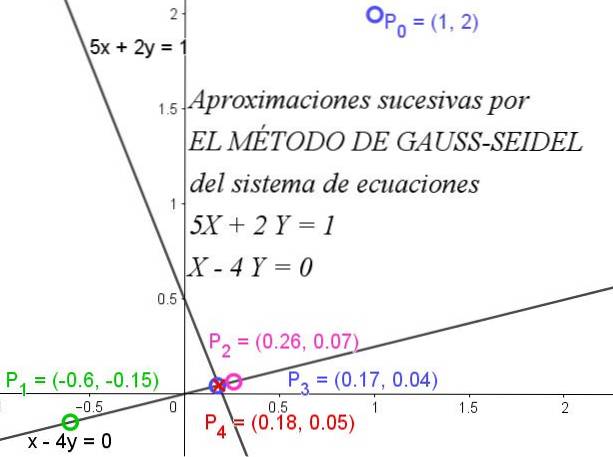
Abychom ilustrovali, z čeho se Gauss-Seidelova metoda skládá, vezmeme jednoduchý případ, ve kterém lze hodnoty X a Y nalézt v systému 2 × 2 lineárních rovnic zobrazených níže:
5X + 2Y = 1
X - 4Y = 0
Kroky, které je třeba následovat
1 - Nejprve je nutné určit, zda je konvergence bezpečná. Okamžitě je pozorováno, že se ve skutečnosti jedná o diagonálně dominantní systém, protože v prvním řádku má první koeficient vyšší absolutní hodnotu než ostatní v prvním řádku:
| 5 |> | 2 |
Druhý koeficient ve druhé řadě je také diagonálně dominantní:
| -4 |> | 1 |
dva- Proměnné X a Y jsou vyřešeny:
X = (1 - 2Y) / 5
Y = X / 4
3 - Umístí se libovolná počáteční hodnota, která se nazývá „seed“: Xo = 1, I = 2.
4-Začíná iterace: pro získání první aproximace X1, Y1 se v první rovnici kroku 2 nahradí zárodek a výsledek v druhé rovnici kroku 2:
X1 = (1 - 2 I) / 5 = (1 - 2 × 2) / 5 = -3/5
Y1 = X1 / 4 = (-3/5) / 4 = -3/20
5- Podobným způsobem postupujeme k získání druhé aproximace řešení soustavy rovnic:
X2 = (1 - 2 Y1) / 5 = (1 - 2x (-3/20)) / 5 = 13/50
Y2 = X2 / 4 = (13/50) / 4 = 13/200
6. Třetí iterace:
X3 = (1 - 2 Y2) / 5 = (1 - 2 (13/200)) / 5 = 87/500
Y3 = X3 / 4 = (87/500) / 4 = 87/2000
7- Čtvrtá iterace jako konečná iterace tohoto ilustrativního případu:
X4 = (1 - 2 Y3) / 5 = (1 - 2 (87/2000)) / 5 = 913/5000
Y4 = X4 / 4 = (913/5000) / 4 = 913/20000
Tyto hodnoty docela dobře souhlasí s řešením nalezeným jinými metodami řešení. Čtenář to může rychle zkontrolovat pomocí online matematického programu.
Analýza metody
Jak je vidět, v metodě Gauss-Seidel musí být přibližné hodnoty získané pro předchozí proměnnou ve stejném kroku nahrazeny následující proměnnou. Tím se odlišuje od jiných iteračních metod, jako je Jacobiho, u nichž každý krok vyžaduje aproximace předchozí fáze..
Metoda Gauss-Seidel není paralelní procedura, zatímco metoda Gauss-Jordan je. To je také důvod, že metoda Gauss-Seidel má rychlejší konvergenci - v méně krocích - než metoda Jordan..
Pokud jde o podmínku diagonálně dominantní matice, není to vždy splněno. Ve většině případů je však pro splnění podmínky dostatečné prosté zaměnění řádků z původního systému. Metoda dále konverguje téměř vždy, i když není splněna podmínka diagonální dominance..
Předchozí výsledek, získaný čtyřmi iteracemi metody Gauss-Seidel, lze zapsat v desítkové formě:
X4 = 0,1826
Y4 = 0,04565
Přesné řešení navrhovaného systému rovnic je:
X = 2/11 = 0,1818
Y = 1/22 = 0,04545.
Takže pouze se 4 iteracemi získáte výsledek s přesností na tisícinu (0,001).
Obrázek 1 ukazuje, jak postupné iterace rychle konvergují k přesnému řešení.
Aplikace
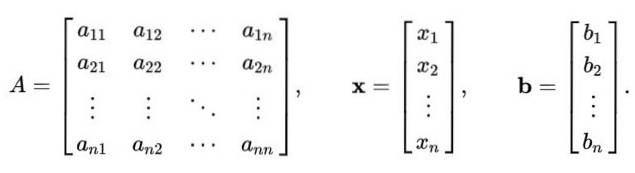
Metoda Gauss-Seidel se neomezuje pouze na systém lineárních rovnic 2 × 2. Výše uvedený postup lze zobecnit na řešení lineárního systému n rovnice s n neznámé, která je reprezentována v matici, jako je tato:
NA X = b
Kde NA je matice n x n, Zatímco X je vektor n složek n proměnných, které se mají vypočítat; Y b je vektor obsahující hodnoty nezávislých členů.
Zobecnit posloupnost iterací aplikovaných v ilustrativním případě na systém n x n, ze kterého se má vypočítat proměnná Xi, použije se následující vzorec:
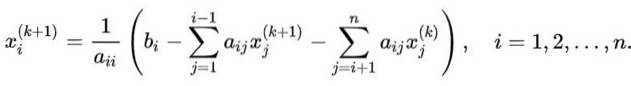
V této rovnici:
- k je index hodnoty získané v iteraci k.
-k + 1 označuje novou hodnotu v následujícím textu.
Konečný počet iterací je určen při hodnotě získané v iteraci k + 1 se liší od množství získaného bezprostředně před tím, o množství ε, což je přesně požadovaná přesnost.
Příklady Gauss-Seidelovy metody
- Příklad 1
Napište obecný algoritmus pro výpočet vektoru přibližných řešení X lineárního systému rovnic nxn, vzhledem k matici koeficientů NA, vektor nezávislých výrazů b, počet iterací (tjter) a počáteční nebo „počáteční“ hodnota vektoru X.
Řešení
Algoritmus se skládá ze dvou cyklů „To“, jednoho pro počet iterací a druhého pro počet proměnných. Bylo by to takto:
Pro k ∊ [1… iter]
Pro i ∊ [1… n]
X [i]: = (1 / A [i, i]) * (b [i] - ∑j = 1n(A [i, j] * X [j]) + A [i, i] * X [i])
- Příklad 2
Zkontrolujte funkčnost předchozího algoritmu jeho použitím v matematickém softwaru SMath Studio zdarma k použití, k dispozici pro Windows a Android. Vezměte si jako příklad případ matice 2 × 2, která nám pomohla ilustrovat Gauss-Seidelovu metodu.
Řešení

- Příklad 3
Aplikujte algoritmus Gauss-Seidel pro následující systém rovnic 3 × 3, který byl dříve uspořádán tak, aby byly dominantní koeficienty úhlopříčky (tj. Větší absolutní hodnota než absolutní hodnoty koeficientů stejného řádku):
9 X1 + 2 X2 - X3 = -2
7 X1 + 8 X2 + 5 X3 = 3
3 X1 + 4 X2 - 10 X3 = 6
Použijte nulový vektor jako semeno a zvažte pět iterací. Výsledek okomentujte.
Řešení
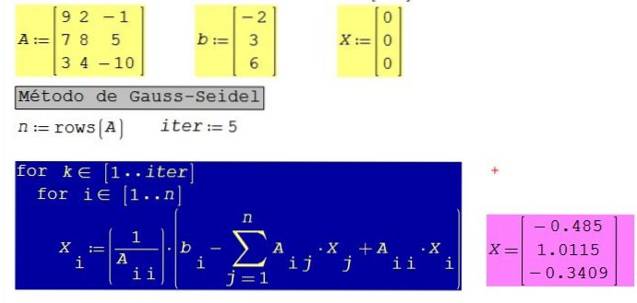
Pro stejný systém s 10 iteracemi namísto 5 jsou získány následující výsledky: X1 = -0,485; X2 = 1,0123; X3 = -0,3406
To nám říká, že k získání tří desetinných míst přesnosti stačí pět iterací a že metoda rychle konverguje k řešení.
- Příklad 4
Pomocí výše uvedeného algoritmu Gauss-Seidel najděte řešení systému rovnic 4 × 4 uvedených níže:
10 x1 - x2 + 2 x3 + 0 x4 = 6
-1 x1 + 11 x2 - 1 x3 + 3 x4 = 25
2 x1 - 1 x2 + 10 x3 - 1 x4 = -11
0 x1 + 3 x2 - 1 x3 + 8 x4 = 15
Chcete-li spustit metodu, použijte toto semeno:
x1 = 0, x2 = 0, x3 = 0 a x4 = 0
Zvažte 10 iterací a odhadněte chybu výsledku ve srovnání s iterací číslo 11.
Řešení

Při porovnání s další iterací (číslo 11) je výsledek identický. Největší rozdíly mezi těmito dvěma iteracemi jsou řádově 2 × 10-8, což znamená, že zobrazené řešení má přesnost nejméně sedm desetinných míst.
Reference
- Metody iteračního řešení. Gauss-Seidel. Obnoveno z: cimat.mx
- Numerické metody. Gauss-Seidel. Obnoveno z: test.cua.uam.mx
- Numerická: Gauss-Seidelova metoda. Obnoveno z: aprendeenlinea.udea.edu.co
- Wikipedia. Gauss-Seidelova metoda. Obnoveno z: en. wikipedia.com
- Wikipedia. Gauss-Seidelova metoda. Obnoveno z: es.wikipedia.com



Zatím žádné komentáře