The metoda rovnoběžníku je grafická metoda pro přidání dvou vektorů v rovině. Často se používá k nalezení výslednice dvou sil působících na tělo nebo dvou rychlostí, jako v případě plavce, který má v úmyslu překonat řeku kolmo a je vychýlen proudem.
K vytvoření rovnoběžníku se počátky vektorů, které se mají přidat, nakreslené v měřítku, musí shodovat v bodě.
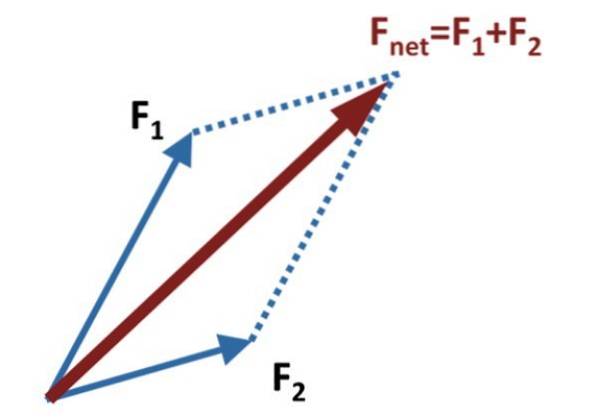
Potom jsou pomocné čáry nakresleny rovnoběžně s každým vektorem a dosáhnou konce druhého, jak je znázorněno na obrázku výše.
Součet nebo výsledný vektor, nazývaný také síla sítě, je vektor Fsíť, který se získá nakreslením vektoru, který vychází ze společného původu F1 Y Fdva, do bodu, kde se protínají pomocné rovnoběžky. V diagramu na obrázku jsou tyto znázorněny tečkovanými čarami.
Metoda získává svůj název podle obrázku, který je vytvořen pomocí vektorů sčítání a pomocných čar, což je přesně paralelogram. Hlavní úhlopříčka rovnoběžníku je součtový vektor.
Je velmi důležité si uvědomit, že pořadí, ve kterém jsou přidané vektory umístěny, vůbec nemění součet, protože tato operace mezi vektory je komutativní.
Rejstřík článků
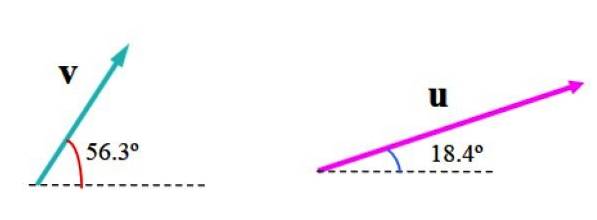
Následující obrázek ukazuje vektory proti Y nebo v libovolných jednotkách. Vektor proti měří 3,61 jednotek a svírá s horizontálou úhel 56,3 ° nebo měří 6,32 jednotek a úhel 18,4 ° vzhledem k uvedené referenční přímce.
Najdeme jeho vektorový součet pomocí metody rovnoběžníku.
Vyberte vhodné měřítko, například měřítko zobrazené na následujícím obrázku, ve kterém byla rovina rozdělena mřížkou. Šířka čtverce představuje jednu (1) jednotku.
Protože vektory nejsou při překladu změněny, jsou umístěny takovým způsobem, že jejich počátky se shodují s počátkem souřadnicového systému (obrázek vlevo).
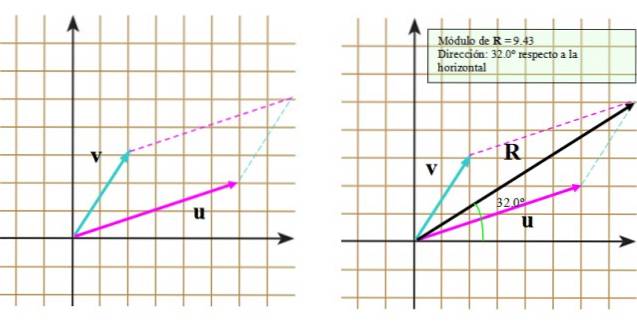
Nyní pojďme následovat tyto kroky:
Výsledek lze vidět na pravém obrázku, na kterém se objeví výsledný vektor R.
Pokud chceme znát velikost R, můžeme změřit jeho délku a porovnat ji s měřítkem, které máme. A pokud jde o jeho směr, lze jako reference použít například vodorovnou osu nebo svislou osu.
Při použití vodorovné osy nebo osy x úhel, který R tvar s uvedenou osou se měří úhloměrem a tímto způsobem známe směr R.
Podobně velikost a směr R lze vypočítat pomocí kosinových a sinusových vět, protože vytvořený rovnoběžník lze rozdělit na dva shodné trojúhelníky, jejichž strany jsou moduly vektorů nebo, proti Y R. Viz zpracovaný příklad 1.
Když jsou vektory navzájem kolmé, je vytvořeným obrazcem obdélník. Modul výsledného vektoru odpovídá délce úhlopříčky, kterou lze snadno vypočítat pomocí Pythagorovy věty.
Máme vektor proti, který měří 3,61 jednotek a svírá s horizontálou a vektorem úhel 56,3 ° nebo, jehož míra je 6,32 jednotek a svírá úhel 18,4 ° (obrázek 2). Určete modul výsledného vektoru R = nebo + proti a směr, který tvoří vektor s vodorovnou osou.
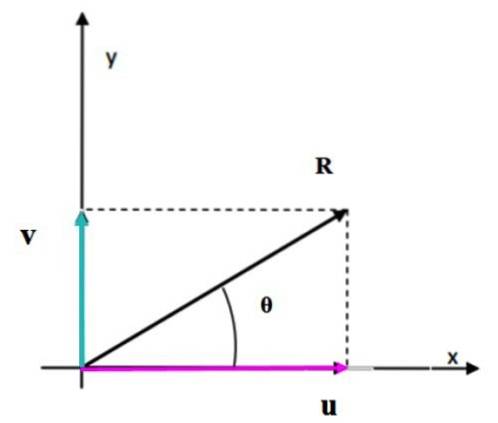
K získání vektoru je použita metoda rovnoběžníku podle výše popsaných kroků R. Jak již bylo řečeno, pokud jsou vektory pečlivě kresleny podle měřítka a pomocí pravítka a úhloměru, velikost a směr R se měří přímo na výkresu.
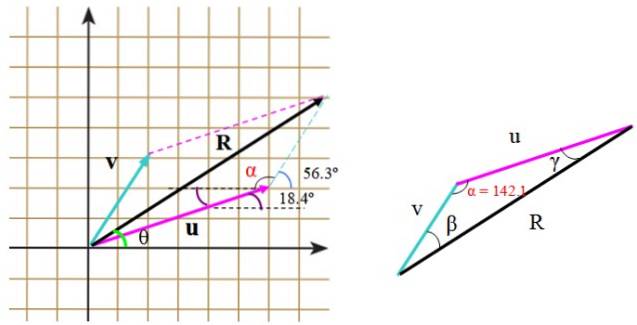
Mohou být také vypočítány přímo pomocí trigonometrie a vlastností úhlů. Když vytvořený trojúhelník není správný, jako v tomto případě, kosinová věta se použije k nalezení chybějící strany.
V pravoúhlém trojúhelníku strany měří u, v a R. K použití kosinové věty je nutné znát úhel mezi proti Y nebo, které můžeme najít pomocí mřížky, vhodně umístit úhly poskytované příkazem.
Tento úhel je α a skládá se z:
α = (90-56,3 °) + 90 ° + 18,4 ° = 142,1 °
Podle kosinové věty:
Rdva = vdva + nebodva - 2u⋅v⋅cos α = 3,61dva + 6.32dva - 2 × 3,61 × 6,32 × cos 142,1 ° = 88,98
R = 9,43 jednotek.
Nakonec úhel mezi R a vodorovná osa je θ = 18,4 ° + γ. Úhel γ lze zjistit pomocí sinusové věty:
sin α / R = sin γ / u
Proto:
sin γ = v (sin α / R) = 3,61 x (sin 142,1 ° / 9,43)
γ = 13,6 °
θ = 18,4 ° + 13,6 ° = 32 °
Plavec se chystá překonat řeku plavou kolmo na proud konstantní rychlostí 2,0 m / s. Plavec začíná od A, ale končí v B, bodě po proudu, kvůli proudu, který ho odklonil.
Pokud je rychlost proudu 0,8 m / s a všechny rychlosti jsou považovány za konstantní, najděte rychlost plavce, jak ji vidí pozorovatel stojící na břehu.
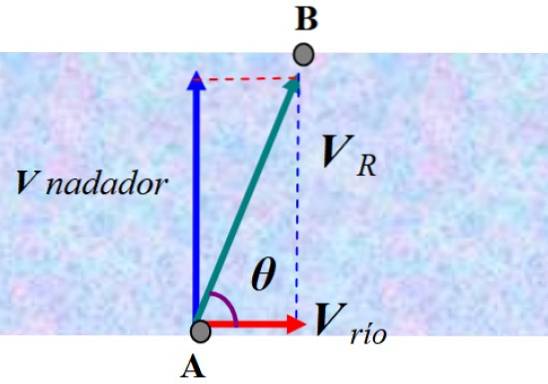
Pozorovatel stojící na břehu by viděl, jak je plavec vychýlen podle výsledné rychlosti PROTIR. Abychom našli odpověď, musíme vektorově přidat rychlost plavce vzhledem k vodě a rychlost proudu, kterou nazýváme PROTI Řeka:
PROTI R = PROTI plavec + PROTI Řeka
Na obrázku, který nemá měřítko, byly vektory přidány k získání PROTI R. V tomto případě lze Pythagorovu větu použít k získání její velikosti:
PROTIRdva = 2,0dva + 0,8dva = 4,64
PROTIR = 2,15 m / s
Směr, ve kterém se plavec odchyluje od kolmého směru, lze snadno vypočítat s tím, že:
θ = arctg (2 / 0,8) = 68,2 °
Poté se plavec odchýlí od svého původního směru o 90 ° - 68,2 ° = 27,2 °.
Zatím žádné komentáře