
Napsaný úhel definice kružnice, věty, příklady
The vepsaný úhel kruhu Je to ten, který má svůj vrchol na obvodu a jeho paprsky jsou k němu šikmé nebo tečné. V důsledku toho bude vepsaný úhel vždy konvexní nebo plochý..
Na obrázku 1 je znázorněno několik úhlů zapsaných v jejich příslušných obvodech. Úhel ∠EDF je zapsán tím, že jeho vrchol D na obvodu a jeho dva paprsky [DE) a [DF) protínající obvod.
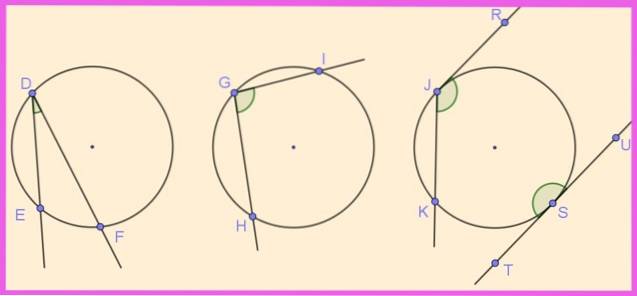
Podobně je vepsán úhel ∠HGI, který má svůj vrchol na obvodu a jeho strany se k němu sešikují.
Úhly ∠KJR a ∠UST jsou také zapsány na obvodu. První má sečnu a druhou tečnu, zatímco druhá má své dvě strany tečné k obvodu, tvořící rovinu vepsaného úhlu (180 °).
Někteří autoři nazývají částečně vepsaný úhel, který má jedna z jeho stran tečna k obvodu, ale v tomto článku je považován za vepsaný..
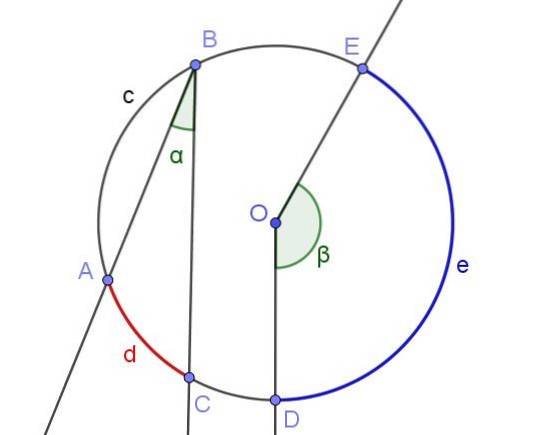
Každý vepsaný úhel definuje nebo subtenduje oblouk s ním spojený. Například na obrázku 2 je vepsaný úhel ∠ABC úměrný oblouku A⌒C délky d.
Stejný obrázek ukazuje úhel ∠DOE, který není vepsán do obvodu, protože jeho vrchol nemá svůj obvod, ale ve středu O.
Rejstřík článků
- 1 Středový úhel
- 2 věty
- 2.1 - Věta 1 (vepsaný úhel a středový úhel)
- 2.2 - Věta 2
- 2.3 - Věta 3
- 3 příklady
- 3.1 - Příklad 1
- 3.2 - Příklad 2
- 4 Odkazy
Středový úhel
Kromě zapsaného úhlu, v obvodu středový úhel, což je ten, jehož vrchol je ve středu obvodu a jehož strany protínají obvod.
Míra v radiánech středního úhlu je kvocient mezi subtending obloukem, to znamená obloukem obvodu mezi stranami úhlu a poloměrem obvodu.
Pokud je obvod jednotný (poloměr 1), pak délka oblouku ve stejných jednotkách poloměru je mírou úhlu v radiánech.
A když je požadována míra úhlu ve stupních, pak je míra v radiánech vynásobena faktorem 180 ° / π.
Přístroje pro měření úhlů vždy používají středový úhel a délka oblouku jím podřízeného je přímo kalibrována ve stupních. To znamená, že kdykoli se měří úhel, měří se v pozadí délka oblouku, která je podřízena středním úhlem.
Věty
- Věta 1 (vepsaný úhel a střední úhel)
Míra zapsaného úhlu je polovinou míry středového úhlu, pokud oba úhly mají stejný oblouk.
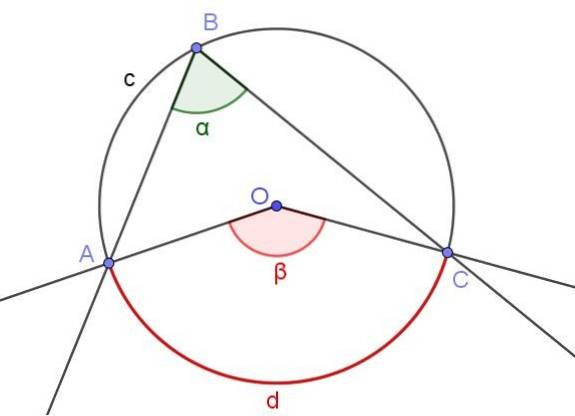
Na obrázku 4 jsou znázorněny dva úhly ∠ABC a ∠AOC, které protínají stejný oblouk obvodu A⌒C.
Pokud je míra vepsaného úhlu α, pak míra β středního úhlu je dvojnásobkem míry vepsaného úhlu (β = 2 α), protože obě mají stejný oblouk míry d.
Demonstrace 1a
Abychom dokázali větu 1, začneme ukázáním několika konkrétních případů, dokud se nedostaneme k obecnému případu.
Předpokládejme vepsaný úhel, ve kterém jedna z jeho stran prochází středem obvodu, jak je znázorněno na obrázku 5.
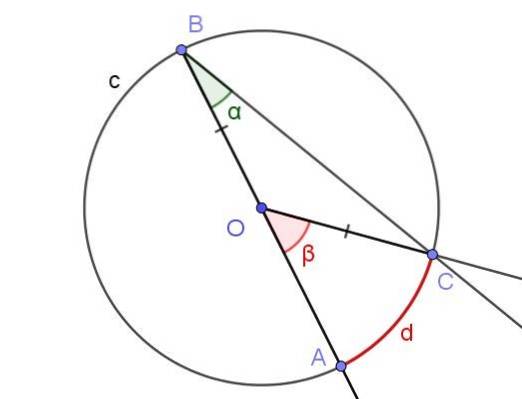
V tomto případě se vytvoří rovnoramenný trojúhelník COB, protože [OC] = [OB].
V rovnoramenném trojúhelníku jsou úhly sousedící se základnou stejné, proto ∠BCO = ∠ABC = α. Na druhé straně ∠COB = 180º - β.
Vzhledem k součtu vnitřních úhlů trojúhelníku COB máme:
α + α + (180 ° - β) = 180 °
Z čehož vyplývá, že 2 α = β, nebo co je ekvivalentní: α = β / 2. To se shoduje s tím, co uvádí věta 1: míra vepsaného úhlu je polovina středního úhlu, pokud oba úhly mají stejný akord [AC].
Demonstrace 1b
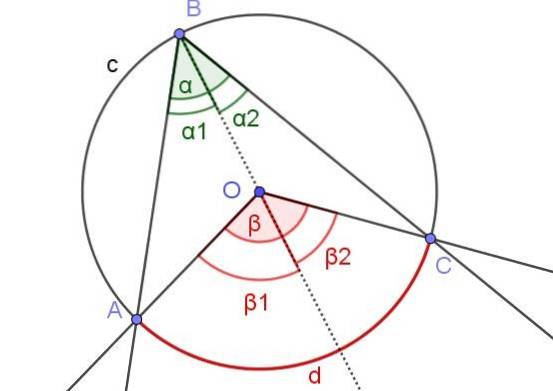
V tomto případě máme vepsaný úhel ∠ABC, ve kterém je střed O obvodu v úhlu.
K prokázání věty 1 je v tomto případě nakreslen pomocný paprsek [BO), takže máme dva zapsané úhly ∠ABO a ∠OBC sousedící s uvedeným paprskem.
Podobně máme středové úhly β1 a βdva sousedící s uvedeným paprskem. Tímto způsobem máme stejnou situaci jako v důkazu 1a, takže lze konstatovat, že αdva = βdva / 2 a α1 = β1 /dva. Protože α = α1 + αdva a β = β1 + βdva z toho tedy vyplývá, že α = α1 + αdva = β1 / 2 + βdva / 2 = (β1 + βdva) / 2 = β / 2.
Na závěr α = β / 2, který splňuje větu 1.
- Věta 2
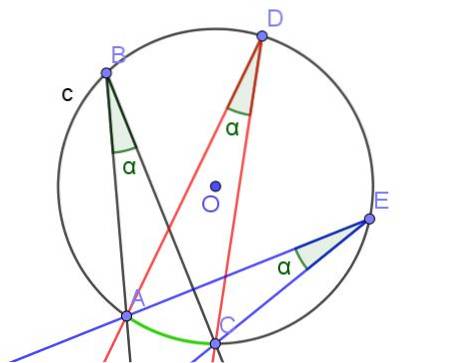
Pokud dva nebo více vepsaných úhlů svírá stejný oblouk, pak mají stejnou míru.
- Věta 3
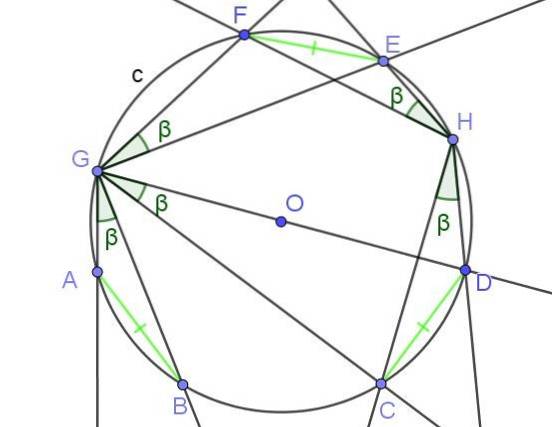
Vepsané úhly, které podstupují akordy stejné míry, jsou stejné.
Příklady
- Příklad 1
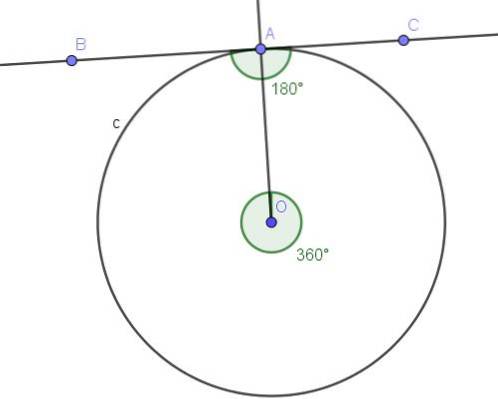
Ukažte, že vepsaný úhel, který tvoří průměr, je pravý úhel.
Řešení
Středový úhel ∠AOB spojený s průměrem je rovinný úhel, jehož míra je 180 °.
Podle věty 1 má každý úhel zapsaný v obvodu, který svírá stejný akord (v tomto případě průměr), jako měřítko polovinu středního úhlu, který svírá stejný akord, což je pro náš příklad 180 ° / 2 = 90 °.
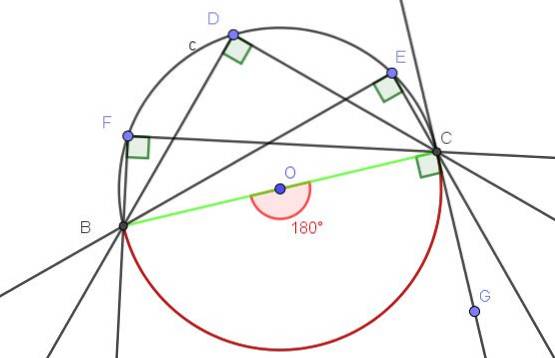
- Příklad 2
Přímka (BC) tečna A k obvodu C určuje vepsaný úhel ∠BAC (viz obrázek 10).
Ověřte, že věta 1 o zapsaných úhlech je splněna.
Řešení
Úhel ∠BAC je vepsaný, protože jeho vrchol je na obvodu a jeho strany [AB) a [AC) jsou tečné k obvodu, takže definice vepsaného úhlu je splněna.
Napsaný úhel ∠BAC na druhé straně obepíná oblouk A, A, což je celý obvod. Středový úhel, který svírá oblouk A⌒A, je konvexní úhel, jehož měřítkem je plný úhel (360 °).
Vepsaný úhel, který svírá celý oblouk, měří polovinu příslušného středového úhlu, tj. ∠BAC = 360 ° / 2 = 180 °.
Se všemi výše uvedenými skutečnostmi je ověřeno, že tento konkrétní případ splňuje větu 1.
Reference
- Baldor. (1973). Geometrie a trigonometrie. Středoamerický kulturní úvodník.
- E. A. (2003). Prvky geometrie: s cvičeními a geometrií kompasu. University of Medellin.
- Geometrie 1. ESO. Úhly na obvodu. Obnoveno z: edu.xunta.es/
- Celá věda. Navrhovaná cvičení úhlů v obvodu. Obnoveno z: francesphysics.blogspot.com
- Wikipedia. Vepsaný úhel. Obnoveno z: es.wikipedia.com



Zatím žádné komentáře