
Definice a charakteristika nulového úhlu, příklady, cvičení
The nulový úhel Je to ten, jehož míra je 0, a to jak ve stupních, tak v radiánech, nebo jiný systém měření úhlu. Proto postrádá šířku nebo otevírání, jako například mezi dvěma rovnoběžnými čarami..
Ačkoli jeho definice zní dostatečně jednoduše, nulový úhel je velmi užitečný v mnoha fyzikálních a inženýrských aplikacích, stejně jako v navigaci a designu..
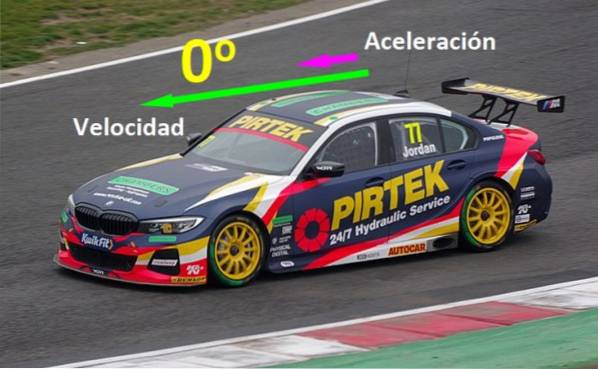
Existují fyzické veličiny, které je třeba paralelně zarovnat, aby se dosáhlo určitých účinků: pokud se auto pohybuje po dálnici po přímce a zadává svůj vektor rychlosti proti a jeho vektor zrychlení na tam je 0 °, auto se pohybuje rychleji a rychleji, ale pokud auto brzdí, jeho zrychlení je opačné než jeho rychlost (viz obrázek 1).
Následující obrázek ukazuje různé typy úhlů včetně nulového úhlu doprava. Jak je vidět, 0 ° úhlu chybí šířka nebo otevření..

Rejstřík článků
- 1 Příklady nulových úhlů
- 1.1 - Účinky nulového úhlu na fyzikální veličiny
- 2 Cvičení
- 2.1 - Cvičení 1
- 2.2 - Cvičení 2
- 3 Odkazy
Příklady nulových úhlů
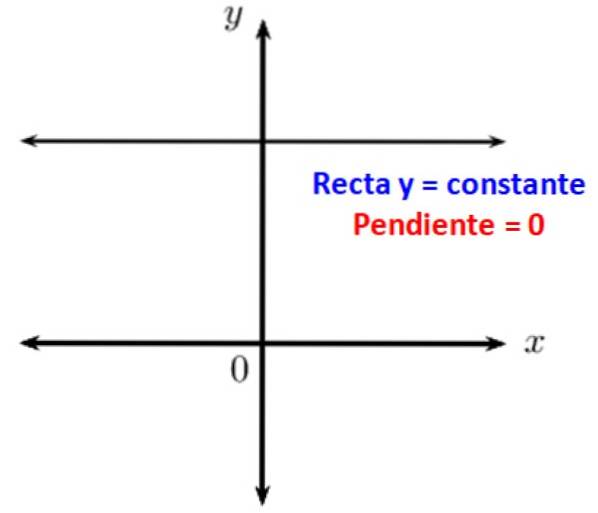
Je známo, že paralelní linie navzájem tvoří nulový úhel. Když máte vodorovnou čáru, je rovnoběžná s osou x kartézského souřadného systému, proto její sklon vzhledem k ní je 0. Jinými slovy, vodorovné čáry mají nulový sklon.
Také trigonometrické poměry nulového úhlu jsou 0, 1 nebo nekonečno. Proto je nulový úhel přítomen v mnoha fyzických situacích, které zahrnují operace s vektory. Jsou to tyto důvody:
-hřích 0º = 0
-cos 0º = 1
-tg 0º = 0
-s 0 ° = 1
-cosec 0º → ∞
-ctg 0º → ∞
A budou užitečné analyzovat některé příklady situací, ve kterých přítomnost nulového úhlu hraje zásadní roli:
- Účinky nulového úhlu na fyzikální veličiny
Vektorové přidání
Jsou-li dva vektory rovnoběžné, je úhel mezi nimi nulový, jak je vidět na obrázku 4a výše. V tomto případě je součet obou proveden umístěním jeden po druhém a velikost vektoru součtu je součtem velikostí sčítání (obrázek 4b).

Jsou-li dva vektory rovnoběžné, je úhel mezi nimi nulový, jak je vidět na obrázku 4a výše. V tomto případě je součet obou proveden umístěním jeden po druhém a velikost vektoru součtu je součtem velikostí sčítání (obrázek 4b)
Točivý moment nebo točivý moment
Točivý moment nebo točivý moment způsobuje rotaci těla. Závisí to na velikosti aplikované síly a na tom, jak je aplikována. Velmi reprezentativním příkladem je klíč na obrázku.
K dosažení nejlepšího efektu otáčení je síla aplikována kolmo na rukojeť klíče, a to buď nahoru nebo dolů, ale neočekává se žádné otáčení, pokud je síla rovnoběžná s rukojetí..
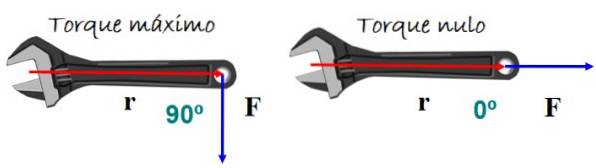
Matematicky točivý moment τ je definován jako křížový produkt nebo křížový produkt mezi vektory r (vektor polohy) a F (vektor síly) z obrázku 5:
τ = r X F
Velikost točivého momentu je:
τ = r F sin θ
Kde θ je úhel mezi r Y F. Když sin θ = 0 je točivý moment nulový, v tomto případě θ = 0 ° (nebo také 180 °).
Tok elektrického pole
Tok elektrického pole je skalární velikost, která závisí na intenzitě elektrického pole a také na orientaci povrchu, kterým prochází..
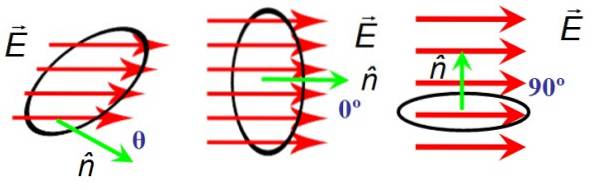
Na obrázku 6 je kruhový povrch oblasti A, kterým procházejí čáry elektrického pole A. Orientace povrchu je dána normálovým vektorem n. Vlevo pole a normálový vektor tvoří libovolný ostrý úhel θ, ve středu navzájem vytvářejí nulový úhel a vpravo jsou kolmé.
Když A Y n jsou kolmé, siločáry neprotínají povrch, a proto je tok nulový, zatímco když je úhel mezi A Y n je null, čáry zcela procházejí povrchem.
Označení toku elektrického pole řeckým písmenem Φ (čtěte „fi“), jeho definice jednotného pole jako na obrázku, vypadá takto:
Φ = A•nNA
Bod uprostřed obou vektorů označuje bodový součin nebo součin bodů, který je alternativně definován následovně:
Φ = A•nA = EAcosθ
Tučně a šipky nad písmenem jsou prostředky k rozlišení mezi vektorem a jeho velikostí, která je označena běžnými písmeny. Protože cos 0 = 1, je tok maximální, když A Y n jsou paralelní.
Výcvik
- Cvičení 1
Dvě síly P Y Q působí současně na bodový objekt X, obě síly zpočátku mezi nimi tvoří úhel θ. Co se stane s velikostí výsledné síly, když θ klesne na nulu?
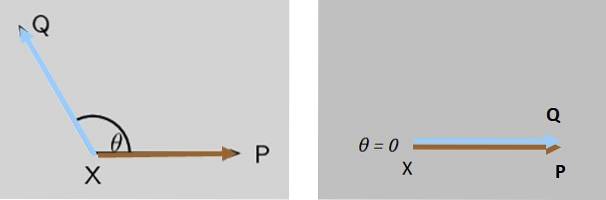
Řešení
Velikost výsledné síly Q + P postupně se zvyšuje, dokud není maximální, když Q Y P jsou zcela paralelní (obrázek 7 vpravo).
- Cvičení 2
Uveďte, zda je nulový úhel řešením následující trigonometrické rovnice:
cos 2x = 1 + 4 sin x
Řešení
Trigonometrická rovnice je rovnice, ve které je neznámá součástí argumentu trigonometrického poměru. K vyřešení navrhované rovnice je vhodné použít vzorec pro kosinus dvojitého úhlu:
cos 2x = cosdva x - hříchdva X
Protože tímto způsobem se stává argument na levé straně X namísto 2x. Pak:
cosdva x - hříchdva x = 1 + 4sin x
Na druhou stranu cosdva x + hříchdva x = 1, takže:
cosdva x - hříchdva x = cosdva x + hříchdva x + 4sen x
Termín cosdva x je zrušeno a zůstává:
- sendva x = hříchdva x + 4sen x → - 2sendva x - 4senx = 0 → 2sendva x + 4senx = 0
Nyní je provedena následující změna proměnné: sinx = u a rovnice se stane:
2udva + 4u = 0
2u (u + 4) = 0
Čí řešení jsou: u = 0 a u = -4. Po vrácení změny bychom měli dvě možnosti: sin x = 0 a sinx = -4. Toto poslední řešení není životaschopné, protože sinus libovolného úhlu je mezi -1 a 1, takže nám zbývá první alternativa:
sin x = 0
X = 0º je tedy řešení, ale funguje také jakýkoli úhel, jehož sinus je 0, což může být také 180 ° (π radiány), 360 ° (2 π radiány) a také příslušné negativy.
Nejobecnějším řešením trigonometrické rovnice je: x = kπ, kde k = 0, ± 1, ± 2, ± 3,…. k celé číslo.
Reference
- Baldor, A. 2004. Geometrie roviny a prostoru pomocí trigonometrie. Publicaciones Cultural S.A. de C.V. Mexiko.
- Figueroa, D. (2005). Série: Fyzika pro vědu a techniku. Svazek 3. Systémy částic. Upravil Douglas Figueroa (USB).
- Figueroa, D. (2005). Série: Fyzika pro vědu a techniku. Svazek 5. Elektrické interakce. Upravil Douglas Figueroa (USB).
- OnlineMathLearning. Druhy úhlů. Obnoveno z: onlinemathlearning.com.
- Zill, D. 2012. Algebra, trigonometrie a analytická geometrie. McGraw Hill Interamericana.



Zatím žádné komentáře