The složená čísla jsou celá čísla, která mají více než dva dělitele. Podíváme-li se pozorně, všechna čísla jsou přinejmenším dělitelná přesně podle sebe a podle 1. Těch, která mají pouze tyto dva dělitele, se říká prvočísla a ta, která mají více, jsou sloučeniny..
Podívejme se na číslo 2, které lze rozdělit pouze na 1 a 2. Číslo 3 má také dva dělitele: 1 a 3. Proto jsou oba prvočísla. Nyní se podívejme na číslo 12, které můžeme rozdělit přesně na 2, 3, 4, 6 a 12. Když máme 5 dělitelů, 12 je složené číslo.
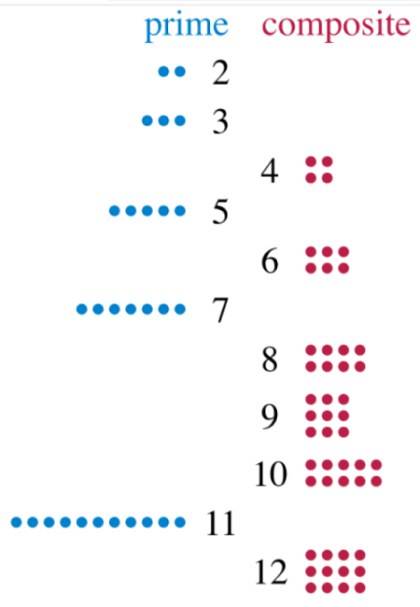
A co se stane s číslem 1, které rozděluje všechny ostatní? Není to primární, protože nemá dva dělitele a není složené, proto 1 nespadá do žádné z těchto dvou kategorií. Existuje ale mnohem více čísel..
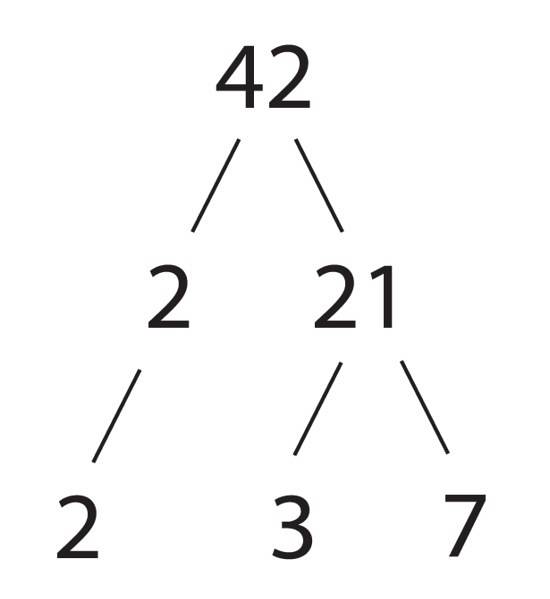
Složená čísla lze vyjádřit jako součin prvočísel a tento součin, s výjimkou pořadí faktorů, je pro každé číslo jedinečný. To je zajištěno základní větou aritmetiky, kterou prokázal řecký matematik Euklid (325–365 př. N. L.).
Vraťme se k číslu 12, které můžeme vyjádřit různými způsoby. Zkusme některé:
12 = 4 x 3 = 2 x 6 = 12 x 1 = 2dva x 3 = 3 x 2dva = 3 x 2 x 2 = 2 x 2 x 3 = 2 x 3 x 2
Tvary, které jsou zvýrazněny tučně, jsou produkty prvočísel a jediná věc, která se mění, je pořadí faktorů, o kterých víme, že produkt nezmění. Ostatní formy, i když jsou platné pro vyjádření 12, nespočívají pouze v prvočíslech.
Pokud chceme rozložit složené číslo na jeho prvočísla, musíme ho rozdělit mezi prvočísla tak, aby dělení bylo přesné, to znamená, že zbytek je 0.
Tento postup se nazývá Prvočíselný rozklad nebo kanonický rozklad. Prime faktory lze zvýšit na pozitivní exponenty.
Rozložíme číslo 570 s tím, že je sudé a tedy dělitelné 2, což je prvočíslo.
Použijeme lomítko k oddělení čísla nalevo od rozdělovačů napravo. Příslušné kvocienty jsou umístěny pod číslo, jak jsou získány. Rozklad je dokončen, když je poslední číslice v levém sloupci 1:
570 │2
285 │
Když vydělíme 2, kvocient je 285, což je dělitelné 5, další prvočíslo končící 5.
570 │2
285 │5
57 │
57 je dělitelné 3, také prvočíslo, protože součet jeho číslic 5 + 7 = 12 je násobkem 3.
570 │2
285 5
57 3
19 │
Nakonec dostaneme 19, což je prvočíslo, jehož dělitele jsou 19 a 1:
570 │2
285 5
57 3
19-19
1 │
Získáním 1 již můžeme vyjádřit 570 tímto způsobem:
570 = 2 x 5 x 3 x 19
A vidíme, že ve skutečnosti jde o produkt 4 prvočísel.
V tomto příkladu začneme vydělením 2, ale stejné faktory (v jiném pořadí) by byly získány, kdybychom začali vydělením například 5.
Chcete-li rozložit složené číslo na jeho hlavní faktory, je nutné ho přesně rozdělit. Kritéria dělitelnosti mezi prvočísly jsou pravidla, která umožňují zjistit, kdy je číslo dělitelné přesně jiným, aniž byste museli zkoušet nebo dokazovat.
Všechna sudá čísla, ta, která končí 0, nebo sudá čísla, jsou dělitelná 2.
Pokud je součet číslic čísla násobkem 3, pak je číslo také dělitelné 3.
Čísla končící na 0 nebo 5 jsou dělitelná 5.
Číslo je dělitelné 7, pokud při oddělení poslední číslice, vynásobení 2 a odečtení zbývajícího čísla, je výsledná hodnota násobkem 7.
Toto pravidlo se zdá být trochu komplikovanější než předchozí, ale ve skutečnosti to není tak moc, podívejme se tedy na příklad: bude 98 dělitelné 7?
Postupujme podle pokynů: oddělíme poslední číslici, která je 8, vynásobíme ji 2, což dá 16. Číslo, které zůstane při oddělení 8, je 9. Odečteme 16 - 9 = 7. A protože 7 je násobkem sebe sama , 98 je dělitelný mezi 7.
Pokud se součet čísel v sudé poloze (2, 4, 6…) odečte od součtu čísel v liché poloze (1, 3, 5, 7…) a získá se 0 nebo násobek 11, počet je dělitelné 11.
První násobky 11 lze snadno identifikovat: jsou to 11, 22, 33, 44… 99. Ale pozor, 111 není, místo toho 110 je.
Jako příklad se podívejme, jestli je 143 násobkem 11.
Toto číslo má 3 číslice, jediná sudá číslice je 4 (druhá), dvě liché číslice jsou 1 a 3 (první a třetí) a jejich součet je 4.
Odečtou se oba součty: 4 - 4 = 0 a protože se získá 0, ukazuje se, že 143 je násobkem 11.
Číslo bez jedné číslice musí být odečteno od 9násobku této číslice. Pokud počet vrátí 0 nebo násobek 13, je číslo násobkem 13.
Jako příklad si ověříme, že 156 je násobkem 13. Jednicová číslice je 6 a číslo, které zůstane bez ní, je 15. Vynásobíme 6 x 9 = 54 a nyní odečteme 54 - 15 = 39.
Ale 39 je 3 x 13, takže 56 je násobkem 13.
Dvě nebo více prvočísel nebo složená čísla mohou být prvočísla nebo ko-prvočísla. To znamená, že jediný společný dělitel, kterého mají, je 1.
Pokud jde o trestné činy, musíte si pamatovat dvě důležité vlastnosti:
-Dvě, tři a více po sobě jdoucích čísel jsou vždy navzájem prvočísla.
-Totéž lze říci o dvou, třech nebo více po sobě jdoucích lichých číslech.
Například 15, 16 a 17 jsou navzájem prvočísla, stejně tak 15, 17 a 19.
Prvočíslo má dva dělitele, stejné číslo a 1. A kolik dělitelů má složené číslo? Mohou to být bratranci nebo sloučeniny.
Nechť N je složené číslo vyjádřené kanonickým rozkladem takto:
N = an . bm. Cp... rk
Kde a, b, c… r jsou hlavní faktory a n, m, p… k příslušné exponenty. Počet dělitelů C, který má N, je dán vztahem:
C = (n +1) (m + 1) (p +1) ... (k + 1)
S C = primární dělitele + složené dělitele + 1
Například 570, který je vyjádřen takto:
570 = 2 x 5 x 3 x 19
Všechny hlavní faktory se zvýší na 1, proto 570 má:
C = (1 + 1) (1 + 1) (1+ 1) (1 +1) = 16 dělitelů
Z těchto 10 dělitelů již víme: 1, 2, 3, 5, 19 a 570. Chybí ještě 10 dělitelů, což jsou složená čísla: 6, 10, 15, 30, 38, 57, 95, 114, 190 a 285. Jsou objeveny pozorováním rozkladu na primární faktory a také násobením kombinací těchto faktorů dohromady..
Rozložte následující čísla na hlavní faktory:
a) 98
b) 143
c) 540
d) 3705
98 │2
49 │7
7 │7
1 │
98 = 2 x 7 x 7
143 11
13-13
1 │
143 = 11 x 13
540 │5
108 │2
54 │2
27 │3
9 │3
3 │3
1 │
540 = 5 x 2 x 2 x 3 x 3 x 3 = 5 x 2dva x 33
3705 5
741 │3
247 13
19-19
1 │
3705 = 5 x 3 x 13 x 19
Zjistěte, zda jsou následující čísla navzájem prvočísla:
6, 14, 9
-Děliteli 6 jsou: 1, 2, 3, 6
-Pokud jde o 14, je to dělitelné: 1, 2, 7, 14
-Nakonec má 9 dělitele: 1, 3, 9
Jediný dělitel, kterého mají společného, je 1, a proto jsou navzájem hlavní.
Zatím žádné komentáře