
Kvantová čísla, k čemu jsou a k čemu jsou

The nkvantová čísla se používají k popisu kvantového stavu elektronů v atomu a pocházejí z řešení Schrödingerovy rovnice pro nejjednodušší ze všech: vodík.
Schrödingerova rovnice je diferenciální rovnice, jejíž řešení je vlnové funkce a jsou označeny řeckým písmenem ψ. Lze navrhnout nekonečná řešení a jejich čtverec se rovná pravděpodobnosti nalezení elektronu v malé oblasti vesmíru, tzv. orbitální.
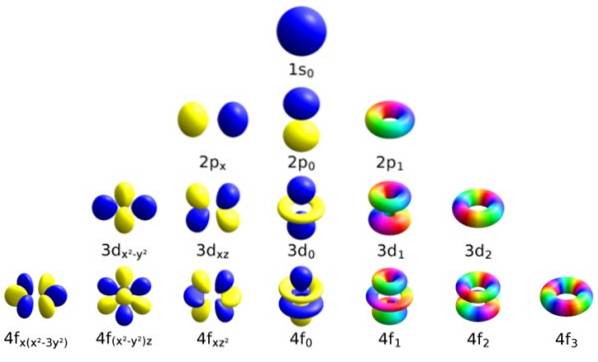
Každý orbitál má určité charakteristiky, které jej odlišují od ostatních, jako je energie, moment hybnosti a spin, zcela kvantová vlastnost elektronu a která je mimo jiné zodpovědná za magnetické efekty..
Způsob, jak identifikovat každou oběžnou dráhu, je odlišit ji množinou čísel, která ji popisují, a to jsou přesně ta kvantová čísla:
-n: je hlavní kvantové číslo.
-ℓ: azimutální kvantové číslo.
-mℓ, je magnetické číslo.
-ms, číslo rotace.
Rejstřík článků
- 1 K čemu jsou kvantová čísla?
- 1.1 Vlnové funkce
- 2 Co jsou to kvantová čísla?
- 2.1 Hlavní kvantové číslo
- 2.2 Kvantové číslo azimutálního nebo úhlového momentu
- 2.3 Magnetické kvantové číslo mℓ
- 2.4 Spinové kvantové číslo ms
- 3 Odkazy
K čemu jsou kvantová čísla?
Kvantová čísla se používají k popisu stavu elektronů uvnitř atomu. Ten atomový model, ve kterém se elektron točí kolem jádra, je nepřesný, protože není v souladu s atomovou stabilitou nebo s velkým počtem pozorovaných fyzikálních jevů.
Proto dánský Niels Bohr (1885-1962) předložil v roce 1913 odvážný návrh: elektron lze nalézt pouze na určitých stabilních drahách, jejichž velikost závisí na celé číslo zvané n.
Později, v roce 1925, také rakouský fyzik Erwin Schrödinger (1887-1961) navrhl diferenciální rovnici v parciálních derivacích, jejichž řešení popisují atom vodíku. Jsou to vlnové funkce ψ zmíněné na začátku.
Tato diferenciální rovnice zahrnuje tři prostorové souřadnice plus čas, ale pokud to není zahrnuto, řešení Schrödingerovy rovnice je analogické řešení stojaté vlny (vlna, která se šíří mezi určitými limity).
Vlnové funkce
Časově nezávislá Schrödingerova rovnice je řešena ve sférických souřadnicích a řešení je zapsáno jako součin tří funkcí, jedné pro každou prostorovou proměnnou. V tomto souřadnicovém systému namísto použití souřadnic kartézských os X, Y Y z jsou použity souřadnice r, θ Y φ. Takto:
ψ (r, θ, φ) = R (r) ⋅f (θ) ⋅g (φ)
Vlnová funkce je nehmotná, avšak kvantová mechanika nám říká, že čtvercová amplituda:
| ψ (r, θ, φ) |dva
To znamená, že modul nebo absolutní hodnota vlnové funkce, na druhou, je reálné číslo, které představuje pravděpodobnost nalezení elektronu v určité oblasti kolem bodu, jehož souřadnice jsou r, θ Y φ.
A tato skutečnost je něco konkrétnějšího a hmatatelnějšího.
Chcete-li najít vlnovou funkci, musíte vyřešit tři obyčejné diferenciální rovnice, jednu pro každou proměnnou r, θ Y φ.
Řešení každé rovnice, kterou budou funkce R (r), f (θ) ag (φ), obsahují první tři zmíněná kvantová čísla.
Co jsou to kvantová čísla?
Níže stručně popíšeme povahu každého kvantového čísla. První tři, jak již bylo uvedeno, vznikají z řešení Schrödingerovy rovnice.
Čtvrté číslo přidal Paul Dirac (1902 - 1984) v roce 1928.
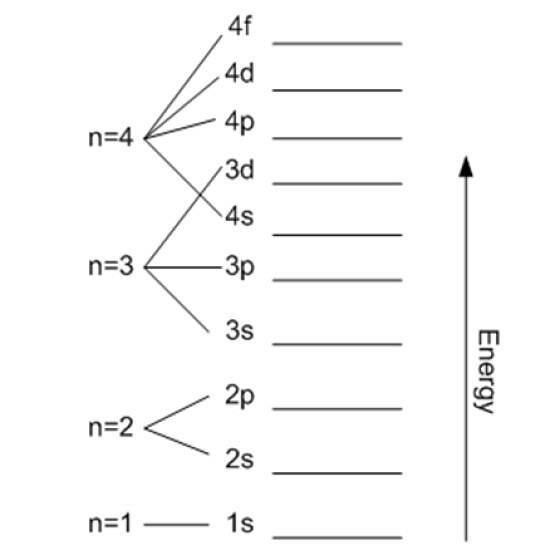
Hlavní kvantové číslo
Označuje to n a označuje velikost povoleného orbitu, stejně jako energii elektronu. Čím vyšší je jeho hodnota, tím dále je elektron od jádra a jeho energie bude také vyšší, ale na oplátku snižuje jeho stabilitu.
Toto číslo vyplývá z funkce R (r), což je pravděpodobnost nalezení elektronu v určité vzdálenosti r jádra, které je určeno:
-Planckova konstanta: h = 6,626 × 10 -3. 4 J.s
-Hmotnost elektronu ma = 9,1 × 10-31 kg
-Elektronový náboj: e = 1,6 × 10-19 C.
-Elektrostatická konstanta: k = 9 × 10 9 N.mdva/ C.dva
Když n = 1, odpovídá Bohrovu poloměru, který je přibližně 5,3 × 10-11 m.
S výjimkou první vrstvy se ostatní dělí na dílčí vrstvy nebo podúrovně. Každá skořápka má energii ve voltech elektronů danou:

- K (n = 1)
- L (n = 2)
- M (n = 3)
- N (n = 4)
- O (n = 5)
- P (n = 6)
- Q (n = 7).
Teoreticky neexistuje žádná horní mez pro n, ale v praxi se pozoruje, že dosahuje pouze n = 8. Nejnižší možná energie odpovídá n = 1 a je to základní stav.
Azimutální nebo kvantové číslo momentu hybnosti
Označeno kurzívou ℓ, toto číslo určuje tvar orbitalů kvantifikací velikosti orbitálního momentu hybnosti elektronu.
Může nabývat kladných a celých hodnot mezi 0 a n-1, například:
-Když n = 1, pak ℓ = 0 a existuje pouze jedna podúroveň.
-Pokud n = 2, pak ℓ se může rovnat 0 nebo 1, takže máme dvě podúrovně.
-A pokud n = 3, pak ℓ předpokládá hodnoty 0, 1 a 2 a existují 3 podúrovně.
Takto lze pokračovat donekonečna, i když, jak již bylo řečeno, v praxi n stoupne až na 8. Podúrovně jsou označeny písmeny: s, p, d, F Y G a zvyšují energii.

Magnetické kvantové číslo mℓ
Toto číslo rozhoduje o orientaci orbitu v prostoru a jeho hodnota závisí na hodnotě ℓ.
Pro dané ℓ existují (2ℓ + 1) celočíselné hodnoty m ℓ, které odpovídají příslušným orbitálům. Tyto jsou:
-ℓ, (- ℓ + 1),… 0,… (+ ℓ -1), + ℓ.
Příklad
Pokud n = 2, víme, že ℓ = 0 a ℓ = 1, pak m ℓ nabývá následujících hodnot:
-Pro ℓ = 0: m ℓ = 0.
-Pro ℓ = 1: m ℓ = -1, m ℓ = 0, m ℓ = +1
Okruh n = 2 má dvě podúrovně, první s n = 2, ℓ = 0 a m ℓ = 0. Pak máme druhou úroveň: n = 2, ℓ = 1, se 3 orbitaly:
- n = 2, ℓ = 1, m ℓ = -1
- n = 2, ℓ = 1, m ℓ = 0
- n = 2, ℓ = 1, m ℓ = +1
Tyto tři orbitaly mají stejnou energii, ale odlišnou prostorovou orientaci.
Spin kvantové číslo ms
Při řešení Schrödingerovy rovnice ve třech rozměrech se objeví již popsaná čísla. U vodíku je však pozorována ještě jemnější struktura, kterou tato čísla nestačí vysvětlit.
Z tohoto důvodu v roce 1921 další fyzik, Wolfgang Pauli, navrhl existenci čtvrtého čísla: číslo rotace ms, který nabývá hodnot + ½ nebo -½.
Toto číslo popisuje velmi důležitou vlastnost elektronu, kterou je roztočit, slovo, které pochází z angličtiny roztočit (zapnout sám). A rotace zase souvisí s magnetickými vlastnostmi atomu.
Jedním ze způsobů, jak pochopit spin, je představa, že se elektron chová jako malý magnetický dipól (magnet se severním a jižním pólem) díky rotaci kolem své vlastní osy. Otáčení může být ve stejném směru jako ve směru hodinových ručiček, nebo v opačném směru.
Ačkoli Pauli navrhl existenci tohoto čísla, výsledky experimentu, který provedli Otto Stern a Walter Gerlach v roce 1922, to již očekávali..
Tito vědci dokázali rozdělit paprsek atomů stříbra na dva použitím nerovnoměrného magnetického pole.
Hodnota ms nezávisí na n, ℓ a m ℓ. V grafické podobě je to znázorněno šipkou: šipka nahoru označuje otáčení ve směru hodinových ručiček a šipka dolů označuje otáčení proti směru hodinových ručiček..
Princip vyloučení Pauli
Chování elektronů v atomu je shrnuto v Pauliho vylučovacím principu, který uvádí, že dva elektrony v atomu nemohou existovat ve stejném kvantovém stavu.
Proto každý elektron musí mít jinou množinu kvantových čísel n, ℓ, m ℓ a ms.
Důležitost kvantových čísel a tohoto principu spočívá v pochopení vlastností prvků v periodické tabulce: elektrony jsou uspořádány ve vrstvách podle n a poté v dílčích vrstvách podle ℓ a zbytku čísel.
Reference
- Alonso, M. 1971. Kvantové a statistické základy. Meziamerický vzdělávací fond.
- Bauer, W. 2011. Fyzika pro inženýrství a vědy. Svazek 1. Mc Graw Hill.
- Chang, R. 2013. Chemistry. 11. Edice. Mc Graw Hill Education.
- Eisberg-Resnick. 1989. Kvantová fyzika. Limusa - Wiley.
- Giambattista, A. 2010. Fyzika. 2. místo Ed. McGraw Hill.
- Rex, A. 2011. Základy fyziky. Pearson.
- Tippens, P. 2011. Fyzika: koncepty a aplikace. 7. vydání. Mcgraw kopec.



Zatím žádné komentáře