
Vzory stojatých vln, charakteristiky, typy, příklady
The stojaté vlny Jsou to vlny, které se šíří na omezeném médiu, které přicházejí a přicházejí v části vesmíru, na rozdíl od cestujících vln, které se při šíření vzdalují od zdroje, který je vytvořil, a nevracejí se k němu.
Jsou základem zvuků produkovaných v hudebních nástrojích, protože snadno vznikají v pevných strunách, buď na jednom konci, nebo na obou koncích. Jsou také vytvářeny v těsných membránách, jako jsou bubny nebo uvnitř trubek a struktur, jako jsou mosty a budovy..
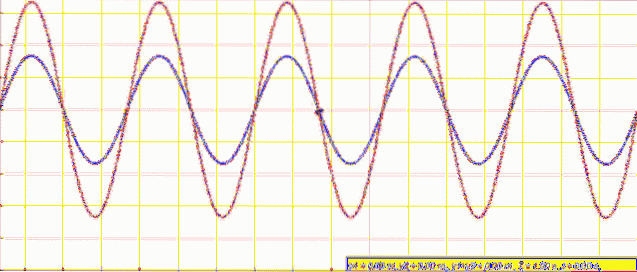
Když máte na obou koncích pevnou strunu, například kytaru, vytvoří se vlny se stejnou amplitudou a frekvencí, které se pohybují v opačných směrech a spojují se, aby vytvořily jev zvaný rušení.
Pokud jsou vlny ve fázi, vrcholy a údolí jsou zarovnány a výsledkem je vlna s dvojnásobnou amplitudou. V takovém případě mluvíme o konstruktivním rušení.
Pokud jsou ale rušivé vlny mimo fázi, vrcholy jedné se setkávají s údolími ostatních a výsledná amplituda je nulová. Jde pak o destruktivní interference.
Rejstřík článků
- 1 Vzorce a rovnice
- 1.1 Matematické vyjádření stojaté vlny
- 2 Umístění uzlů a břicha
- 2.1 Normální režimy na provázku
- 2.2 Rychlost a frekvence
- 3 Charakteristiky stojatých vln
- 4 typy
- 4.1 Stojaté vlny v jedné dimenzi
- 4.2 Stojící vlny ve dvou a třech rozměrech
- 5 Příklady stojatých vln
- 5.1 Pevná lana
- 5.2 Hudební nástroje
- 5.3 Budovy a mosty
- 5.4 Seiches
- 5.5 Akvária
- 6 Cvičení vyřešeno
- 6.1 Řešení a
- 6.2 Řešení b
- 6.3 Řešení c
- 7 Reference
Vzorce a rovnice
Hlavními prvky vlny, které ji představují v prostoru a čase, jsou její amplituda A, její vlnová délka λ a jeho úhlová frekvence ω.
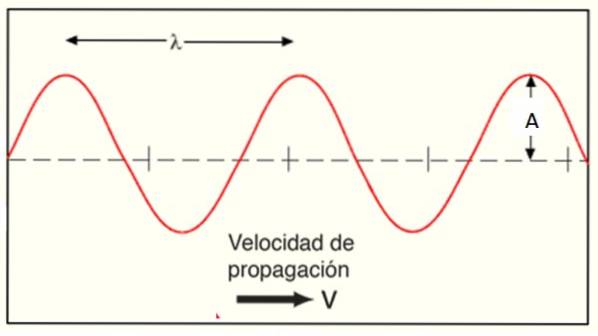
V matematické reprezentaci se dává přednost použití k, než číslo vlny nebo počet vln na jednotku délky. Proto je definována vlnovou délkou λ, což je vzdálenost mezi dvěma údolími nebo dvěma hřebeny:
k = 2π / λ
Zatímco úhlová frekvence se vztahuje k období nebo trvání úplné oscilace, jako například:
ω = 2π / T
A také frekvence f je dána vztahem:
f = ω / 2π
Proto:
f = 1 / T.
Také vlny se pohybují rychlostí proti podle:
v = λ.f
Matematické vyjádření stojaté vlny
Matematicky můžeme vlnu vyjádřit pomocí funkce sinus nebo kosinus. Předpokládejme, že máme vlny stejné amplitudy A, vlnové délky λ a frekvence ω, které se šíří podél řetězce a v opačných směrech:
Y1 = Hřích (kx - ωt)
Ydva = Hřích (kx + ωt)
Když je přidáme, najdeme výslednou vlnu aR:
YR = a1 + Ydva = A sin (kx - ωt) + A sin (kx + ωt)
K nalezení součtu existuje trigonometrická identita:
sin α + sin β = 2 sin (α + β) / 2. cos (α - β) / 2
Podle této identity je výsledná vlna yR Zůstává:
YR = [2A sin kx]. cos ωt
Umístění uzlů a břicha
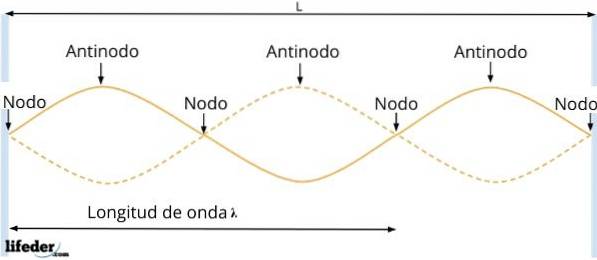
Výsledná vlna má amplitudu A.R = 2Asen kx, což závisí na poloze částice. Pak v bodech, pro které sin kx = 0, zmizí amplituda vlny, to znamená, že nedojde k žádné vibraci.
Jedná se o tyto body:
kx = π, 2π, 3π…
Protože k = 2 π / λ:
(2 π / λ) x = π, 2π, 3π…
x = λ / 2, λ, 3λ / 2 ...
V těchto bodech dochází k ničivému rušení a je vyvolán uzly. Jsou odděleny vzdáleností rovnou λ / 2, jak je odvozeno z předchozího výsledku.
A mezi dvěma po sobě následujícími uzly jsou antinody nebo břicha, ve kterém je amplituda vlny maximální, protože tam dochází ke konstruktivnímu rušení. Vyskytují se, když:
sin kx = ± 1
kx = ± π / 2, 3π / 2, 5π / 2…
Opět k = 2 π / λ a poté:
x = λ / 4, 3λ / 4, 5λ / 4,…
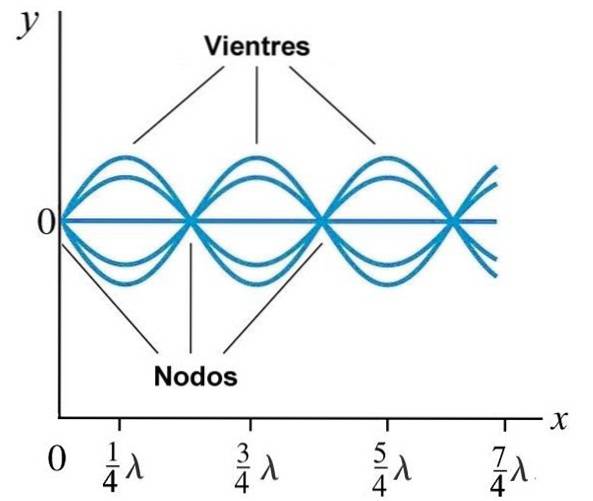
Normální režimy na provázku
Okrajové podmínky v řetězci určují, jaké jsou vlnové délky a frekvence. Pokud je řetězec délky L fixní na obou koncích, nemůže vibrovat s žádnou frekvencí, protože body, kde je řetězec fixován, jsou již uzly.
Dále je vzdálenost mezi sousedními uzly λ / 2 a mezi uzlem a břichem je λ / 4, tímto způsobem se vytvářejí stacionární vlny pouze pro určité vlnové délky: ty, ve kterých celé číslo n λ / 2 zapadá do:
(λ / 2) = L, s n = 1, 2, 3, 4 ... .
Proto:
λ = 2L / n
Harmonické
Různé hodnoty, které λ nabývá, se nazývají harmonické. Máme tedy:
-První harmonická: λ = 2L
-Druhá harmonická: λ = L
-Třetí harmonická: λ = 2 L / 3
-Čtvrtá harmonická: λ = L / 2
A tak dále.
Rychlost a frekvence
I když se stojatá vlna nejeví jako pohyblivá, rovnice stále platí:
v = λ. F
Proto:
v = (2L / n). F
f = nv / 2 l
Nyní lze ukázat, že rychlost, s jakou se vlna pohybuje v řetězci, závisí na napětí T v něm a jeho lineární hustotě hmotnosti μ (hmotnost na jednotku délky) jako:

Proto:

Charakteristika stojatých vln
-Když jsou vlny stacionární, výsledná vlna se nešíří stejně jako její složky, které přecházejí z jedné strany na druhou. Existují body, kde y = 0, protože zde nejsou žádné vibrace: uzly, jinými slovy amplituda AR stane se nula.
-Matematické vyjádření stojaté vlny se skládá z produktu prostorové části (která závisí na souřadnici x nebo prostorových souřadnicích) a časové části.
-Mezi uzly výsledná černá vlna osciluje na jednom místě, zatímco vlny procházející z jedné strany na druhou jsou tam mimo fázi..
-Energie se nepřenáší přímo v uzlech, protože je úměrná druhé mocnině amplitudy, ale je zachycena mezi uzly.
-Vzdálenost mezi sousedními uzly je polovina vlnové délky.
-Body, ve kterých je akord fixován, se také považují za uzly..
Typy
Stojící vlny v jedné dimenzi
Vlny v pevném řetězci jsou příklady stojatých vln v jedné dimenzi, jejichž matematický popis jsme nabídli v předchozích částech..
Stojící vlny ve dvou a třech rozměrech
Stojaté vlny lze také prezentovat ve dvou a tří dimenzích, jejichž matematický popis je o něco složitější.
Příklady stojatých vln
Pevná lana
-Lano upevněné na jednom konci, které osciluje ručně nebo pístem na druhém, vytváří podélné délky stojatých vln.
Hudební nástroje

-Hra na strunné nástroje, jako je kytara, harfa, housle a klavír, také vytváří stojaté vlny, protože mají struny přizpůsobené různým napětím a upevněné na obou koncích.
Stojaté vlny se také vytvářejí v trubicích se vzduchem, jako jsou trubice orgánů..
Budovy a mosty
Stojaté vlny vznikají ve strukturách, jako jsou mosty a budovy. Pozoruhodný byl případ visutého mostu Tacoma Narrows poblíž města Seattle ve Spojených státech. Krátce po slavnostním otevření v roce 1940 se tento most zhroutil kvůli stojatým vlnám vytvořeným uvnitř větrem..
Frekvence větru byla spárována s přirozenou frekvencí mostu, čímž se v něm vytvořily stojaté vlny, které rostly v amplitudě, dokud se most nezhroutil. Tento jev je známý jako rezonance.
Seiches
V přístavech se vyskytuje velmi zvědavý jev seiche, ve kterém mořské vlny produkují velké oscilace. To je způsobeno skutečností, že vody v přístavu jsou zcela uzavřené, ačkoli oceánské vody čas od času pronikají vchodem do přístavu..
Přístavní vody se pohybují svou vlastní frekvencí, stejně jako oceánské. Pokud se obě vody rovnají jejich frekvencím, vzniká rezonancí velká stojatá vlna, jak se to stalo u mostu Tacoma..
The seiches Mohou se také vyskytovat v jezerech, nádržích, bazénech a jiných vodních plochách s omezeným povrchem..
Akvária
V akváriu neseném člověkem mohou být vytvářeny stojaté vlny, pokud se frekvence, s níž osoba kráčí, rovná frekvenci kývání vodou.
Cvičení vyřešeno
Kytarová struna má L = 0,9 ma lineární hmotnostní hustotu μ = 0,005 kg / m. Je vystaven 72 N napětí a jeho režim vibrací je ten, který je znázorněn na obrázku, s amplitudou 2A = 0,5 cm.
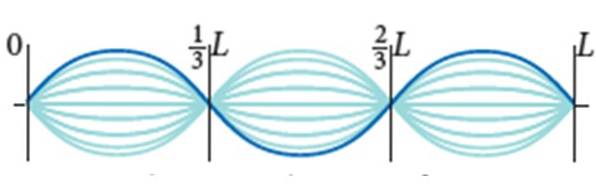
Nalézt:
a) Rychlost šíření
b) Vlnová frekvence
c) Odpovídající rovnice stojatých vln.
Řešení
Přes:

Je získán;
v = [72 N / (0,005 kg / m)]1/2 = 120 m / s.
Řešení b
Vzdálenost mezi dvěma sousedními uzly je λ / 2, proto:
(2/3) L - (1/3) L = λ / 2
(1/3) L = λ / 2
λ = 2L / 3 = 2 x 0,90 m / 3 = 0,60 m.
Protože v = λ.f
f = (120 m / s) / 0,60 m = 200 s-1= 200 Hz.
Řešení c
Rovnice je:
YR = [2A sin kx]. cos ωt
Musíme nahradit hodnoty:
k = 2π / λ = k = 2π / 0,60 m = 10 π / 3
f = ω / 2π
ω = 2π x 200 Hz = 400 π Hz.
Amplituda 2A je již dána prohlášením:
2A = 0,5 cm = 5 x 10 -3 m.
Proto:
YR = 5 x 10 -3 m. sin [(10π / 3) x]. cos (400πt) =
= 0,5 cm. sin [(10π / 3) x]. cos (400πt)
Reference
- Bauer, W. 2011. Fyzika pro inženýrství a vědy. Svazek 1. Mc Graw Hill.
- Figueroa, D. (2005). Série: Fyzika pro vědu a techniku. Svazek 7. Vlny a kvantová fyzika. Upravil Douglas Figueroa (USB).
- Giancoli, D. 2006. Fyzika: Principy s aplikacemi. 6.. Hala Ed Prentice.
- Serway, R., Jewett, J. (2008). Fyzika pro vědu a techniku. Svazek 1. 7. Ed. Cengage Learning.
- Tipler, P. (2006) Fyzika pro vědu a technologii. 5. vyd. Svazek 1. Redakční reverté.
- Wikipedia. Seiche. Obnoveno z: es.wikipedia.org.



Zatím žádné komentáře