The lineární vlny jsou ty, ve kterých je použitelný princip superpozice, tj. ty, ve kterých lze dosáhnout tvaru vlny a jejího časoprostorového vývoje jako součet základních řešení, například harmonického typu. Ne všechny vlny splňují princip superpozice, ty, které ji nesplňují, se nazývají nelineární vlny.
Název "lineární" pochází ze skutečnosti, že lineární vlny vždy uspokojují diferenciální rovnici v parciálních derivacích, ve které jsou všechny termíny, které zahrnují závislou proměnnou nebo její deriváty, zvýšeny na první mocninu.
Na druhé straně nelineární vlny uspokojují vlnové rovnice, které mají kvadratické členy nebo vyšší stupně v závislé proměnné nebo v jejích derivátech.
Lineární vlny jsou někdy zaměňovány s podélnými vlnami, což jsou ty, ve kterých dochází k vibracím ve stejném směru šíření, jako zvukové vlny.
Ale podélné vlny, stejně jako příčné vlny, mohou být zase lineární nebo nelineární, mimo jiné v závislosti na amplitudě počátečního rušení a prostředí, ve kterém se šíří..
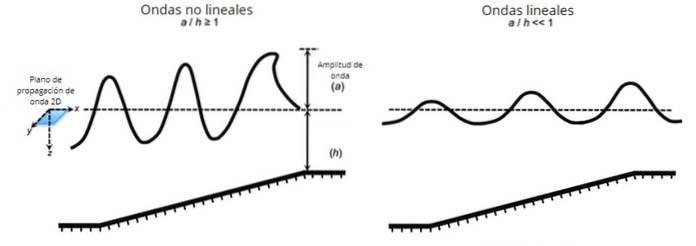
Obecně se stává, že když je počáteční porucha malá amplituda, rovnice, která popisuje šíření vlny, je lineární nebo může být linearizována určitými aproximacemi, i když tomu tak není vždy..
Rejstřík článků
V lineárním médiu může být křivka omezená v prostoru a čase reprezentována součtem vlnových funkcí sinusového nebo kosinového typu různých frekvencí a vlnových délek pomocí Fourierovy řady.
Lineární vlny vždy měly asociovanou diferenciální rovnici lineárního typu, jejíž řešení představuje předpověď toho, jaká bude narušení v pozdějších instancích počáteční poruchy lokalizované prostorově v počátečním okamžiku.
Klasická lineární vlnová rovnice v jedné prostorové dimenzi, jejíž řešení jsou lineární vlny, je:
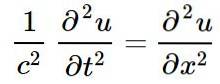
Ve výše uvedené rovnici nebo představuje narušení určité fyzické veličiny v poloze X a okamžitě t, a to nebo je funkce X Y t:
u = u (x, t)
Například pokud se jedná o zvukovou vlnu ve vzduchu, nebo může představovat změnu tlaku vzhledem k jeho hodnotě bez rušení.
V případě elektromagnetické vlny u představuje elektrické pole nebo magnetické pole oscilační kolmo ke směru šíření.
V případě napnutého lana, nebo představuje příčný posun vzhledem k rovnovážné poloze lana, jak je znázorněno na následujícím obrázku:
Pokud existují dvě nebo více řešení lineární diferenciální rovnice, pak každé řešení vynásobené konstantou bude řešením a stejně tak i jejich součet.
Na rozdíl od nelineárních rovnic lineární vlnové rovnice připouštějí harmonická řešení typu:
nebo1= A⋅sen (k⋅x - ω⋅t) Y nebodva= A⋅sen (k⋅x + ω⋅t)
To lze ověřit jednoduchou substitucí v lineární vlnové rovnici.
První řešení představuje pohybující se vlnu pohybující se doprava, zatímco druhé řešení nalevo rychle c = ω / k.
Harmonická řešení jsou charakteristická pro lineární vlnové rovnice.
Na druhou stranu je lineární kombinace dvou harmonických řešení také řešením lineární vlnové rovnice, například:
u = A1 cos (k1⋅x - ω1)T) + Adva sen (kdva⋅x - ωdva)T) je řešení.
Nejrelevantnější charakteristikou lineárních vln je to, že jakýkoli tvar vlny, bez ohledu na to, jak složitý, lze získat součtem jednoduchých harmonických vln v sinu a kosinu:
u (x, t) = A0 + ∑n NAn cos (kn⋅x - ωn)T) + ∑m Bm sen (km⋅x - ωm)T).
V klasické lineární vlnové rovnici, C představuje rychlost šíření pulzu.
V případech, kdy C je konstantní hodnota, například elektromagnetické vlny ve vakuu, pak puls v počátečním okamžiku t = 0 Tvar f (x) spready podle:
u (x, t) = f (x - c⋅t)
Bez utrpení jakéhokoli zkreslení. Když k tomu dojde, médium je považováno za nedisperzní..
V disperzním médiu však rychlost šíření c může záviset na vlnové délce λ, to znamená: c = c (λ).
Elektromagnetické vlny jsou disperzní při cestování materiálem. Rovněž povrchové vlny vody cestují různými rychlostmi v závislosti na hloubce vody.
Rychlost, s níž harmonická vlna typu A⋅sen (k⋅x - ω⋅t) to je ω / k = c y se nazývá fázová rychlost. Pokud je médium disperzní, pak C je funkcí čísla vlny k: c = c (k), kde k souvisí s vlnovou délkou od k = 2π / λ.
Vztah mezi frekvencí a vlnovou délkou se nazývá disperzní poměr, než vyjádřeno úhlovou frekvencí ω a číslo vlny k to je: ω = c (k) ⋅k.
Některé charakteristické disperzní vztahy lineárních vln jsou následující:
Ve vlnách oceánu, kde je vlnová délka (vzdálenost mezi hřebeny) mnohem větší než hloubka H, ale protože jeho amplituda je mnohem menší než hloubka, rozptylový vztah je:
ω = √ (gH) ⋅k
Odtud se usuzuje, že se šíří konstantní rychlostí √ (gH) (nedisperzní médium).
Ale vlny ve velmi hlubokých vodách jsou disperzní, protože jejich disperzní poměr je:
ω = √ (g / k) ⋅k
To znamená, že fázová rychlost ω / k je proměnná a závisí na počtu vln, a tedy na vlnové délce vlny.
Pokud se dvě harmonické lineární vlny překrývají, ale postupují různými rychlostmi, skupinová rychlost (tj. Vlnového paketu) neodpovídá fázové rychlosti.
Rychlost skupiny protiG je definována jako derivace frekvence vzhledem k počtu vln v disperzním vztahu: protiG = ω '(k).
Následující obrázek ukazuje superpozici nebo součet dvou harmonických vln nebo1= A⋅sen (k1⋅x - ω1)T) Y nebodva= A⋅sen (kdva⋅x - ωdva)T) cestování různými rychlostmi proti1= ω1/ k1 Y protidva= ωdva/ kdva. Všimněte si, jak se skupinová rychlost liší od fázové rychlosti, v tomto případě je skupinová rychlost ∆ω / ∆k.
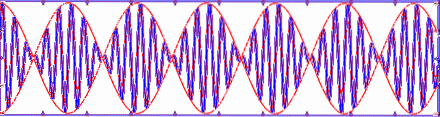
V závislosti na disperzním poměru se může dokonce stát, že fázová rychlost a skupinová rychlost v lineárních vlnách mají opačné směry..
Elektromagnetické vlny jsou lineární vlny. Jeho vlnová rovnice je odvozena z rovnic elektromagnetismu (Maxwellovy rovnice), které jsou také lineární.
Je to rovnice, která popisuje dynamiku částic na atomovém měřítku, kde jsou relevantní vlnové charakteristiky, například elektrony v atomu.
Takže „elektronová vlna“ nebo vlnová funkce, jak se jí také říká, je lineární vlna.
Lineární vlny jsou také ty, ve kterých je amplituda mnohem menší než vlnová délka a vlnová délka mnohem větší než hloubka. Vlny v hluboké vodě se řídí lineární teorií (známou jako teorie vzdušných vln).
Vlna, která se blíží ke břehu a tvoří charakteristický curlingový hřeben (a který surfaři milují), je nelineární vlna..
Protože zvuk je malou poruchou atmosférického tlaku, považuje se za lineární vlnu. Typickým příkladem nelineární vlny jsou však rázová vlna z exploze nebo vlnová fronta z nadzvukového letadla..
Vlny, které se šíří napnutým lanem, jsou lineární, pokud je počáteční pulzace malá amplituda, to znamená, že není překročena mez pružnosti lana..
Lineární vlny v strunách se odrážejí na jejich koncích a překrývají se, čímž vznikají stojaté vlny nebo vibrační režimy, které dávají harmonické a subharmonické tóny charakteristické pro strunné nástroje..
Zatím žádné komentáře