
Matematické vyjádření a příklady jednorozměrných vln
The jednorozměrné vlny Jsou to ty, které se šíří v jednom směru bez ohledu na to, zda vibrace probíhá ve stejném směru šíření nebo ne. Dobrým příkladem je vlna, která prochází napnutou strunou, jako je kytara..
V ploché vlně přejít, částice vibrují ve svislém směru (pohybují se nahoru a dolů, viz červená šipka na obrázku 1), ale je to jednorozměrné, protože rušení se šíří pouze jedním směrem podle žluté šipky.

Jednorozměrné vlny se v každodenním životě objevují poměrně často. Následující část popisuje některé jejich příklady a také vlny, které nejsou jednorozměrné, aby bylo možné jasně stanovit rozdíly.
Rejstřík článků
- 1 Příklady jednorozměrných vln a ne-jednorozměrných vln
- 1.1 Jednorozměrné vlny
- 1.2 Nerozměrné vlny
- 2 Matematické vyjádření jednorozměrné vlny
- 2.1 Jednorozměrná vlnová rovnice
- 2.2 Pracoval příklad
- 3 Odkazy
Příklady jednorozměrných vln a ne-jednorozměrných vln
Jednorozměrné vlny
Zde je několik příkladů jednorozměrných vln, které lze snadno pozorovat:
- Pulz zvuku, který prochází přímým pruhem, protože se jedná o poruchu, která šíří celou délku pruhu.
- Vlna procházející vodním kanálem, i když posunutí vodní hladiny není rovnoběžné s kanálem.
- Vlny, které se šíří na povrchu nebo trojrozměrným prostorem, mohou být také jednorozměrné, pokud jsou jejich vlnové fronty rovinami navzájem rovnoběžnými a pohybují se pouze jedním směrem..
Non-jednorozměrné vlny
Příklad ne-jednorozměrné vlny se nachází ve vlnách, které se tvoří na hladké vodní hladině, když spadne kámen. Je to dvourozměrná vlna s válcovou vlnovou čárou.

Dalším příkladem jednorozměrné vlny je zvuková vlna, kterou petarda generuje výbuchem v určité výšce. Toto je trojrozměrná vlna se sférickými vlnovými frontami.
Matematické vyjádření jednorozměrné vlny
Nejobecnější způsob vyjádření jednorozměrné vlny, která se šíří bez útlumu v kladném směru osy X as rychlostí proti je matematicky:
y (x, t) = f (x - v.t)
V tomto výrazu Y představuje poruchu v poloze X Okamžitě t. Tvar vlny je dán funkcí F. Například vlnová funkce zobrazená na obrázku 1 je: y (x, t) = cos (x - v t) a vlnový obraz odpovídá okamžiku t = 0.
Taková vlna, popsaná kosinusovou nebo sínusovou funkcí, se nazývá harmonická vlna. Ačkoli to není jediný tvar vlny, který existuje, je nanejvýš důležitý, protože jakoukoli jinou vlnu lze reprezentovat jako superpozici nebo součet harmonických vln. Jde o známé Fourierova věta, tak se používá k popisu signálů všeho druhu.
Když se vlna pohybuje v záporném směru osy x, jednoduše se změní proti pro -proti v argumentu opouští:
y (x, t) = g (x + v t)
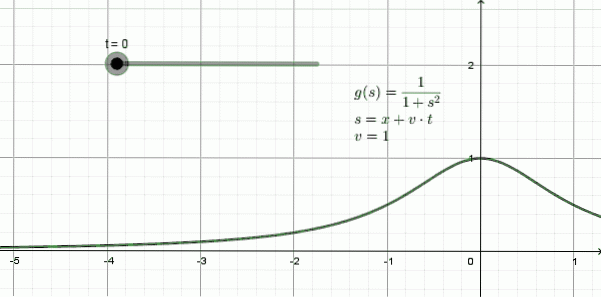
Obrázek 3 ukazuje animaci vlny pohybující se doleva: jedná se o tvar zvaný funkce lorentziana a ona matematický výraz je:
y (x, t) = 1 / (1 + (x + 1⋅t)dva
V tomto příkladu je rychlost šíření v = 1, -jedna jednotka prostoru pro každou jednotku času-.
Jednorozměrná vlnová rovnice
Vlnová rovnice je parciální derivační rovnice, jejímž řešením je samozřejmě vlna. Stanovuje matematický vztah mezi prostorovou částí a její časovou částí a má formu:

Pracoval příklad
Toto je obecný výraz y (x, t) pro harmonickou vlnu:
y (x, t) = A⋅cos (k⋅x ± ω⋅t + θo)
a) Popište fyzický význam parametrů A, k, ω Y θo.
b) Jaký význam mají znaménka ± v kosinusovém argumentu?
c) Ověřte, že daný výraz je skutečně řešením vlnové rovnice z předchozí části a vyhledejte rychlost proti propagace.
Řešení)
Charakteristiky vlny se nacházejí v následujících parametrech:
-NA představuje amplituda nebo „výška vlny“.
-Co je uvnitř číslo vlny a souvisí s vlnovou délkou λ přes k = 2π / λ.
-ω je fúhlová frekvence a souvisí s doba T kmitání vln o
ω = 2π / T.
-θo je úvodní fáze, který souvisí s počátečním bodem vlny.
Řešení b)
Negativní znaménko je přijato, pokud se vlna pohybuje v kladném směru osy X a kladné znaménko jinak..
Řešení c)
Ověřte, že daný výraz je řešením vlnové rovnice je jednoduchá: parciální derivace funkce je převzata y (x, t) s ohledem na x dvakrát, částečně znovu derivovat s ohledem na t dvakrát, a poté zkombinovat oba výsledky k získání rovnosti:
Druhá derivace vzhledem k x: ∂dvay / ∂xdva= -Kdva. NA⋅cos (k⋅x ± ω⋅t + θo)
Druhá derivace vzhledem k t: ∂dvay / ∂tdva= -Ωdva. NA⋅cos (k⋅x ± ω⋅t + θo)
Tyto výsledky jsou nahrazeny vlnovou rovnicí:
-kdva. NA⋅cos (k⋅x ± ω⋅t + θo) = (1 / vdva) (-ωdva. NA⋅cos (k⋅x ± ω⋅t + θo))
Tak moc NA protože kosinus jsou zjednodušeny, protože se objevují na obou stranách rovnosti a argument kosinu je stejný, proto se výraz redukuje na:
-kdva = (1 / vdva) (-ωdva)
Což umožňuje získat rovnici pro proti ve smyslu ω Y k:
protidva = ωdva / kdva
v = ± ω / k
Reference
- E-vzdělávací. Rovnice jednorozměrných harmonických vln. Obnoveno z: e-ducativa.catedu.es
- Roh fyziky. Vlnové třídy. Obnoveno z: fisicaparatontos.blogspot.com.
- Figueroa, D. 2006. Vlny a kvantová fyzika. Série: Fyzika pro vědu a techniku. Upravil Douglas Figueroa. Univerzita Simona Bolívara. Caracas Venezuela.
- Fyzikální laboratoř. Vlnový pohyb. Obnoveno z: fisicalab.com.
- Peirce, A. Přednáška 21: Jednorozměrná vlnová rovnice: D'Alembertovo řešení. Obnoveno z: ubc.ca.
- Vlnová rovnice. Obnoveno z: en.wikipedia.com


Zatím žádné komentáře